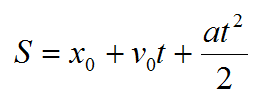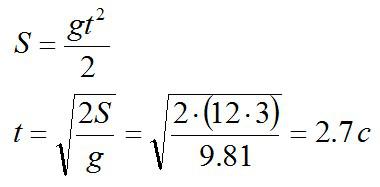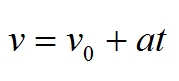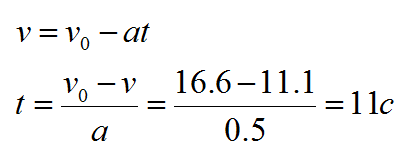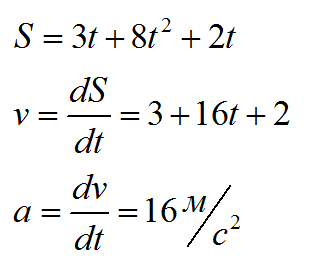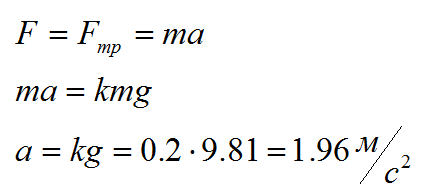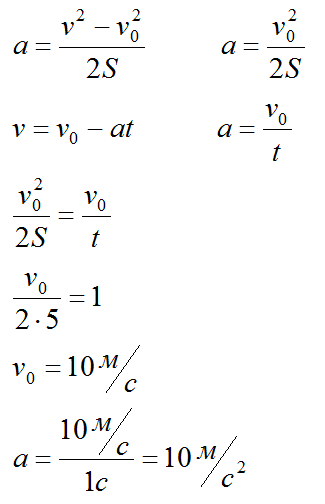Мотогонщик стартует и разгоняется с постоянным ускорением a известно что за первую
Решение задач по теме «Ускорение. Скорость при прямолинейном движении с постоянным ускорением»
План-конспект урока по теме «Решение задач по теме « Ускорение. Скорость при прямолинейном движении с постоянным ускорением »»
Тема: Решение задач по теме « Ускорение. Скорость при прямолинейном движении с постоянным ускорением »»
Образовательная : формирование практических умений по решению задач на тему « Ускорение. Скорость при прямолинейном движении с постоянным ускорением »;
Развивающая : совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), развивать познавательный интерес;
Воспитательная : прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.
Тип урока: обобщение и систематизация знаний
Оборудование и источники информации:
Исаченкова, Л. А. Физика : учеб. для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2015
Карточки с условиями задач
Организационный момент (5 мин)
Актуализация опорных знаний (5 мин)
Закрепление знаний(30 мин)
Здравствуйте, садитесь! (Проверка присутствующих). Сегодня на уроке мы должны научиться решать задачи по теме « Ускорение. Скорость при прямолинейном движении с постоянным ускорением ». А это значит, что Тема урока : Решение задач по теме « Ускорение. Скорость при прямолинейном движении с постоянным ускорением »
Актуализация опорных знаний
Что называется ускорением?
Как зависит скорость от времени при движении с постоянным ускорением?
А сейчас перейдем к решению задач (приложение 1)
№ 2. Автомобиль движется в северном направлении со скоростью 90 Найдите модуль и направление его постоянного ускорения при торможении перед светофором за 4 с. Рассчитайте длину тормозного пути автомобиля.
№ 3. Санки двигались со скоростью, модуль которой и начали тормозить с постоянным ускорением, модуль которого Определите промежуток времени, в течение которого останавливались санки.
Итак, подведем итоги. Что вы сегодня узнали на уроке?
Организация домашнего задания
Сегодня на уроке я узнал…
Знания, которые я получил на уроке, пригодятся
Решение задач по теме «Ускорение. Скорость при прямолинейном движении с постоянным ускорением»
№ 2. Автомобиль движется в северном направлении со скоростью 90 Найдите модуль и направление его постоянного ускорения при торможении перед светофором за 4 с. Рассчитайте длину тормозного пути автомобиля.
№ 3. Санки двигались со скоростью, модуль которой и начали тормозить с постоянным ускорением, модуль которого Определите промежуток времени, в течение которого останавливались санки.
Задачи на равноускоренное движение: примеры решения задач по кинематике
При решении задач на равноускоренное движение не обойтись без формул кинематики и второго закона Ньютона. Рекомендуем сначала изучить теорию по этим разделам, а уже потом приступать к практике.
Больше полезных сведений и ежедневная интересная рассылка – на нашем телеграм-канале, присоединяйтесь!
Равноускоренное движение: определение и примеры
Равноускоренное движение – это движение с меняющейся скоростью, но постоянным ускорением (a=const).
Самый простой случай такого движения – равноускоренное прямолинейное движение.
Вот типичные примеры равноускоренного движения:
Вопросы с ответами на равноускоренное движение
Вопрос 1. График движения представляет собой прямую линию. Является ли движение тела равноускоренным?
Ответ: да. Если график представляет собой кривую, то ускорение тела меняется со временем. Равномерное движение, которое также описывается прямой – частный случай равноускоренного движения с нулевым ускорением. Перемещение при равноускоренном движении численно равно площади трапеции, ограниченной осями координат и графиком.
Вопрос 2. Тело равномерно движется по окружности. Как направлено ускорение?
Ответ: перпендикулярно телу. В общем случае при криволинейном движении ускорение имеет две составляющие: нормальную (центростремительное ускорение) и тангенциальную, направленную по касательной к скорости. Тангенциальное ускорение при равномерном движении по окружности равно нулю.
Вопрос 3. Является ли ускорение свободного падения постоянным ускорением?
Ответ: да, является.
Вопрос 4. Может ли тело иметь нулевую скорость и ненулевое ускорение?
Ответ: да, может. После того, как скорость станет равна нулю, тело начнет двигаться в другом направлении.
Вопрос 5. Что такое ускорение?
Ответ: Векторная физическая величина, характеризующая изменение скорости за единицу времени. При равноускоренном движении скорость меняется одинаково за равные промежутки времени.
Задачи на равноускоренное движение
Сначала обратимся к уже приведенным примерам.
Задача №1. Равноускоренное движение
Условие
Рояль роняют с 12 этажа с нулевой начальной скоростью. За какое время он долетит до земли? Один этаж имеет высоту 3 метра, сопротивлением воздуха принебречь.
Решение
Известно, что рояль движется с ускорением свободного падения g. Применим формулу для пути из кинематики:
Начальная скорость равна нулю, а за точку отсчета примем то место, откуда рояль начал движение вниз.
Скорость свободно падающих тел не зависит от их массы. Любое тело в поле силы тяжести Земли будет падать с одинаковым ускорением. Этот факт был экспериментально установлен Галилео Галилеем в его знаменитых экспериментах со сбрасыванием предметов с Пизанской башни.
Задача №2. Равноускоренное движение
Условие
Автобус ехал со скоростью 60 км/ч и начал тормозить на светофоре с ускорением 0,5 метра на секунду в квадрате. Через сколько секунд его скорость станет равной 40 км/ч?
Решение
Вспоминаем формулу для скорости:
Начальная скорость дана в условии, но автобус тормозит, а значит, векторы скорости и ускорения направлены в противоположные стороны. В проекции на горизонтальную ось ускорение будем записывать со знаком минус:
Обязательно переводите величины в систему СИ.Чтобы перевести километры в час в метры в секунду нужно значение скорости в километрах в час сначала умножить на 1000, а потом разделить на 3600.
Задача №3. Нахождение ускорения
Условие
Тело движется по закону S(t)=3t+8t^2+2t. Каково ускорение тела?
Решение
Вспоминаем, что скорость – это производная пути по времени, а ускорение – производная скорости:
Ответ: 16 метров на секунду в квадрате.
При решении физических задач не обойтись без знания производной.
Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задача №4. Нахождение ускорения при равноускоренном движении
Условие
Грузовик разгоняется на дороге, а в кузове лежит незакрепленный груз. С каким максимальным ускорением должен разгоняться грузовик, чтобы груз не начал смещаться к заднему борту? Коэффициент трения груза о дно кузова k=0.2, g=10 м/c2
Решение
Для решения этой задачи нужно использовать второй закон Ньютона. Сила трения в данном случае равна F=kmg.
Ответ: 2 метра на секунду в квадрате.
Задача №5. Нахождение ускорения и скорости при равноускоренном движении
Условие
За пятую секунду прямолинейного движения с постоянным ускорением тело проходит путь 5 м и останавливается. Найти ускорение тела.
Решение
Конечная скорость тела v равна 0, v нулевое – скорость в конце 4-й секунды.
Ответ: 10 метров на секунду в квадрате.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис в любое время.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Прямолинейное равноускоренное движение. Ускорение, скорость, перемещение
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
1439. Мотоцикл в течение 5 с может увеличить скорость от 0 до 72 км/ч. Определите ускорение мотоцикла.
1440. Определите ускорение лифта в высотном здании, если он увеличивает свою скорость на 3,2 м/с в течение 2 с.
1441. Автомобиль, двигавшийся со скоростью 72 км/ч, равномерно тормозит и через 10 с останавливается. Каково ускорение автомобиля?
1442. Как назвать движения, при которых ускорение постоянно? равно нулю?
Равноускоренное, равномерное.
1443. Санки, скатываясь с горы, движутся равноускоренно и в конце третьей секунды от начала движения имеют скорость 10,8 км/ч. Определите, с каким ускорением движутся санки.
1445. Мотоцикл «Хонда», двигавшийся со скоростью 90 км/ч, начал равномерно тормозить и через 5 с сбросил скорость до 18 км/ч. Каково ускорение мотоцикла?
1446. Объект из состояния покоя начинает двигаться с постоянным ускорением, равным 6 • 10-3 м/с2. Определите скорость через 5 мин после начала движения. Какой путь прошел объект за это время?
1447. Яхту спускают на воду по наклонным стапелям. Первые 80 см она прошла за 10 с. За какое время яхта прошла оставшиеся 30 м, если ее движение оставалось равноускоренным?
1448. Грузовик трогается с места с ускорением 0,6 м/с2. За какое время он пройдет путь в 30 м?
1449. Электричка отходит от станции, двигаясь равноускоренно в течение 1 мин 20 с. Каково ускорение электрички, если за это время ее скорость стала 57,6 км/ч? Какой путь она прошла за указанное время?
1450. Самолет для взлета равноускоренно разгоняется в течение 6 с до скорости 172,8 км/ч. Найдите ускорение самолета. Какое расстояние прошел самолет при разгоне?
1451. Товарный поезд, трогаясь с места, двигался с ускорением 0,5 м/с2 и разогнался до скорости 36 км/ч. Какой путь он при этом прошел?
1452. От станции равноускоренно тронулся скорый поезд и, пройдя 500 м, достиг скорости 72 км/ч. Каково ускорение поезда? Определите время его разгона.
1454. Электричка, шедшая со скоростью 72 км/ч, начала тормозить с постоянным ускорением, равным по модулю 2 м/с2. Через какое время она остановится? Какое расстояние она пройдет до полной остановки?
1455. Городской автобус двигался равномерно со скоростью 6 м/с, а затем начал тормозить с ускорением, по модуля равным 0,6 м/с2. За какое время до остановки и на каком расстоянии от нее надо начать торможение?
1456. Санки скользят по ледяной дорожке с начальной скоростью 8 м/с, и за каждую секунду их скорость уменьшается на 0,25 м/с. Через какое время санки остановятся?
1457. Мотороллер, двигавшийся со скоростью 46,8 км/ч, останавливается при равномерном торможении в течение 2 с. Каково ускорение мотороллера? Каков его тормозной путь?
1458. Теплоход, плывущий со скоростью 32,4 км/ч, стал равномерно тормозить и, подойдя к пристани через 36 с, полностью остановился. Чему равно ускорение теплохода? Какой путь он прошел за время торможения?
1459. Товарняк, проходя мимо шлагбаума, приступил к торможению. Спустя 3 мин он остановился на разъезде. Какова начальная скорость товарняка и модуль его ускорения, если шлагбаум находится на расстоянии 1,8 км от разъезда?
1460. Тормозной путь поезда 150 м, время торможения 30 с. Найдите начальную скорость поезда и его ускорение.
1461. Электричка, двигавшаяся со скоростью 64,8 км/ч, после начала торможения до полной остановки прошла 180 м. Определите ее ускорение и время торможения.
1462. Аэроплан летел равномерно со скоростью 360 км/ч, затем в течение 10 с он двигался равноускоренно: его скорость возрастала на 9 м/с за секунду. Определите, какую скорость приобрел аэроплан. Какое расстояние он пролетел при равноускоренном движении?
1463. Мотоцикл, двигавшийся со скоростью 27 км/ч, начал равномерно ускоряться и через 10 с достиг скорости 63 км/ч. Определите среднюю скорость мотоцикла при равноускоренном движении. Какой путь он проехал за время равноускоренного движения?
1464. Прибор отсчитывает промежутки времени, равные 0,75 с. Шарик скатывается с наклонного желоба в течение трех таких промежутков времени. Скатившись с наклонного желоба, он продолжает двигаться по горизонтальному желобу и проходит в течение первого промежутка времени 45 см. Определите мгновенную скорость шарика в конце наклонного желоба и ускорение шарика при движении по этому желобу.
1465. Отходя от станции, поезд движется равноускоренно с ускорением 5 см/с2. По прошествии какого времени поезд приобретает скорость 36 км/ч?
1466. При отправлении поезда от станции его скорость в течение первых 4 с возросла до 0,2 м/с, в течение следующих 6 с еще на 30 см/с и за следующие 10 с на 1,8 км/ч. Как двигался поезд в течение этих 20 с?
1467. Санки, скатываясь с горы, движутся равноускоренно. На некотором участке пути скорость санок в течение 4 с возросла от 0,8 м/с до 14,4 км/ч. Определите ускорение санок.
1468. Велосипедист начинает двигаться с ускорением 20 см/с2. По истечении какого времени скорость велосипедиста будет равна 7,2 км/ч?
1469. На рисунке 184 дан график скорости некоторого равноускоренного движения. Пользуясь масштабом, данным на рисунке, определите путь, проходимый в этом движении в течение 3,5 с.
1470. На рисунке 185 изображен график скорости некоторого переменного движения. Перечертите рисунок в тетрадь и обозначьте штриховкой площадь, численно равную пути, проходимому в течение 3 с. Чему примерно равен этот путь?
1471. В течение первого промежутка времени от начала равноускоренного движения шарик проходит по желобу 8 см. Какое расстояние пройдет шарик в течение трех таких же промежутков, прошедших от начала движения?
1472. В течение 10 равных промежутков времени от начала движения тело, двигаясь равноускоренно, прошло 75 см. Сколько сантиметров прошло это тело в течение двух первых таких же промежутков времени?
1473. Поезд, отходя от станции, движется равноускоренно и в течение двух первых секунд проходит 12 см. Какое расстояние пройдет поезд в течение 1 мин, считая от начала движения?
1474. Поезд, отходя от станции, движется равноускоренно с ускорением 5 см/с2. Сколько времени потребуется для развития скорости 28,8 км/ч и какое расстояние пройдет поезд за это время?
1475. Паровоз по горизонтальному пути подходит к уклону со скоростью 8 м/с, затем движется вниз по уклону с ускорением 0,2 м/с. Определите длину уклона, если паровоз проходит его за 30 с.
1476. Начальная скорость тележки, движущейся вниз по наклонной доске, равна 10 см/с. Всю длину доски, равную 2 м, тележка прошла в течение 5 сек. Определите ускорение тележки.
1477. Пуля вылетает из ствола ружья со скоростью 800 м/с. Длина ствола 64 см. Предполагая движение пули внутри ствола равноускоренным, определите ускорение и время движения.
1478. Автобус, двигаясь со скоростью 4 м/с, начинает равномерно ускоряться на 1 м/с за секунду. Какой путь пройдет автобус за шестую секунду?
1479. Грузовик, имея некоторую начальную скорость, начал двигаться равноускоренно: за первые 5 с прошел 40 м, а за первые 10 с — 130 м. Найдите начальную скорость грузовика и его ускорение.
1480. Катер, отходя от пристани, начал равноускоренное движение. Пройдя некоторое расстояние, он достиг скорости 20 м/с. Какова была скорость катера в тот момент, когда он проплыл половину этого расстояния?
1481. Лыжник скатывается с горы с нулевой начальной скоростью. На середине горы его скорость была 5 м/с, через 2 с скорость стала 6 м/с. Считая, что она увеличивается равномерно, определите скорость лыжника через 8 с после начала движения.
1482. Автомобиль тронулся с места и двигается равноускоренно. За какую секунду от начала движения путь, пройденный автомобилем, вдвое больше пути, пройденного им в предыдущую секунду?
1483. Найдите путь, пройденный телом за восьмую секунду движения, если оно начинает двигаться равноускоренно без начальной скорости и за пятую секунду проходит путь 27 м.
1484. Провожающие стоят у начала головного вагона поезда. Поезд трогается и движется равноускоренно. За 3 с весь головной вагон проходит мимо провожающих. За какое время пройдет мимо провожающих весь поезд, состоящий из 9 вагонов?
1485. Материальная точка движется по закону x = 0,5t². Какое это движение? Каково ускорение точки? Постройте график зависимости от времени:
а) координаты точки;
б) скорости точки;
в) ускорения.
1486. Поезд остановился через 20 с после начала торможения, пройдя за это время 120 м. Определите первоначальную скорость поезда и ускорение поезда.
1487. Поезд, идущий со скоростью 18 м/с, начал тормозить, и через 15 с остановился. Считая движение поезда при торможении равнозамедленным, определите путь, пройденный поездом за эти 15 с.
1488. Постройте графики скорости равнозамедленного движения для случаев:
1) V0 = 10 м/с, а = — 1,5 м/с2;
2) V0 = 10 м/с; а = — 2 м/с2.
Масштаб в обоих случаях одинаков: 0,5 см – 1 м/с; о,5 см – 1 сек.
1489. Изобразите пройденный путь за время t на графике скорости равнозамедленного движения. Принять V0 = 10 м/с, а = 2 м/с2.
1490. Опишите движения, графики скоростей которых даны на рисунке 186, а и б.
а) движение будет равнозамедленным;
б) сначала тело будет двигаться равноускоренно, затем равномерно. На 3м участке движение будет равнозамедленное.
Мотогонщик стартует и разгоняется с постоянным ускорением a известно что за первую
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути
км:
Найдём, при каком ускорении автомобиль достигнет требуемой скорости, проехав 0,8 километра. Задача сводится к решению уравнения при известном значении длины пути
км:
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,7 километра. Задача сводится к решению уравнения при известном значении длины пути
км:
Я не понял! Этот гонщик у вас на космическом корабле что ли гоняет?
Все в порядке с ним. Выразите ускорение в метрах в секунду в квадрате, сами убедитесь.
Выразим ускорение из формулы для скорости и найдём его:
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 1,1 км. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км:
Это задание ещё не решено, приводим решение прототипа.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав один километр. Задача сводится к решению уравнения при известном значении длины пути
км: