На чем базируются построения математических и физических моделей подземная гидромеханика

Подземная гидромеханика. Физические основы подземной гидромеханики

2) Основные требования адекватности моделей реальным процессам.

3) Основное требование осреднения параметров по пространству, дающее право считать их непрерывным.

4) Почему в нефтяной гидромеханике процесс фильтрации флюидов можно считать изотермическим?

5) Назовите примеры нестационарных и стационарных процессов в нефтегазовой гидродинамике.

6) Модели флюидов по степени сжимаемости.

7) В чем отличие многофазной модели от гомогенной? Приведите примеры.

8) Определение ньютоновской и неньютоновских жидкостей. Примеры.

9) Виды моделей коллекторов с геометрической точки зрения.

10) Идеализированные модели пористых коллекторов.

11) Реологические модели горных пород.

12) Какие среды называются изотропными и анизотропными?

13) Виды пористости и их определения? Размерности.

14) Виды проницаемости и их определения? Размерности в различных системах единиц и их связь между собой.

15) Определение эффективного диаметра.

16) Что такое насыщенность и связанность? Чему равна сумма насыщенностей?

17) Удельная поверхность – определение, размерность, характерные значения для коллекторов.

4. НЕЛИНЕЙНЫЕ ЗАКОНЫ ФИЛЬТРАЦИИ

5. УСТАНОВИВШИЙСЯ ПРИТОК ЖИДКОСТИ К ГРУППЕ СКВАЖИН.

1. Интерференция скважин.

2. Принцип суперпозиции фильтрационных полей.

3. Основные формулы для расчета дебитов жидкости из залежей методом ЭГДА (метод Ю.П.Борисова).

4. Вывод уравнения притока жидкости к несовершенным скважинам.

5. Методы учета несовершенства скважин при расчете их дебита.

(для формирования экзаменационных билетов)

Источник

ГЛАВА 1. ФИЗИЧЕСКИЕ ОСНОВЫ ПОДЗЕМНОЙ ГИДРОМЕХАНИКИ

ВВЕДЕНИЕ

Подземная нефтегазовая гидромеханика (ПГМ) – наука о движении нефти, воды, газа и их смесей по коллекторам. Коллектора –это горные породы, которые могут служить хранилищами нефти, газа, воды и отдавать их при разработке. Жидкость, газ, смесь жидкости и газа, то есть всякая текучая среда, часто именуется общим термином флюид, если не ставится задача выделить характерные особенности движения данной среды.

ГЛАВА 1. ФИЗИЧЕСКИЕ ОСНОВЫ ПОДЗЕМНОЙ ГИДРОМЕХАНИКИ

Понятие о моделировании

Особенностью подземной гидромеханики является одновременное рассмотрение процессов в областях, характерные размеры которых различаются на порядки – от микрометров (размеры пор и трещин) до десятков и сотен километров (протяженность месторождений). Кроме того, неоднородность пластов (по толщине и площади) имеет характерные размеры практически любого масштаба.

Указанные неоднородности по строению залежей, а также значительная широта фациального состава коллекторов и сложный нерегулярный характер структуры порового пространства обуславливают ограниченность и приближенность сведений о пласте и флюидах, полученных в результате геологических и геофизических исследований. Таким образом, исследование пластов невозможно без абстрактного (математического) и физического (лабораторного) моделирования.

При абстрактном моделировании реальные процессы описываются некоторой математической моделью, полученной на основе осреднения характерных параметров по времени, пространству и статистической выборке. Это осреднение позволяет перейти от дискретных распределений к непрерывным и, следовательно, использовать хорошо разработанные методы механики сплошных сред и дифференциального исчисления.

Математическое моделирование предполагает использование целого ряда зависимостей, позволяющих в той или иной мере отожествить математическую модель с реальными физическими средами и процессами.

В силу разнообразия реальных сред, процессов и огромного числа взаимосвязанных факторов для получения данных зависимостей в подземной гидромеханике широко используется физическое моделирование, основанное на теории подобия.

Адекватность абстрактных и физических моделей реальным процессам требует выполнения некоторых требований при их построении:

· полнота – содержание достаточного числа признаков реального объекта;

· непротиворечивость – включенные признаки не должны противоречить друг другу;

· реализуемость – построенная математическая модель должна допускать аналитическое или численное решение, а физическая – реализацию в искусственных условиях;

· компактность и экономичность – процессы сбора информации, подготовка и реализация модели должны быть максимально просты, обозримы и экономически целесообразны.

При моделировании пластов и фильтрационных процессов необходимо помнить о принципиальной невозможности достижения точного количественного описания, и, следовательно, основная задача исследования заключается в установлении качественных закономерностей, устойчивых тенденций, а также количественных соотношений, устойчивых к вариации исходных данных. Целью моделирования является не столько точное определение всех характеристик процесса, сколько расширение той совокупности сведений, которые учитываются при выборе системы разработки или метода воздействия на пласт. При этом уточнение и коррекция данных сведений возможны только на основе анализа последующего поведения пласта. Решающую роль играет постановка задачи и такой анализ результатов ее реализации, который позволяет сделать некоторые общие заключения. Следует иметь в виду, что усложнение модели путем увеличения признаков сверх определяющих основные закономерности может привести не к увеличению точности, а к получению качественно неверных результатов.

Модели фильтрационного течения, флюидов и коллекторов

Модели флюидов

По степени сжимаемости. Природный газ способен значительно изменять свой объём при изменении давления, вода и нефть в довольно значительном диапазоне давлений (приблизительно до 20МПа) практически несжимаемы, а при высоких давлениях обладают упругими свойствами. В связи с указанными факторами различают модели сжимаемой, несжимаемой и упругой среды. Построение каждой из указанной модели требует привлечения эмпирических уравнений состояния – соотношений, связывающих изменение объёма с изменением давления.

Гомогенные и многофазные модели. В области контакта флюидов при вытеснении одного другим или при выделении одного флюида из другого в каждом микрообъёме содержится два или больше флюидов, занимающих отдельные четко различимые объёмы (пузырьки газа в жидкости, капли или плёнки в газе) и взаимодействующих на поверхностях раздела. Такие системы называют многофазными (двух, трёх и т.д.), в отличие от многокомпонентных смесей (природный газ, нефть), в которых взаимодействие происходит на молекулярном уровне, и поверхности раздела выделить нельзя. В гидродинамике такие среды называют однофазными или гомогенными.

Ньютоновские и неньютоновские жидкости. В процессе движения флюиды испытывают различные деформации (сжатие, кручение, растяжение и т.д.) при изменении нагрузки (трение соседних объёмов, внешние силы), которая, отнесённая к единице площади, получила название напряжения. Само соотношение, связывающее деформацию или скорость изменения деформации с напряжением, называется реологическим соотношением или законом. Наиболее часто, применительно к жидкостям, для описания действия касательных напряжений t_xy на сдвиговую деформацию применяют соотношение Ньютона , где u_x– скорость в направлении х;

у– направление, перпендикулярное х.

Довольно часто движение флюидов не подчиняется данному закону, например, при страгивании пластовой нефти требуется некоторое, отличное от нулевого, напряжение, чтобы разорвать образованные пластовой водой коллоидные структуры. Такие среды называются неньютоновскими, а модель – моделью неньютоновского течения.

Модели коллекторов

Моделирование коллекторов и, соответственно, классификация их параметров проводится по трём направлениям: геометрическое, механическое и связанное с наличием жидкости.

Геометрические модели.С геометрической точки зрения, все коллектора можно подразделить на две большие группы: гранулярные (поровые) (рис. 1.) и трещинные (рис.2). Ёмкость и фильтрация в пористом коллекторе определяется структурой порового пространства между зёрнами породы. Для второй группы характерно наличие развитой системы трещин, густота которых зависит от состава пород, степени уплотнения, мощности, структурных условий и так далее.

Чаще всего имеют место коллектора смешанного типа, для которых ёмкостью служат трещины, каверны, поровые пространства, а ведущая роль в фильтрации флюидов принадлежит развитой системе микротрещин, сообщающих эти пустоты между собой. В зависимости от вида путей фильтрации или главных вместилищ флюида различают коллектора: трещинно-пористые, трещинно-каверновые и т.д. При этом первая часть в названии определяет вид пустот, по которым происходит фильтрация.

Рис. 1.3. Слепок поровых

каналов сцементированного песчаника

Идеализированные модели пористых сред.Реальные горные породы имеют очень сложную геометрию (рис.1.3) порового пространства или трещин. Кроме того, размеры частиц гранулярных коллекторов или трещин в трещиноватых породах меняются в очень широких пределах – от микрометров до сантиметров. Естественно, что математическое описание течения через столь хаотическую структуру невозможно и, следовательно, необходима некоторая идеализация структуры.

Рис. 1.4. Элемент фиктивного грунта

С целью более точного описания реальных пористых сред в настоящее время предложены более сложные модели фиктивного грунта: с различными диаметрами шаров, элементами не шарообразной формы и так далее.

Идеальный грунт – среда, состоящая из трубочек одного размера, уложенных одинаковым образом по элементам из четырех трубочек в углах ромба. Плотность укладки меняется от угла раствора ромба.

Идеализированные модели трещинно-пористых сред. Трещинно-пористые коллекторы рассматриваются как совокупность двух разномасштабных пористых сред (рис.1.2): системы трещин (среда 1), где пористые блоки играют роль “зёрен”, а трещины – роль извилистых “пор” и системы пористых блоков (среда 2).

В простейшем случае трещинный пласт моделируется одной сеткой горизонтальных трещин некоторой протяженности (рис.1.5), причём все трещины одинаково раскрыты и равно отстоят друг от друга (одномерный случай).

Рис.1.5. Схема одномерной Рис.1.6 Схема пространственной

модели трещинной среды модели трещинной среды

В большинстве случаев трещинный пласт характеризуется наличием двух взаимно-перпендикулярных систем вертикальных трещин (плоский случай). Такая порода может быть представлена в виде модели коллектора, расчленённого двумя взаимно-перпендикулярными системами трещин с равными величинами раскрытия dи линейного размера блока породы l. В пространственном случае используют систему трёх взаимно-перпендикулярных систем трещин (рис.1.6).

Механические модели. Реологические модели горных пород. Всякое изменение сил, действующих на горные породы, вызывает их деформацию, а также изменение внутренних усилий – напряжений. Таким образом, динамическое состояние горных пород, как и флюидов, описывается реологическими соотношениями. Обычно реологические зависимости получают в результате анализа экспериментальных данных, натурных исследований или физического моделирования. Если объём пустот не изменяется или изменяется так, что его изменением можно пренебречь, то такую среду можно назвать недеформируемой. Если происходит линейное изменение объёма от напряжения, то такая среда – упругая, иначе ещё её называют кулоновской. К таким средам относятся песчаники, известняки, базальты. В упругих телах при снятии нагрузки объём восстанавливается полностью и линия нагрузки совпадает с линией разгрузки. Многие породы деформируются с остаточным изменением объёма, т.е. линия нагрузки не совпадает с линией разгрузки. Такие породы называются пластичными (глины), текучими (несцементируемые пески) или разрушаемыми.

Модели по ориентированности в пространстве. Горные породы необходимо разделять по ориентированности изменения их характеристик в пространстве. С этой позиции выделяют изотропные и анизотропные тела. Изотропия – это независимость изменения физических параметров от направления, анизотропия – различные изменения по отдельным направлениям. Понятие ориентированности, применительно к коллекторам, связано с геометрией расположения частиц, трещин. Частицы горной породы могут располагаться хаотически и упорядочно (иметь геометрическую ориентацию). Упорядочные структуры – анизотропны по поверхностным параметрам.

Характеристики коллекторов

С точки зрения теории фильтрации значение твердого скелета горной породы, прежде всего, геометрическое – он ограничивает ту область пространства, в которой движется жидкость. Свойства горных пород описываются некоторым набором геометрических характеристик, осредненных по достаточно малому, по сравнению с исследуемым объемом, но содержащему большое число элементов (частиц, пор, трещин).

Параметры пористой среды.Важнейшая характеристика – полная пористость «m_о«, равная отношению объема пор V_пк общему объему элемента V

.(1.1)

В связи с тем, что переток жидкости осуществляется через поверхность, представляется необходимым введение параметра, связанного с площадью. Такой геометрический параметр называется просветностью «m_s» и определяется как отношение площади просветов F_п ко всей площади сечения образца F

. (1.2)

Пользоваться такими поверхностными параметрами практически не представляется возможным, так как в реальных породах они меняются от сечения к сечению и определить их можно только с помощью микроскопического анализа. Следовательно, данные параметры следует заменить объемными, которые можно определить достаточно надежно. Выше отмечалось, что породы можно разделить на два класса: изотропные и анизотропные. Для анизотропных коллекторов с упорядоченной структурой данные параметры нельзя заменять на объемные. Для хаотичных, изотропных сред указанная замена возможна и просветность полагают равной пористости.

В реальных условиях твердые зерна породы обволакиваются тонкой плёнкой, остающейся неподвижной даже при значительных градиентах давления. В этом случае подвижный флюид занимает объём, меньший V_пo,и, поэтому, наряду с открытой пористостью часто пользуются понятием динамической (эффективной) пористости

,(1.3)

где V_под – объем, занятый подвижной жидкостью.

В дальнейшем, под пористостью мы будем понимать динамическую пористость, кроме специально оговорённых случаев.

Пористость твердых материалов (песок, бокситы и т.д.) меняется незначительно при изменении даже больших давлений, но пористость, например глины, очень восприимчива к сжатию. Так пористость глинистого сланца при обычном давлении равна 0.4 – 0.5, а на глубине 1800м – 0.05. Для газовых и нефтяных коллекторов в большинстве случаев m=15–22%, но может меняться в широких пределах: от нескольких долей процента до 52%.

Пористость и просветность фиктивного грунта не зависят от диаметра шарообразных частиц, а зависят только от степени укладки. Для реальных сред коэффициент пористости зависит от плотности укладки частиц и их размера – чем меньше размер зёрен, тем больше пористость. Это связано с ростом образования сводовых структур при уменьшении размера частиц.

В идеализированном представлении коэффициент пористости одинаков для геометрически подобных сред; он не характеризует размеры пор и структуру порового пространства. Поэтому для того, чтобы формулы, описывающие фиктивный грунт, можно было применить для описания реальной среды, вводится линейный размер порового пространства, а именно, некоторый средний размер порового канала d или отдельного зерна пористого скелета d.

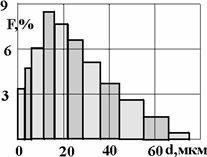
Рис.1.7. Гистограмма распределения частиц по размерам

Простейшая геометрическая характеристика пористой среды – эффективный диаметр частиц грунта. Определяют его различными способами – микроскопическим, ситовым, осаждением в жидкости (седиментационным) и так далее. Эффективным диаметром частиц d_э, слагающих реальную пористую среду, называют такой диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлическое сопротивление, оказываемое фильтрующейся жидкости в реальном и эквивалентном грунте, одинаково. Эффективный диаметр определяют по гранулометрическому составу (рис.1.7), например, по формуле веса средней частицы

, (1.4)

Для того, чтобы привести в соответствие диаметр частиц, определённый ситовым или микроскопическим методами, с гидравлическим, данный диаметр умножают на коэффициент гидравлической формы. Если же диаметры определяются гидродинамическими (седиментационными) методами, то они не требуют указанного уточнения.

Эффективный диаметр является важной, но не исчерпывающей характеристикой пористой среды, потому что он не даёт представления об укладке частиц, их форме. В то же время два образца грунта, имеющих равные эффективные диаметры, но различную форму частиц и структуру укладки, имеют различные фильтрационные характеристики.

Таким образом, для определения геометрической структуры пористой среды, кроме пористости и эффективного диаметра, нужны дополнительные характеристики. Одной из таких характеристик является гидравлический радиус пор R,который связанс диаметром частиц породы.

Динамика фильтрационного течения, в основном, определяется трением флюида о скелет коллектора, зависящего от площади поверхности частиц грунта. В связи с этим, одним из важнейших параметров является удельная поверхность S_уд – суммарная площадь поверхности частиц, содержащихся в единице объёма.

Удельная поверхность нефтесодержащих пород с достаточной точностью определяется формулой

, (1.5)

В практике нефтегазодобычи помимо чисто геометрической характеристики доли пустот (пористости) вводят параметры, связанные с наличием нефти, газа или воды:

а) насыщенность – отношение объёма V_fданного флюида, содержащегося в порах, к объёму пор V_п.

.(1.6)

По виду флюида различают нефтенасыщенность, газонасыщенность, водонасыщенность.

б) связанность – отношение объёма, связанного с породой флюида V_fс, к объёму пор

.(1.7)

Важнейшей характеристикой фильтрационных свойств породы является проницаемость. Проницаемость – параметр породы, характеризующий её способность пропускать флюиды. Различают проницаемости: абсолютную, эффективную или фазовую и относительную. Абсолютная проницаемость – свойство породы и не зависит от свойств фильтрующегося флюида и перепада давления, если нет взаимодействия флюидов с породой. Фазовойназывается проницаемость пород для данного флюида при наличии в порах многофазных систем. Значение её зависит не только от физических свойств пород, но также от степени насыщенности порового пространства флюидами и их физических свойств. Относительной проницаемостью называется отношение фазовой проницаемости к абсолютной.

Физический смысл проницаемости k заключается в том, что проницаемость характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация.

Для реальных сред радиус пор связан с проницаемостью формулой Котяхова

, (1.8)

где k – д; R – м;j – структурный коэффициент (j=0.5035/m 1,1 – для зернистых сред).

Проницаемость песчаных коллекторов обычно находится в пределах 100–1000 мд, а для глин характерны значения проницаемости в тысячные доли мдарси. Проницаемость определяется геометрической структурой пористой среды, то есть, размерами и формой частиц, а также системой их упаковки.

Имеется множество попыток теоретически установить зависимость проницаемости от этих характеристик, исходя из закона Пуазейля для ламинарного движения в трубах и Стокса для обтекания частиц при той или иной схематизированной модели пористой среды. Поскольку реальные породы не укладываются в рамки этих геометрических моделей, то теоретические расчеты проницаемости ненадёжны. Поэтому обычно проницаемость определяют опытным путём.

Проницаемость можно рассчитать по известной удельной поверхности:

. (1.9)

Параметры трещинной среды.Аналогомпористости для трещинных сред является трещиноватость m_т или, иначе, коэффициент трещиноватости. Иногда данный параметр называют трещинной пористостью. Трещиноватостью называют отношение объёма трещин V_т ко всему объёму Vтрещинной среды.

. (1.10)

Для трещинно-пористой среды вводят суммарную (общую) пористость, прибавляя к трещиноватости пористость блоков.

Второй важный параметр – густота. Густота трещин Г_т– это отношение полной длиныål_i всех трещин, находящихся в данном сечении трещинной породы к удвоенной площади сечения F

(1.11)

Из (1.11) следует, что для идеализированной трещинной среды

где d_т – раскрытость трещин; a – безразмерный коэффициент, равный 1,2, 3 для одномерного, плоского и пространственного случаев, соответственно.

Для реальных пород значение коэффициента a зависит от геометрии систем трещин в породе.

Для квадратной сетки трещин (плоский случай) Г_т=1 / l_т, гдеl_т – размер блока породы. Средняя длина трещин l* равняется среднему размеру блока породы и численно обратно пропорциональна густоте

В качестве раскрытости (ширины трещины) берут среднюю величину по количеству трещин в сечении F. Среднюю гидравлическую ширину определяют, исходя из гидравлического параметра – проводимости системы трещин.

Трещинный пласт – деформируемая среда. В первом приближении можно считать

, (1.14)

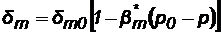
где d_т0 – ширина трещины при начальном давлении р₀ ;

b*_т=b_п l /d_т0– сжимаемость трещины; b_п – сжимаемость материалов блоков;l – среднее расстояние между трещинами.

Для трещинных сред l/d_т >100 и поэтому сжимаемость трещин высока.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

.1) На чем базируются построения математических и физических моделей?

2) Основные требования адекватности моделей реальным процессам.

3) Основное требование осреднения параметров по пространству, дающее право считать их непрерывным.

4) Почему в нефтяной гидромеханике процесс фильтрации флюидов можно считать изотермическим?

5) Назовите примеры нестационарных и стационарных процессов в нефтегазовой гидродинамике.

6) Модели флюидов по степени сжимаемости.

7) В чем отличие многофазной модели от гомогенной? Приведите примеры.

8) Определение ньютоновской и неньютоновских жидкостей. Примеры.

9) Виды моделей коллекторов с геометрической точки зрения.

10) Идеализированные модели пористых коллекторов.

11) Трещинно-пористые коллектора и их идеализация.

12) Реологические модели горных пород.

13) Какие среды называются изотропными и анизотропными?

14) Виды пористости и их определения? Размерности.

15) Виды проницаемости и их определения? Размерности в различных системах единиц и их связь между собой.

16) Что такое просветность?

17) Физический смысл проницаемости.

18) Определение эффективного диаметра.

19) Что такое насыщенность и связанность? Чему равна сумма насыщенностей? Размерности.

20) Удельная поверхность – определение, размерность, характерные значения для коллекторов.

21) Определение густоты.

22) Связь раскрытости с давлением.

23) Какой параметр определяется в Па*с?

24) Какой параметр определяется в дарси?

Скорость фильтрации

При исследовании фильтрационных течений удобно отвлечься от размеров пор и их формы, допустив, что флюид движется сплошной средой, заполняя весь объём пористой среды, включая пространство, занятое скелетом породы.

Предположим, что через поверхность F пористой среды протекает объёмный расход флюида

где `w – действительная средняя скорость жидкости; F_п – площадь пор.

Площадь пор связана с полной поверхностью через просветность (соотношение 1.2), а для сред неупорядочной структуры справедливо допущение о равенстве просветности и пористости. Следовательно,

называется скоростью фильтрации и определяет переток флюида, осреднённый по площади. Так какm u_кр соизмеримы с силами трения.

При обработке экспериментальных данных для определения критической скорости пользуются безразмерным параметром Дарси

, (2.16)

представляющим собой отношение сил вязкого трения к силе давления. В области действия закона Дарси данный параметр равен 1 и уменьшается при превышении числа Re критического значения.

. (2.17)

Законы фильтрации при Re > Re_кр. От точности используемого закона фильтрации зависит достоверность данных исследования скважин и определение параметров пласта. В связи с этим, в области нарушения действия закона Дарси необходимо введение нелинейных законов фильтрации. Данные законы могут быть: одночленными и двухчленными.

Одночленные законы описываются степенной зависимостью вида

(2.18)

где C, n – постоянные, 1£ n £ 2.

Данные зависимости неудобны, так как параметр n в общем случае зависит от скорости фильтрации. В связи с этим, наибольшее употребление нашли двучленные зависимости, дающие плавный переход от закона Дарси к квадратичному закону Краснопольского:

(2.19)

Коэффициенты А и В определяются либо экспериментально, либо теоретически. В последнем случае

(2.20)

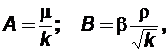
где b– структурный коэффициент и по Минскому определяется выражением

(2.21)

Трещинная среда

Линейный закон фильтрации.В трещинных пластах скорость фильтрации связана со средней скоростью через трещиноватость

Средняя скорость выражается через градиент давления по формуле Буссинеска при представлении течения по трещинам, как течения между двумя плоскими параллельными пластинами

(2.23)

Если использовать зависимости (2.23), (1.12), то получаем линейный закон фильтрации в трещинных средах

(2.24)

Проницаемость трещинных сред равна

(2.25)

Для трещинно-пористой среды общая проницаемость определяется как сумма пористой и трещинной проницаемостей.

Трещинно-пористую среду следует считать деформируемой. При таком подходе проницаемость трещинного пласта будет изменяться с изменением давления, а именно:

(2.26)

Данная зависимость справедлива при небольших изменениях давления. В общем случае необходимо использовать экспоненциальную связь деформации трещин с давлением.

Границы применимости линейного закона фильтрации.Так же, как и в пористых средах, в трещинных породах линейный закон может нарушаться при больших скоростях фильтрации из-за появления значительных по величине сил инерции. При этом значения критических чисел Рейнольдса значительно зависят от шероховатости: для гладких трещин Re_кр=500, а для шероховатых трещин – 0,4. Следует заметить, что если величина относительной шероховатости меньше 0.065, то её ролью в процессе фильтрации можно пренебречь.

Для трещинной среды выражение для числа Рейнольдса получается аналитически и равно

, а Re_кр=0,4. (2.27)

Начальные условия

если при t = 0 пласт не возмущён, тоj = j_о = const.

Граничные условия

Число граничных условий равно порядку дифференциального уравнения по координатам. Граничные условия задаются на границах пласта (внешние) и на забое скважины (внутренние).

А) Внешняя граница Г

т.е. граница является контуром питания;

2) постоянный переток массы через границу

G = Fr`u = const, т.е. используя уравнение (2.30),

(2.40)

3) переменный поток массы через границу

(2.41)

4) замкнутая внешняя граница

(2.42)

5) бесконечный пласт

В) Внутренняя граница

1) постоянный потенциал на забое скважины, радиуса r_c

2) постоянный массовый дебит (при условии выполнения закона Дарси) или

при r=r_c; (2.45)

3) переменный потенциал на забое

4) переменный массовый дебит

при r=r_c; (2.47)

5) неработающая скважина

при r=r_c. (2.48)

Замыкающие соотношения

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник