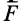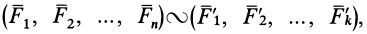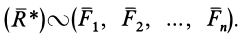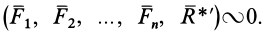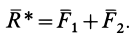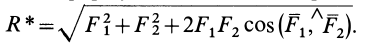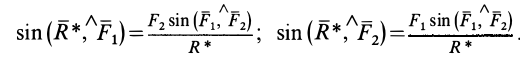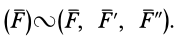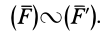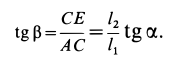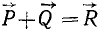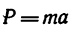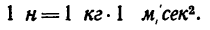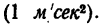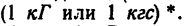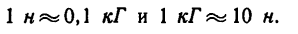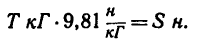На чем базируются все теоремы и уравнения статики
На чем базируются все теоремы и уравнения статики
Теоретическая механика – это наука о механическом движении твердых материальных тел и их взаимодействии. Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.
Статика изучает условия равновесия тел под действием сил.
Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.
Динамика изучает движение тел под действием сил.
Сила – это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т. е. сила – это величина векторная, характеризующаяся точкой приложения, направлением (линией действия), величиной (модулем).
Силы, действующие на тело (или систему сил), делят на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Системой сил называют совокупность сил, действующих на тело.
Эквивалентная система сил – система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами.
Первая аксиома. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
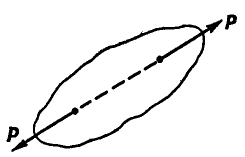
Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются.
Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешивающую систему сил (принцип отбрасывания системы сил, эквивалентной нулю).
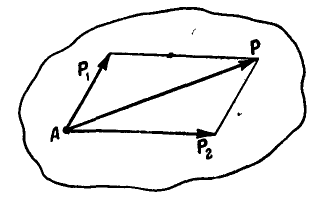
Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.
Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.
Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия.
2. Связи и реакции связей
Все тела делятся на свободные и связанные.
Свободные тела – это тела, перемещение которых не ограничено.
Связанные тела – это тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Связи делятся на несколько типов.
Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.
Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может.
Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry).
Защемление, или «заделка». Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Мz, препятствующий повороту.
Реактивная сила представляется в виде двух составляющих вдоль осей координат:
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n – число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
4. Определение равнодействующей аналитическим способом
Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Проекция силы на две взаимно перпендикулярные оси.
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.
Модуль (величину) равнодействующей можно определить по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской системы сходящихся сил:
При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
5. Пара сил. Момент силы
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.
Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом. Силы, входящие в пару, не уравновешиваются, так как они приложены к двум точкам.
Действие этих сил на тело не может быть заменено одной равнодействующей силой.
Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил плеча пары.
Тема 1.1. Основные понятия и аксиомы статики
§1. Элементы векторной алгебры
В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.
1. Понятие вектора.
Операции над векторами. Вектора можно складывать и умножать на число.
— сумма двух векторов есть вектор
— существует нулевой вектор
Рис.1. Сложение векторов
В математике все вектора являются свободными, их можно переносить параллельно самим себе.
В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.
Операции над векторами подчиняются следующим законам (см. рис.2):
Рис.2. Операции над векторами
2. Проекцией вектора на ось
Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис.3).
Рис.3. Проекция вектора на ось
§2. Основные понятия статики
Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.
Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не деформируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.
Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.
1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.
В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Сила является величиной векторной.
Ее действие на тело определяется:
1) численной величиной или модулем силы
2) направлением силы
3) точкой приложения силы (рис.4).
Рис.4. Сила, приложенная к телу
Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.
Прямая DE, вдоль которой направлена сила, называется линией действия силы.
Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.
2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. Предполагается, что действие силы на тело не изменится, если ее перенести по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.
3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.
4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.
Например, если системы сил, изображенных на рис. 5, а и рис. 5, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.
Рис 5. Система сил:
а – заданная система сил; б – эквивалентная система сил
5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю.
7. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.
8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.
9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной.
Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.
Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, представляют собою по существу равнодействующие некоторых систем распределенных сил.
В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равнодействующую сил тяжести его частиц. Линия действия этой равнодействующей проходит через точку, называемую центром тяжести тела.
§3. Аксиомы статики
Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны (рис. 6).
Рис.6. Система сил, находящаяся в равновесии
Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.
Аксиома 2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.
Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.
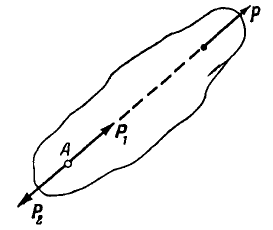
Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
Рис.7. Система сил
В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.7). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы
Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.
Рис.8. Равнодействующая двух сил
Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.
(рис. 9). Однако силы и не образуют уравновешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.
Рис.9. Противодействие
Рис. 10. Опирание балки на опоры:
а – схема загружения балки; б – силы действия балки на
опоры и противодействия со стороны опор на балку
Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.
Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.
Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).
Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.
Видео-урок «Аксиомы статики»
§4. Связи и их реакции
По определению, тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.
Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.
Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так:
Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.
Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.
Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равновесии, заменим стол силой, направленной вверх и равной, конечно, весу тела.
Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.
Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.
Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.
Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.
Рассмотрим, как направлены реакции некоторых основных видов связей:
1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.11, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 11, б), то реакция направлена по нормали к другой поверхности.
Аксиомы и теоремы статики в теоретической механике
Содержание:
В статике твердого тела рассматриваются свойства сил, приложенных к твердому телу. В частности, изучается приведение сложных систем сил к более простому виду и устанавливаются условия равновесия различных систем сил, действующих на твердое тело или материальную точку.
Теоретическая механика, как и всякая другая наука, имеет свои понятия и определения, которые используются для формулирования ее аксиом и теорем. Статика базируется на аксиомах, из которых по законам логики, вводя новые понятия, получают все необходимые следствия в удобной для применения форме.
Основные понятия и определения аксиом
Материальной точкой называют простейшую модель материального тела любой формы, размеры которого достаточно малы и которое можно принять за геометрическую точку, имеющую определенную массу.
Механической системой называется любая совокупность материальных точек.
Абсолютно твердым телом (или неизменяемой механической системой) называют механическую систему, расстояния между точками которой не изменяются при любых взаимодействиях. Все тела в природе в той или иной мере деформируемы, но в некоторых задачах деформациями тел можно пренебречь, считая тела твердыми. При рассмотрении движения Земли вокруг Солнца ее можно считать абсолютно твердым телом и даже материальной точкой, хотя в действительности она не твердая, так как на ней есть океаны, воздушная оболочка и т. д. В дальнейшем абсолютно твердое тело будем называть просто твердым телом.
Понятие силы в теоретической механике является основным, первичным понятием. Силой называют одну из векторных мер действия одного материального объекта на другой рассматриваемый объект. Имеются разные меры действия: скалярные и векторные. Обычно за эталон числового значения силы принимают значение линейной силы упругости, например пружинного динамометра, которая пропорциональна его деформации. Числовые значения сил различной природы определяют путем сравнения со значением линейной силы упругости.
Сила кроме числового значения характеризуется точкой приложения и направлением действия. Она является векторной величиной. Механическое действие материальных тел друг на друга осуществляется при их соприкосновении (давление стула на пол в местах соприкосновения его ножек с полом) или как действие на расстоянии при посредстве силовых полей (притяжение Луны Землей и т. п.).
Силу как величину векторную обозначают какой-либо буквой со знаком вектора, например
Системой сил называют совокупность сил, действующих на рассматриваемое тело или в более общем случае на точки механической системы. Можно рассматривать систему сил, приложенных к одной материальной точке.
Системой сил, эквивалентной нулю (или равновесной системой сил), называют такую систему сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.
Две системы сил называются эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях, т. е. если одна система сил приводит твердое тело или материальную точку в какое-то движение, например из состояния покоя, то другая система сил, эквивалентная первой, сообщит такое же движение. Движения, вызванные действием эквивалентных систем сил, имеют одинаковые характеристики для каждого момента времени. Условие эквивалентности двух систем сил 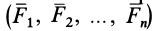
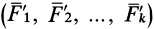
где 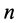
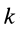
Равнодействующей силой рассматриваемой системы сил называют силу, действие которой на твердое тело или материальную точку эквивалентно действию этой системы сил. Равнодействующая сила обозначается 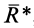
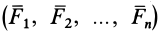
Равновесная система сил имеет равнодействующую, равную нулю.
Уравновешивающей силой заданной системы сил считается такая сила, добавление которой к заданной дает новую систему, эквивалентную нулю. Если 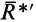
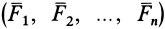
В дальнейшем убедимся, что не всякая система сил имеет равнодействующую и уравновешивающую силы. Есть системы сил, которые не находятся в равновесии и не эквивалентны одной силе.
Аксиомы статики
Справедливость аксиом механики проверяется на опыте как непосредственно, так и по тем следствиям, которые из них получают.
При формулировке аксиом предполагаем, что на твердое тело или материальную точку действуют силы, которые указаны в соответствующей аксиоме. Твердое тело или материальную точку в общем случае следует считать свободными, имеющими возможность совершать в рассматриваемый момент любые перемещения в пространстве.
Аксиома о равновесии системы двух сил
Для равновесия системы двух сил, приложенных к точкам твердого тела, необходимо и достаточно, чтобы эти силы были равны по модулю и действовали вдоль одной прямой, проходящей через точки их приложения, в противоположных направлениях (рис. 1). Этой аксиомой устанавливается простейшая система сил, эквивалентная нулю. Если силы 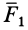
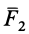
Аксиома о добавлении (отбрасывании) системы сил, эквивалентной нулю
Если на твердое тело действует система сил, то к ней можно добавить (отбросить) систему сил, эквивалентную нулю. Полученная после добавления (отбрасывания) новая система сил является эквивалентной первоначальной системе сил. Под действием заданной системы сил и новой, полученной после добавления (отбрасывания) равновесной системы сил, тело будет двигаться (или находиться в покое) совершенно одинаково при прочих равных условиях. В частности, к любой системе сил можно добавить (отбросить) простейшую равновесную систему сил, состоящую из двух равных по модулю сил, действующих вдоль одной прямой в противоположных направлениях и приложенных в одной или разных точках твердого тела в соответствии с первой аксиомой.
Рис. 1
Аксиома параллелограмма сил
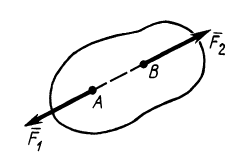
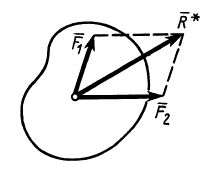
Две силы, действующие в одной точке твердого тела или на одну материальную точку, можно заменить одной равнодействующей силой, равной по модулю и направлению диагонали параллелограмма, построенного на заданных силах (рис. 2). Очевидно, справедливо и обратное. Одну силу, приняв за равнодействующую, можно разложить по правилу параллелограмма на две составляющие силы.
Рис. 2
Эту аксиому долгое время в истории развития механики пытались доказать и, следовательно, считали теоремой. Тщательный анализ таких доказательств, часто очень остроумных, показал, что для этого дополнительно используются положения, которые следует принимать за аксиомы.
Замену двух сил одной равнодействующей силой по правилу параллелограмма называют векторным сложением этих сил. Векторное сложение сил 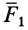
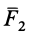
Если силы 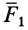
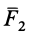
Модуль равнодействующей силы 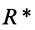
Применяя теорему синусов к одному из треугольников параллелограмма, определяют синусы углов, которые образует равнодействующая r* с составляющими ее силами 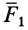
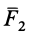
Более предпочтительным способом определения числового значения и направления равнодействующей силы по отношению к каким-либо прямоугольным осям координат является метод проекций, который особенно удобен в случае векторного сложения более чем двух сил. Этот метод рассматривается дальше, при изучении систем сходящихся сил.
Аксиома о равенстве сил действия и противодействия
Аксиома о равенстве сил действия и противодействия — один из основных законов классической механики, сформулированных Ньютоном: всякой силе действия есть равная, но противоположная сила противодействия. По отношению к двум материальным точкам эта аксиома утверждает, что силы взаимодействия двух материальных точек равны по модулю, противоположны по направлению и действуют вдоль одной прямой, проходящей через взаимодействующие точки. Материальные точки при этом могут взаимодействовать как через посредство силовых полей, т. е. на расстоянии, так и путем соприкосновения друг с другом, если их считать твердыми телами очень малых размеров.
В статике эту аксиому применяют для твердых тел. Силы взаимодействия двух твердых тел (при взаимодействии путем соприкосновения или на расстоянии при посредстве силовых полей) равны по модулю и противоположны по направлению. Силы действия и противодействия всегда приложены к разным телам или к различным взаимодействующим точкам одного и того же тела.
Таким образом, в природе силы встречаются всегда по две: силы действия и противодействия.
Аксиома связей
Связью для твердого тела или материальной точки называют материальные объекты (тела и точки), которые ограничивают свободу перемещения рассматриваемого твердого тела или материальной точки. Аксиома связей утверждает, что всякую связь можно отбросить и заменить силой, реакцией связей (в простейшем случае) или системой сил (в общем случае). Эта аксиома фактически уже содержится в определении силы, но в истории развития механики это не было осознано сразу. Длительное время после формулировки Ньютона основных законов классической механики их применение к несвободным твердым телам и механическим системам встречалось с трудностями, пока не была дополнительно сформулирована аксиома связей. Учитывая большое значение аксиомы связей для дальнейшего изложения теоретической механики, оставим эту аксиому как самостоятельную.
Почти все теоремы и окончательные результаты теоретической механики формулируются для материальной точки или твердого тела, освобожденных от связей, т. е. когда связи заменены силами реакций связей. Поэтому очень важно уметь правильно заменять отброшенные связи силами реакций связей. Это одна из главных задач при изучении статики, которой следует уделить наибольшее внимание.
Силы реакций связей для рассматриваемого тела или точки зависят прежде всего от приложенных сил и от вида связей. При движении силы реакций связей зависят еще и от характеристик движения. Так, при движении тела в воздухе сила реакции воздуха на движущееся тело зависит от скорости движения тела относительно воздуха.
Рис. 3
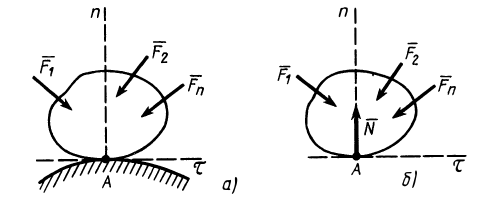
Приведем примеры связей и их замены силами реакций связей. Если связью для твердого тела (рис. 3, а) является абсолютно гладкая поверхность другого тела, то сила реакции такой поверхности, если соприкосновение происходит в одной точке, направлена по нормали к общей касательной соприкасающихся поверхностей тел независимо от сил, приложенных к рассматриваемому телу (рис. 3, б). Сила реакции связи 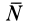
Если соприкосновение происходит не в одной точке, а по некоторой площади поверхности, то реакция такой связи сводится к системе распределенных по поверхности сил, которые в некоторых случаях удается заменить одной равнодействующей силой реакции связи. В общем случае система распределенных сил может не иметь равнодействующей.
В тех случаях, когда сила реакции связей не только по модулю, но и по направлению зависит от приложенных сил, ее обычно раскладывают по правилу параллелограмма на составляющие параллельно осям координат. Через составляющие легко определяется как модуль силы реакции, так и ее направление.
Рис. 4
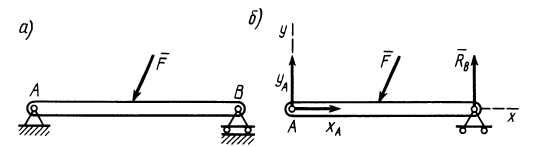
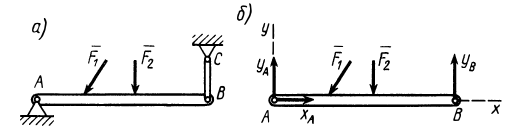
Неизвестную по модулю и направлению силу реакции создают цилиндрический (плоский) и шаровой шарниры. Пусть имеем балку 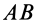
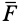
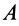
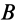
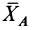
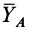
В случае шарового шарнира силу реакции раскладывают на три составляющие, параллельные осям координат.
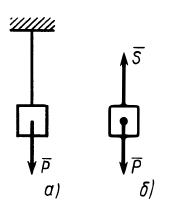
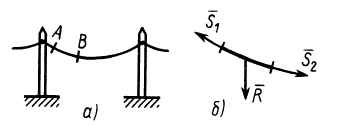
Гибкие связи (канаты, тросы, нити) дают силы реакции связей (силы натяжения), направленные по касательной к гибкой связи. На рис. 5, а, б сила натяжения нити заменяет действие нити на груз. На рис. 6, а, б показаны силы натяжения провода в сечениях 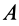
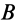
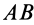
Рис. 5
Рис. 6
Рис. 7
Силы реакций других наиболее часто встречающихся связей рассматриваются в примерах.
Аксиома затвердевания
Если деформируемое тело находится в равновесии, то равновесие его без изменения системы приложенных сил не нарушится от наложения на точки тела дополнительных связей, включая превращение деформируемого тела в абсолютно твердое. С помощью этой аксиомы устанавливается, в частности, связь между условиями равновесия сил, приложенных к твердому и деформируемому телам. Из аксиомы следует, что условия равновесия сил, приложенных к твердому телу, необходимы и для равновесия деформируемого тела. Но условия равновесия сил, приложенных к твердому телу, не являются достаточными для равновесия деформируемого тела.
Сформулированные аксиомы и являются той основой, на которой строится вся статика сил, приложенных к твердому телу.
Аксиомы статики характеризуют свойства сил, приложенных к абсолютно твердому телу или одной точке. Но они не учитывают материальных свойств тела или точки, характеризуемых их массой, а для тела — еще распределением массы в теле, влияние которых существенно при их движении.
Совместный учет действия сил и материальных свойств тел или точки содержится в аксиомах динамики. Такие аксиомы статики, как аксиома о параллелограмме сил, о равенстве сил действия и противодействия, аксиома связей, справедливы и в динамике. Так как в статике рассматриваются свойства и неравновесных систем сил, под действием которых твердое тело или точка не могут находиться в покое относительно инерциальной системы отсчета, то для оправдания этого в статике можно считать, что эти системы сил являются частями более укрупненных равновесных систем сил, под действием которых тело или материальная точка находится в покое или совершает движение по инерции.
Простейшие теоремы статики
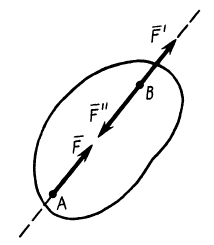
Теорема о переносе силы вдоль линии действия
Действие силы на твердое тело не изменится от переноса силы вдоль своей линии действия.
Пусть в точке 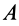
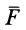
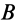
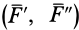
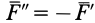
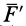
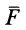
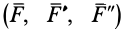
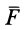
Система сил 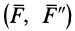
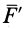
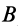
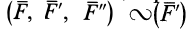
Сила 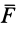
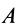
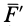
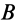
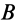
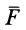
Рис. 8
Теорема о трех силах
Если твердое тело под действием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то линии действия таких трех сил пересекаются в одной точке.
Обратная теорема неверна, т. е. если линии действия трех сил пересекаются в одной точке, то такая система сил не обязательно является равновесной.
Пусть имеем систему трех сил 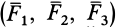
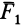
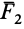
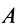
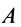
Силы 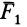
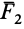
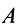
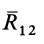
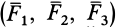
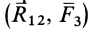
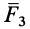
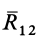
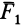
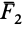
Теорема о трех силах позволяет в некоторых случаях определить линию действия неизвестной силы, приложенной к твердому телу.
Рис. 9
Рис. 10
Рис. 11
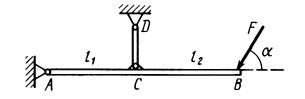
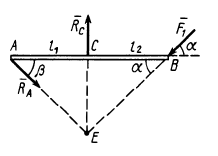
Пример. Дана балка 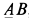
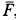
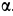
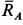
Решение. Освободим балку от связей, заменив их силами реакций связей (рис. 11). Сила реакции стержня 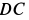
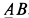
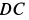
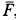
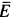
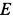
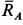
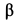
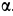
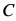
Если 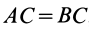
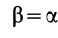
Всё о аксиомах статики
Как было указано выше, статика изучает условия относительного равновесия твердых тел или механических систем, находящихся под действием сил.
Силы возникают в результате взаимодействия между собой различных материальных тел. По своей природе сила является величиной векторной и вполне определяется, если известны ее точки приложения (или линия действия), направление и величина.
Величина силы измеряется при помощи прибора, называемого динамометром, и может быть выражена в единицах веса. За единицу силы мы в дальнейшем примем вес 1 л воды при 4°С; такая единица силы называется килограммом и обозначается сокращенно через кГ.
Линией действия силы называется прямая, вдоль которой направлена сила. В дальнейшем мы. будем обозначать силы жирными буквами Р, Q, F, N, а их численные значения (модули) светлыми буквами Р, Q, F, N... Несколько сил, приложенных к твердому телу, представляют систему сил.
Если твердое тело под действием системы сил остается в покое или движется по отношению к выбранным координатным осям так, что все его точки имеют одинаковые скорости и движутся прямолинейно и равномерно, то такое тело находится в состоянии равновесия, а силы, приложенные к нему, образуют уравновешивающуюся систему. Любая из сил уравновешивающейся системы является уравновешивающей по отношению к остальным силам.
Две системы сил называются эквивалентными, если при замене одной системы сил, приложенных к твердому телу, другой системой не нарушается покой тела, или если тело находилось в движении, то не изменяется это движение.
Если система сил эквивалентна одной силе, то эта сила называется равнодействующей системы, а отдельные силы системы по отношению к их равнодействующей называются составляющими силами.
В основу изучения статики положены истины, которые на протяжении многих столетий подтверждаются опытом. Эти истины, как было указано выше, называются аксиомами статики.
В дальнейшем, для краткости изложения, тело мы будем называть просто телом.
Аксиома 1. Две силы, приложенные к свободному телу, взаимно уравновешиваются тогда, и только тогда, когда они равны по величине и направлены по одной прямой в противоположные стороны.
Эта аксиома выражает, условие равновесия двух сил Р, приложенных к телу (рис. 17).
Аксиома 2. Присоединение и отбрасывание сил, взаимно уравновешивающихся, не изменяет действия сил, приложенных ранее к телу.
На основании этой аксиомы можно вывести важное следствие.
Пусть мы имеем силу Р, действующую на тело (рис. 18).
Возьмем на линии действия этой силы любую точку А и, согласно аксиоме 2, приложим в этой точке две силы 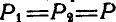
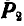
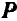
вместо силы Р получим силу 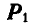
Отсюда следует, что не нарушая действия силы на тело, силу можно переносить в любую точку вдоль ее линии-действия. Следовательно, сила, приложенная к твердому телу, является вектором, скользящим или передвижным.
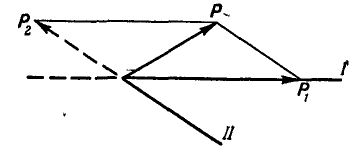
Аксиома 3. Равнодействующая двух сил, приложенных в одной точке и составляющих между собой некоторый угол, приложена в этой же точке и выражается по величине и направлению диагональю параллелограмма, построенного на данных силах.
Обозначим равнодействующую двух сил 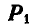
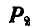
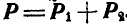
Последнее равенство обозначает операцию геометрического сложения сил 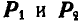
Обратно, всякую силу Р можно разложить на составляющие 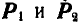
Эти линии отсекут на заданных направлениях I и II искомые составляющие силы 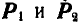
Аксиома 4. Силы, с которыми два тела действуют друг на друга, всегда равны по величине и направлены по одной прямой в противоположные стороны.
Эта аксиома выражает равенство действия и противодействия при взаимодействии друг на друга двух тел. Так, например известно, что между Землей и Луной имеются силы взаимного притяжения, причем эти силы равны по величине и направлены по прямой, соединяющей центры Земли и Луны, в противоположные стороны. Точно так же, если на неподвижной горизонтальной плоскости покоится шар, то действие шара на плоскость будет передаваться в точке касания плоскости и шара в виде давления, равного весу шара, направленного вертикально вниз.
В свою очередь, плоскость в той же точке будет действовать на шар вверх.
Эта сила называется реакцией плоскости; она равна по величине ддвлению и направлена вертикально вверх.
Аксиома 5. Равновесие нетвердого тела не нарушается, если это тело станет абсолютно твердым.
Эта аксиома, называемая принципом затвердения, находит широкое применение при изучении равновесия нетвердых тел.
Аксиома 6. Если тело несвободное, то действие связей на тело может быть заменено их реакциями.
При решении большинства задач механики приходится иметь дело с телами несвободными. Движение таких тел ограничено опорами или направляющими, которые являются связями для тел. В тех местах, где тело соприкасается со связями, происходят взаимодействия между телом и связями; эти взаимодействия могут быть представлены в виде сил. Силы, с которыми связи действуют на тело, называются реакциями связей, или просто реакциями, а равные и противоположно направленные им силы, представляющие действие тела на связи, называются давлениями.
На основании последней аксиомы при решении задач статики можно связи отбросить и рассматривать, например, равновесие несвободного тела, как тела свободного, находящегося под действием заданных сил и реакций связей. Такой прием удобен, как мы увидим дальше, при решении многих задач статики, где силами, подлежащими определению, являются реакции связей.
Различные виды связей и реакции, которыми эти связи могут быть заменены, рассмотрены в следующем параграфе.
Справочный материал о аксиомах статики
Статикой называют раздел механики, в котором изучают преобразования системы сил, приложенных к твердому телу, в системы, ей эквивалентные, и условия взаимной уравновешенности сил, приложенных к твердому телу
Предмет статики
Рассмотрим систему сил, приложенных к одному абсолютно твердому телу. Изучение возможности замены такой системы сил другими системами, оказывающими на данное тело такое же механическое воздействие, и, в частности, изучение условий взаимной уравновешенности сил, приложенных к твердому телу, составляют предмет статики.
Таким образом, статикой называют раздел механики твердого тела, в котором изучают преобразование системы сил, приложенных к твердому телу, в системы, ей эквивалентные, и условия взаимной уравновешенности таких систем.
В высших технических учебных заведениях курс теоретической механики обычно начинают со статики. Такое построение курса обусловлено требованиями учебных планов, необходимостью возможно раньше ознакомить студента со статикой как обязательной предпосылкой для курса сопротивления материалов и всех последующих инженерно-технических дисциплин. Имеет значение и то, что для изучения статики высшая математика не нужна в столь большом объеме, в котором она требуется для других разделов механики. Наконец, как уже было упомянуто, такое построение соответствует и историческому развитию нашей науки.
Исторические корни статики уходят в глубокую древность. Со времен Архимеда учение о силах и их равновесии является уже вполне сложившейся наукой. Крупными вехами в дальнейшем развитии статики явились открытие Стевином закона параллелограмма сил (см. § 3) и открытие современником Ньютона Вариньоном (1654—1722) его знаменитой теоремы о моменте равнодействующей силы (см. § 8). Однако окончательное оформление статика получила лишь после исследований Пуансо и, в частности, после открытия им метода приведения силы к данной точке (см. § 11).
Статика базируется на основных законах, принимаемых без математических доказательств и называемых аксиомами статики
Механика — наука точная
Все свои теоремы и правила она выводит путем строгих математических выкладок. Однако в основе механики и, в частности, статики лежат аксиомы—законы, принятые без математического доказательства. Математических доказательств этих законов не существует, хотя законы эти настолько просты, что кажутся очевидными. Под аксиомой механики мы не будем понимать какую-то непреложную и настолько очевидную истину, что даже доказательство ее совершенно излишне. Они представляют собой результат обобщения выводов, полученных из многолетних и многочисленных опытов и наблюдений над движением и покоем тел. Мы не имеем возможности проверить их непосредственно и располагаем лишь косвенными доказательствами, т. е. мы видим, что следствия, вытекающие из этих аксиом, подтверждаются наблюдениями: сооружения, построенные на основании законов механики, прочны, машины работают, приборы и аппараты действуют, корабли плавают, самолеты летают, запущенные нами космические корабли выходят на предписанные им орбиты, а затмения Солнца и Луны происходят в точности так, как это было заранее предсказано. Все это является доказательством правильности всех положений механики (в частности, ее аксиом), на основе которых были рассчитаны эти сооружения, сконструированы машины и произведены астрономические вычисления, потому что верные практические результаты могут быть получены только из правильных
предпосылок.
В статике принимают обычно шесть аксиом: принцип инерции, аксиому об абсолютно твердом теле, аксиому о присоединении уравновешенной системы сил, закон параллелограмма, принцип равенства действия и противодействия, аксиому о затвердении.
«Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние» (Ньютон)
Принцип инерции
Принцип (т. е. основоположение, с позиции которого надо рассматривать всякое механическое явление) инерции был сформулирован Ньютоном и принят им в качестве первого основного закона механики. Закон утверждает, что всякое тело должно находиться в состоянии покоя или равномерного прямолинейного движения, пока это состояние не будет изменено действующими на тело силами. Ньютон ничего не говорит о размерах тела, но в дальнейшем он показывает, что высказанные им аксиомы относятся к отдельной материальной частице или же к центру тяжести, в котором предполагается сосредоточенной масса всего тела. Таким образом, здесь под телом надо понимать материальную точку.
Проявление присущего материи свойства сохранять механическое движение, без действия сил сохранять свою скорость, называют инерцией.
Аксиома инерции содержит в себе как бы две части — аксиома инерции покоя и аксиома инерции движения. Та часть, которая утверждает, что тело остается в покое, пока силы не изменят этого состояния, очевидна и подтверждается повседневным опытом: мы никогда не видели, чтобы покоящиеся тела сами, без действия на них сил, приходили в движение. Эта так называемая инерция покоя была известна еще со времен Аристотеля.
Напротив, открытое Галилеем свойство материальных тел без действия сил сохранять состояние равномерного и прямолинейного движения (инерция движения) на первый взгляд как будто бы противоречит повседневному опыту. И движущиеся тела обычно нуждаются в постоянном действии силы для поддержания движения: чтобы передвигать телегу, нужна конская тяга, парусное судно без ветра не движется и т. д. Однако это противоречие закона инерции движения нашим повседневным наблюдениям только кажущееся. В обыденной жизни мы не встречаем тел, на которые не действовали бы никакие силы, на всяком движущемся теле всегда сказываются действия других тел. Катящаяся телега испытывает- сопротивление дороги, трение в осях, сопротивление воздуха; плывущее судно претерпевает сопротивление воды и воздуха. Эти силы (их называют диссипативными) и замедляют движение тел. Диссипативные силы невозможно уничтожить, но их иногда возможно значительно уменьшить.
Например, в машине можно смазать трущиеся части, заменить подшипники скольжения шариковыми подшипниками и т. п. Чем меньше диссипативные силы, тем дольше тело сохраняет свое движение. Велосипед, находящийся в хорошем состоянии, на свободном ходу катится дольше, чем старый и запущенный велосипед.
Отсюда можно заключить, что если бы нам удалось совершенно устранить сопротивление движению тела, то движение было бы равномерным. Вместе с тем, очевидно, движение было бы и прямолинейным, если, конечно, никакие силы не заставили бы это тело свернуть со своего прямолинейного пути. Практически невозможно никакой смазкой полностью уничтожить силы сопротивления. Поэтому для поддержания движения к телу необходимо приложить силу. Эта сила нужна не для осуществления движения, а лишь для преодоления сопротивлений. Для равномерного и прямолинейного движения нужна в точности такая движущая сила, какая необходима для преодоления сил сопротивления. Действительно, если движущая сила меньше сил сопротивления, то движение тела постепенно замедляется и тело останавливается. Если она больше сил сопротивления, то тело движется ускоренно. Если же движущая сила равна силе сопротивления, то не происходит ни замедления, ни ускорения—тело движется равномерно и, разумеется, прямолинейно.
Две силы, действующие на твердое тело, взаимно уравновешиваются тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны
Аксиома об абсолютно твердом теле. При равномерном движении или при покое тела движущая сила и сила сопротивления как бы уничтожают, или, как говорят, уравновешивают друг друга. Очевидно, что для равновесия двух сил, действующих на какое-либо твердое тело, точнее говоря, для того, чтобы твердое тело находилось в равновесии под действием только двух сил, необходимо, чтобы они были равны по величине, противоположны по направлению и действовали по одной и той же прямой. Если они направлены в противоположные стороны по одной и той же прямой, но не равны по величине, то тело приобретает ускоренное движение в сторону большей силы. Если же две силы, хотя бы и равные между собой, действуют по пересекающимся или скрещивающимся прямым, ю они тоже не могут уравновесить друг друга. Случай двух сил, направленных по разным прямым и приложенных к одной точке, рассмотрен в аксиоме параллелограмма. Такие две силы не находятся в равновесии. Две силы не уравновешивают друг друга и в том случае, если они действуют на одно и то же тело в противоположные стороны, но не по одной, а по параллельным прямым, что подробно рассмотрено в гл. IV.
Сформулируем условия равновесия двух сил: две силы, действующие на твердое тело, взаимно уравновешивают друг друга в том и только в том случае, если они равны по величине и действуют в противоположные стороны по одной и той же прямой. Это не только необходимые, но и достаточные условия равновесия двух сил.
Напомним, что здесь, как и всюду в теоретической механике, под твердым телом мы понимаем абсолютно твердое тело. Совершенно ясно, что две такие силы, приложенные к какому-либо реальному физическому телу, могут вызвать деформацию и даже разрушение тела. Лишь на абсолютно твердое тело такие взаимно уравновешенные силы никакого действия оказать не могут. Поэтому рассмотренную аксиому следует называть аксиомой об абсолютно твердом теле.
От присоединения к телу или отбрасывания от него уравновешенной системы сил равновесие тела не нарушается
Аксиома о присоединении уравновешенной системы сил. Взаимно уравновешенная система сил — это такая система, наличие которой эквивалентно ее отсутствию. В самом деле, поскольку согласно аксиоме об абсолютно твердом теле две взаимно уравновешенные силы не могут изменить движение или нарушить покой тела, мы вправе сделать
заключение, что такая взаимно уравновешенная система сил никак не влияет на твердое тело. Как мы скоро убедимся, взаимно уравновесить друг друга могут не только две силы, но и любое большее количество сил. Вообще под уравновешенной системой сил понимают совокупность сил, которая, будучи приложена к твердому телу, находящемуся в покое, не выводит его из этого состояния.
В статике принимают как аксиому, что равновесие твердого тела не нарушится, если к телу приложить или от него отбросить взаимно Уравновешенную систему сил. Если же твердое тело находилось не в покое, а в движении перед тем, как мы приложили к нему или отбросили от него взаимно уравновешенную систему сил, то движение тела от этого не изменится.
Всякая данная система сил, действующих на твердое тело, и другая система, полученная из данной путем присоединения или отбрасывания уравновешенной системы сил, оказывает на твердое тело, совершенно одинаковое действие. Обе эти системы эквивалентны.
Действие силы на твердое тело не изменится, если эту силу перенести по линии ее действия.
Сила как скользящий вектор
Докажем теорему, согласно которой всякую силу, действующую на абсолютно твердое тело, можно перенести по прямой, по которой эта сила направлена, в какую-либо другую точку тела, отчего действие силы не изменится.
Пусть на тело действует сила F, приложенная к телу в точке А (рис. 1, а). Прямую линию, вдоль которой направлен вектор силы, называют линией действия силы, или прямой действия силы. Возьмем наней произвольную точку В и приложим к телу в этой точке две силы F1 и F2, численно равные силе F и направленные по той же линии действия, причем пусть F1 направлена в ту же сторону, что и F, a F2 — в противоположную (рис. 1, б).
Действие силы F на тело не изменилось от приложения к нему взаимно уравновешенных сил F1 и F2. Но силы F и F2 также являются двумя равными и противоположно направленными силами, действующими на то же абсолютно твердое тело по одной и той же прямой. :Можно отбрасывать такие уравновешенные системы сил. Отбросив F и F2 (рис. 1, в), убедимся, что на тело действует только одна сила F1, которая представляет собой силу F, перенесенную вдоль линии действия в другую точку, что и требовалось доказать. Это свойство силы выражают словами: сила есть вектор скользящий. Выражение образное и очень распространенное, но не вполне правильное, так как оно характеризует свойство не вектора, а абсолютно твердого тела.
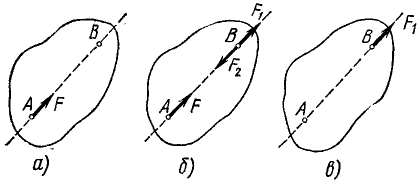
Рис. 1
Наши рассуждения символически можно записать так:
Каждая из сил F и F1 может быть уравновешена одной и той же силой F2. Силу F2, которая, будучи приложенной к твердому телу, уравновешивает данную силу F, называют уравновешивающей данную силу. Две силы F и F1 называют эквивалентными, т. е. равноценными по своему действию на тело, если они имеют одну и ту же уравновешивающую силу.
Это понятие распространяется и на систему сил: системы сил, имеющие одну и ту же уравновешивающую систему сил, называют эквивалентными системами сил.
Равнодействующая двух сил, приложенных к одной точке н направленных под углом друг к другу, изображается по величине и направлению диагональю параллелограмма, построенного на этих силах как на сторонах
Закон параллелограмма сил
Две силы, приложенные к одной материальной частице и направленные под углом друг к другу, эквивалентны одной силе, называемой равнодействующей силой; эта равнодействующая может быть представлена как диагональ параллелограмма, построенного на данных силах как на сторонах, частице О твердого тела приложены две силы: 1) по величине равная P и направленная по прямой OA и 2) по величине равная Q и направленная по прямой OB (рис. 2). Мы представим эти силы в виде векторов, т. е. изобразим силу P вектором 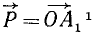
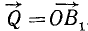
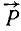
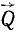
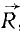
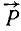
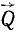
Это правило называют правилом параллелограмма, а самый процесс—сложением сил по способу параллелограмма. Название это нельзя признать удачным, так как физического сложения сил не происходит, равнодействующая не есть сумма слагаемых сил, а лишь равноценна им обеим, вместе взятым. Пусть, например, два трактора тянут какой-либо груз О: один с силой 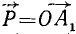
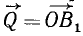
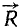
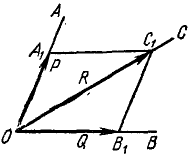
Рис. 2
Сложение сил, направленных под углом друг к другу, называемое геометрическим сложением, сильно отличается от сложения величин, к которому мы привыкли в арифметике и в алгебре.
Геометрическое сложение обозначается обычным знаком « + », но над слагаемыми и над суммой ставят стрелки, означающие, что это векторные величины.
Геометрические равенства выглядят иногда необычно с точки зрения арифметики.
Так, например, на рис. 3, а сила P = 3 н и сила Q = 4 н перпендикулярны друг другу; по теореме Пифагора находим R= 5 н; на рис. 3,б сила Р = 3 н и сила Q = 3 н по той же теореме 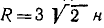
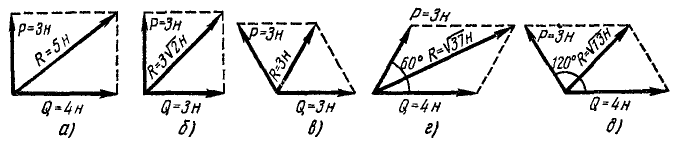
Рис. 3
те же, но направлены они под углом 120 о друг к другу, а потому R = 3 н; на рис. 3, г сила Р = 3 н, сила Q = 4 н и направлены они под углом 60° друг к другу. Применяя теорему косинусов, находим R 2 = 9 + 16—2∙3∙4∙cos 120° = 37 н; иа рис. 3, д те же силы составляют угол 120° и по той же теореме R 2 = 9+ 4-16—2∙3∙4∙cos60°=13 н.
Из геометрии известно, что диагональ параллелограмма всегда меньше арифметической суммы его непараллельных сторон и больше их разности. Поэтому, если в геометрической сумме
P больше Q, то всегда имеет место алгебраическое неравенство
P-Q≤R≤P+Q.
Равенство P+Q = R имеет место, если силы P и Q направлены по одной прямой и в одну сторону, а равенство P — Q = R, если PnQ направлены в противоположные стороны. В этом случае равнодействующая R направлена в сторону большей силы Р.
Аксиома говорит о сложении сил, приложенных к одной материальной частице, к одной точке. Но складывать силы по правилу параллелограмма можно и в том случае, если они приложены к одному твердому телу и линии их действия пересекаются. В таком случае нужно перенести обе силы в точку пересечения их линий действия и там сложить по правилу параллелограмма, причем если эта точка находится за пределами того тела, на которое действуют обе слагаемые силы, то равнодействующую силу нужно перенести вдоль ее линии действия в какой-либо из точек тела.
Для равновесия трех непараллельных сил, лежащих в одной плоскости, необходимо, чтобы их линии действия пересекались в одной точке
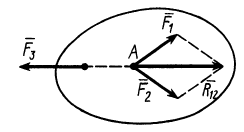
Аксиомы, с которыми мы только что ознакомились, позволяют вывести необходимое условие равновесия трех непараллельных сил: если три непараллельные силы, лежащие в одной плоскости, взаимно уравновешены, то их линии действия пересекаются в одной точке.
Пусть в каких-либо точках А, В и C (рис. 4) к твердому телу, не показанному на чертеже, приложены три силы 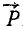
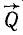
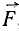
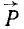
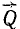
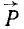
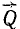
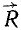
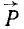
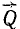
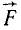
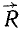
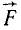
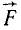
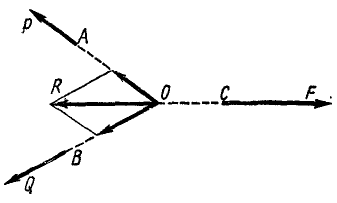
Рис. 4
Это условие равновесия трех сил является необходимым, но не достаточным условием, т. е. если три непараллельные силы находятся в равновесии, то их линии действия обязательно пересекаются в одной точке. Но если линии действия трех сил пересекаются в одной точке, то отсюда вовсе не следует, что эти три силы представляют собой уравновешенную систему сил.
В качестве иллюстрации необходимого условия равновесия трех непараллельных сил приведем такой пример. Для установившегося движения самолета, т. е. чтобы он мог, не теряя набранной высоты, лететь равномерно и прямолинейно, необходимо, чтобы система действующих сил была уравновешенной. Можно считать, что на самолет действуют три силы: его вес, сила тяги и сила сопротивления воздуха (точнее, равнодействующая всех сил сопротивления воздуха, действующих на различные части самолета). Для равновесия этих трех сил необходимо, чтобы их линии действия пересекались в одной точке. Линией действия веса самолета является вертикаль, проходящая через центр тяжести, а сила тяги действует вдоль оси пропеллера. Отсюда вытекает правило, называемое основным правилом самолетостроения: равнодействующая сил сопротивления воздуха должна пересекать ось пропеллера в той же точке, где ее пересекает вертикаль, проходящая через центр тяжести самолета.
«Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга всегда между собой равны и направлены в противоположные стороны» (Ньютон)
Принцип равенства действия и противодействия. Силы, приложенные к данному телу, вызываются другими материальными телами. Отдельно от материальных тел, независимо от них, сил в природе не существует. Поясним это следующим примером.
Представим себе, что санки C скользят по ледяной горе AB (рис. 5). На санки действуют следующие силы: сила тяжести 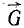
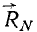
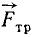
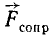
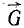
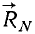
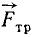
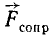
Но действия материальных тел не бывают односторонними, они всегда взаимны, тела взаимодействуют между собой.
В рассмотренном примере на санки действует сила 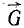
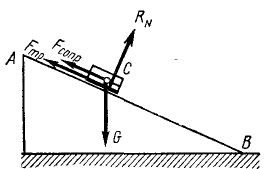
Рис. 5
Аксиома утверждает, что действия двух тел друг на друга равны и противоположны. В нашем примере согласно этой аксиоме Земля притягивает к себе санки с такой же, но обратно направленной силой, с какой санки притягивают Землю; давление санок на гору равно и противоположно давлению горы на санки, силы трения санок о гору и горы о санки равны и противоположны, а воздух сопротивляется движению санок с силой, равной и противоположной той, с которой санки действуют на воздух.
Таких примеров можно привести сколь угодно много и на каждом из них убедиться, что силы, с которыми два тела действуют друг на друга, равны и противоположны.
Нужно твердо усвоить, что механические взаимодействия двух тел хотя и равны по величине и противоположны по направлению и действуют по одной прямой, но не уравновешивают друг друга, так как они приложены не к одному, а к разным телам. Давление или притяжение одного тела может привести в движение другое тело именно потому, что действие и. противодействие приложены к двум различным телам.
Если, например, буксирный теплоход тянет на канате баржу, то и баржа тянет буксир в обратном направлении с равной силой. В этом можно убедиться, прикрепив на обоих концах каната по динамометру, чтобы один из них измерял силу, с которой буксир тянет баржу, а другой — силу, с которой баржа противодействует буксиру. Показания обоих динамометров будут одинаковы. Следовательно, действие буксира на баржу равно и противоположно действию баржи на буксир. Почему же в таком случае вся система перемещается в сторону буксира, а не в обратном направлении? Ответ на этот вопрос очевиден: буксир отталкивается от воды винтом или гребными колесами. По той же аксиоме этой силе, приложенной к шлицам гребного колеса, соответствует другая, равная и противоположная сила, приложенная к воде. Обе эти силы не уравновешивают друг друга, поскольку они не приложены к одному телу.
Приложенная к буксиру сила, с которой он отталкивается от воды, при ускоренном движении больше той силы, также приложенной к буксиру, с которой тянет его назад баржа, при замедленном—меньше, при равномерном движении и при покое — равна. Но всегда — и в покое, и во всяком движении — взаимодействия гребных колес и воды равны и противоположны между собой, и всегда действие буксира на баржу равно и противоположно действию баржи на буксир. Действию всегда есть равное и противоположное противодействие.
Эту аксиому называют принципом равенства действия и противодействия. Она сформулирована Ньютоном, принята им в качестве третьего основного закона механики и опубликована в книге «Математические начала натуральной философии».
Равновесие нетвердого тела не нарушится, если это тело затвердеет
Аксиома затвердения
Если какое-либо нетвердое тело находится в равновесии под действием некоторой системы сил, то можно предположить, что другое. тождественное пo форме, но абсолютно твердое тело под действием такой же системы сил тоже должно быть в равновесии. Аксиома утверждает, что от затвердения равновесие нетвердого тела не нарушится. В статике встречаются задачи о равновесии тела, состоящего из нескольких твердых тел, так или иначе связанных («сочлененных») между собой. Такое тело находится в равновесии, если в равновесии находятся все составляющие его тела. В некоторых случаях такое тело рассматривают как затвердевшее, т. е. как одно абсолютно твердое тело.
Обратим внимание на то, что обратное утверждение является неправильным, т. е. нельзя утверждать, что равновесие твердого тела обязательно сохранится, если это тело перестанет быть твердым.
Что нужно знать о статике
В результате изучения раздела «Статика» необходимо уметь складывать силы, определять равнодействующую любого числа данных сил. Нужно уметь также решить и обратную задачу — данную силу разложить на две или три составляющих.
Главное место в статике занимает учение о равновесии систем сил. Системой называется совокупность сил, приложенных к телу или к точке.
Для удобства изучения системы сил разделяются на плоские и пространственные. В свою очередь плоские системы сил делятся на три группы: а) системы сил, сходящихся в одной точке; б) системы параллельных сил и в) системы сил, расположенных в плоскости как угодно. На аналогичные три группы делятся и пространственные системы сил.
В соответствии с этим дальнейшее изложение методов и примеров решения задач проведено по этой классификации систем сил.
Для любой плоской, а также и пространственной системы сил показаны способы и методы сложения сил и, в частности, определения их равнодействующей силы. В главе II «Плоская система сходящихся сил» показаны способы разложения силы на две составляющие; в главе IV «Пространственная система сил» показан способ разложения силы на три составляющие вдоль трех взаимно перпендикулярных осей. Наиболее широко рассмотрены задачи на равновесие сил, при решении которых используются условия равновесия всех перечисленных выше систем сил.
При решении задач необходимо иметь в виду, что с I января 1963 г. в СССР введена в действие Международная система единиц (ГОСТ 9867 —61), или сокращенно СИ (интернациональная система).
В настоящее время осуществляется переход всех измерений и технических расчетов на эту систему.
Международная система (СИ) имеет шесть основных единиц и две дополнительные. Из основных только три непосредственно применяются в теоретической механике:
Если в известную из физики формулу второго закона Ньютона
вместо массы т и ускорения а подставить единицы их измерения — соответственно 1 кг и 1 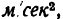
Иными словами, ныотон — это сила, сообщающая единице массы (1 кг) единицу ускорения
Если в условии задачи задана масса нагрузки, то необходимо определить ее вес G:
где 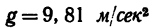
В технической системе единиц (в системе МКГСС) сила измеряется в килограммах
Соотношение между 1 н и 1 кГ таково:
1 н = 0,102 кГ и 1 кГ = 9,81 н.
При приближенных расчетах можно пользоваться округленными соотношениями:
Общую формулу перехода от единиц технической системы (Т кГ) к единицам СИ (S н) можно выразить так:
Соответственно формула перехода от единиц СИ (S н) к единицам технической системы (Т кГ) выразится в виде
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.