На чем основан алгоритм сжатия jpeg
АЛГОРИТМЫ СЖАТИЯ
Алгоритм JPEG
JPEG – достаточно мощный алгоритм. Практически он является стандартом де-факто для полноцветных изображений. Оперирует алгоритм областями 8×8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого, при разложении матрицы такой области в двойной ряд по косинусам значимыми оказываются только первые коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет плавности изменения цветов в изображении.
Алгоритм разработан группой экспертов в области фотографии специально для сжатия 24-битных изображений. JPEG – Joint Photographic Expert Group – подразделение в рамках ISO – Международной организации по стандартизации. Название алгоритма читается [‘jei’peg]. В целом алгоритм основан на дискретном косинусоидальном преобразовании – ДКП (Discrete-Cosine Transform – DCT), применяемом к матрице изображения для получения некоторой новой матрицы коэффициентов. Для получения исходного изображения применяется обратное преобразование.
ДКП раскладывает изображение по амплитудам некоторых частот. Таким образом, при преобразовании мы получаем матрицу, в которой многие коэффициенты либо близки, либо равны нулю. Кроме того, благодаря несовершенству человеческого зрения, можно аппроксимировать коэффициенты более грубо без заметной потери качества изображения.
Для этого используется квантование коэффициентов (quantization). В самом простом случае – это арифметический побитовый сдвиг вправо. При этом преобразовании теряется часть информации, но может достигаться большая степень сжатия.
Как работает алгоритм
Рассмотрим алгоритм подробнее. Пусть мы сжимаем 24-битное изображение.
Шаг 1.
Переводим изображение из цветового пространства RGB, с компонентами, отвечающими за красную (Red), зеленую (Green) и синюю (Blue) составляющие цвета точки, в цветовое пространство YCrCb (иногда называют YUV). В нем Y – яркостная составляющая, а Cr, Cb — компоненты, отвечающие за цвет (хроматический красный и хроматический синий). За счет того, что человеческий глаз менее чувствителен к цвету, чем к яркости, появляется возможность архивировать массивы для Cr и Cb компонент с большими потерями и, соответственно, большими степенями сжатия. Подобное преобразование уже давно используется в телевидении. На сигналы, отвечающие за цвет, там выделяется более узкая полоса частот.
Упрощенно перевод из цветового пространства RGB в цветовое пространство YCrCb можно представить с помощью матрицы перехода:
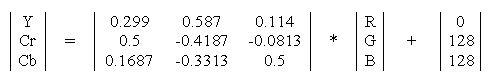 |
Обратное преобразование осуществляется умножением вектора YUV на обратную матрицу:
 |
Шаг 2.
Разбиваем исходное изображение на матрицы 8×8. Формируем из каждой три рабочие матрицы ДКП – по 8 бит отдельно для каждой компоненты. При больших степенях сжатия этот шаг может выполняться чуть сложнее. Изображение делится по компоненте Y – как и в первом случае, а для компонент Cr и Cb матрицы набираются через строчку и через столбец. Т.е. из исходной матрицы размером 16×16 получается только одна рабочая матрица ДКП. При этом, как нетрудно заметить, мы теряем 3/4 полезной информации о цветовых составляющих изображения и получаем сразу сжатие в два раза. Мы можем поступать так благодаря работе в пространстве YCrCb. На результирующем RGB изображении, как показала практика, это сказывается несильно.
Шаг 3.
В упрощенном виде ДКП при n=8 можно представить так:
 |
Применяем ДКП к каждой рабочей матрице. При этом мы получаем матрицу, в которой коэффициенты в левом верхнем углу соответствуют низкочастотной составляющей изображения, а в правом нижнем – высокочастотной. Понятие частоты следует из рассмотрения изображения как двумерного сигнала (аналогично рассмотрению звука как сигнала). Плавное изменение цвета соответствует низкочастотной составляющей, а резкие скачки – высокочастотной.
Шаг 4.
Производим квантование. В принципе, это просто деление рабочей матрицы на матрицу квантования поэлементно. Для каждой компоненты (Y, U и V), в общем случае, задается своя матрица квантования q[u,v] (далее МК).
 |
На этом шаге осуществляется управление степенью сжатия, и происходят самые большие потери. Понятно, что, задавая МК с большими коэффициентами, мы получим больше нулей и, следовательно, большую степень сжатия. В стандарт JPEG включены рекомендованные МК, построенные опытным путем. Матрицы для большей или меньшей степени сжатия получают путем умножения исходной матрицы на некоторое число gamma.
С квантованием связаны и специфические эффекты алгоритма. При больших значениях коэффициента gamma потери в низких частотах могут быть настолько велики, что изображение распадется на квадраты 8×8. Потери в высоких частотах могут проявиться в так называемом » эффекте Гиббса», когда вокруг контуров с резким переходом цвета образуется своеобразный «нимб».
Шаг 5.
Переводим матрицу 8×8 в 64-элементный вектор при помощи «зигзаг»-сканирования, т.е. берем элементы с индексами (0,0), (0,1), (1,0), (2,0).
 |
Таким образом, в начале вектора мы получаем коэффициенты матрицы, соответствующие низким частотам, а в конце — высоким.
Шаг 6.
Свертываем вектор с помощью алгоритма группового кодирования. При этом получаем пары типа (пропустить, число), где “пропустить” является счетчиком пропускаемых нулей, а “число” – значение, которое необходимо поставить в следующую ячейку. Так, вектор 42 3000-2 00001. будет свернут в пары (0,42) (0,3) (3,-2) (4,1).
Шаг 7.
Свертываем получившиеся пары кодированием по Хаффману с фиксированной таблицей.
Процесс восстановления изображения в этом алгоритме полностью симметричен. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь.
Конвейер операций, используемый в алгоритме JPEG:
 |
Не очень приятным свойством JPEG является также то, что нередко горизонтальные и вертикальные полосы на дисплее абсолютно не видны и могут проявиться только при печати в виде муарового узора. Он возникает при наложении наклонного растра печати на горизонтальные и вертикальные полосы изображения. Из-за этих сюрпризов JPEG не рекомендуется активно использовать в полиграфии, задавая высокие коэффициенты матрицы квантования. Однако при архивации изображений, предназначенных для просмотра человеком, он на данный момент незаменим.
Широкое применение JPEG долгое время сдерживалось, пожалуй, лишь тем, что он оперирует 24-битными изображениями. Поэтому для того, чтобы с приемлемым качеством посмотреть картинку на мониторе в 256-цветной палитре, требовалось применение соответствующих алгоритмов и, следовательно, определенное время. В приложениях, ориентированных на придирчивого пользователя, таких, например, как игры, подобные задержки неприемлемы. Кроме того, если имеющиеся изображения, допустим, в 8-битном формате GIF перевести в 24-битный JPEG, а потом обратно в GIF для просмотра, то потеря качества произойдет дважды при обоих преобразованиях. Тем не менее, выигрыш в размерах архивов зачастую настолько велик (в 3-20 раз), а потери качества настолько малы, что хранение изображений в JPEG оказывается очень эффективным.
Стандартизован JPEG в 1991 году. Но уже тогда существовали алгоритмы, сжимающие сильнее при меньших потерях качества. Дело в том, что действия разработчиков стандарта были ограничены мощностью существовавшей на тот момент техники.
Несколько слов необходимо сказать о модификациях этого алгоритма. Хотя JPEG и является стандартом ISO, формат его файлов не был зафиксирован. Пользуясь этим, производители создают свои, несовместимые между собой форматы, и, следовательно, могут изменить алгоритм. Так, внутренние таблицы алгоритма, рекомендованные ISO, заменяются ими на свои собственные. Кроме того, легкая неразбериха присутствует при задании степени потерь. Например, при тестировании выясняется, что «отличное» качество, “100%” и “10 баллов” дают существенно различающиеся картинки. При этом, кстати, «100%» качества не означают сжатие без потерь. Встречаются также варианты JPEG для специфических приложений.
Характеристики алгоритма JPEG:
Степень сжатия 2-200 (Задается пользователем).
Класс изображений: Полноцветные 24 битные изображения или изображения в градациях серого без резких переходов цветов (фотографии).
Симметричность: 1
Характерные особенности: В некоторых случаях, алгоритм создает «ореол» вокруг резких горизонтальных и вертикальных границ в изображении (эффект Гиббса). Кроме того, при высокой степени сжатия изображение распадается на блоки 8×8 пикcелей.
Русские Блоги
Подробное объяснение принципа сжатия JPEG
Шаг 1. Сегментация изображения
На первом этапе алгоритма JPEG изображение разделяется на маленькие блоки 8X8, которые обрабатываются индивидуально в течение всего процесса сжатия. Позже мы возьмем в качестве примера очень классический снимок. Этот снимок называется «Ленна». Говорят, что это первое изображение в формате JPG в мире. С момента своего рождения эта картинка связана с обработкой изображений и сопровождала бесчисленное количество людей. Бессонные ночи, проведенные ботаником науки и техники, можно охарактеризовать как выдающиеся достижения. Заинтересованные друзья могут посетитьВотУзнайте историю этой картины.

Шаг 2: преобразование цветового пространства RGB-> YCbCr
Так называемое «Цветовое пространство«Относится к математической модели, которая выражает цвета. Например, наша общая модель« RGB »разлагает цвета на три компонента: красный, зеленый и синий, так что изображение может быть разложено на три изображения в градациях серого. В математическом выражении каждое Шаблон 8X8 может быть выражен в виде трех матриц 8X8, диапазон значений которых обычно находится между [0,255].
 | (1.1) |
|---|
По опыту КР = 0,299, КБ = 0,114, тогда
 | (1.2) |
|---|
Определение разницы в цвете между синим и красным выглядит следующим образом.
 | (1.3) |
|---|
 | (1.4) |
|---|
Наконец, математическая формула для преобразования RGB в YCbCr может быть получена как
 | (1.5) |
|---|
Модель YCbCr широко используется при сжатии и передаче изображений и видео.Например, вы можете обратить внимание на интерфейс за телевизором или DVD, и вы можете найти интерфейс разницы цветов.


Хорошо видно, что на карте яркости больше деталей. После того, как JPEG преобразует изображение в YCbCr, может выполняться различная обработка в зависимости от важности данных. Вот почему JPEG использует это цветовое пространство.
Шаг 3: дискретное косинусное преобразование
 |  |
|---|
 | (2.1) |
|---|
В это время исходные данные Xi могут быть выражены с помощью обратного преобразования дискретного косинусного преобразования (IDCT)
 | (2.2) |
|---|
Другими словами, после преобразования DCT массив может быть разложен на сумму нескольких массивов. Если наш массив рассматривается как одномерная матрица, то результат можно рассматривать как сумму ряда матриц.
 | (2.3) |
|---|
 [50,55,67,80,-10,-5,20,30] | |
|---|---|
| Массив 0 |  |
| [35.9,35.9,35.9,35.9,35.9,35.9,35.9,35.9] | |
| Массив 1 |  |
| [26.0,22.1,14.8,5.2,-5.2,-14.8,-22.1,-26.1] | |
| Массив 2 |  |
| [3.3,1.4,-1.4,-3.3,-3.3,-1.4,1.4,3.3] | |
| Массив 3 |  |
| [-23.0,5.4,27.2,15.4,-15.4,-27.2,-5.4,23.0] | |
| Массив 4 |  |
| [1.6,-1.6,-1.6,1.6,1.6,-1.6,-1.6,1.6] | |
| Массив 5 |  |
| [9.1,-16.1,3.2,13.6,-13.6,-3.2,16.1,-9.1] | |
| Массив 6 |  |
| [-0.8,1.9,-1.9,0.8,0.8,-1.9,1.9,-0.8] | |
| Массив 7 |  |
| [-2.1,6.1,-9.1,10.8,-10.8,9.1,-6.1,2.1] |
Насколько мощна DCT? Мы можем провести реальный тест, например, матрицу со всеми одинаковыми значениями. После преобразования DCT все уровни массивов объединяются в новую матрицу.
Видно, что после изменения DCT данные, очевидно, делятся на две части: компонент постоянного тока и компонент переменного тока, которые полностью открывают путь для дальнейшего сжатия. Можно сказать, что это самый важный шаг во всем JPEG. Мы представим данные позже. Определить количественно.
Шаг 4: количественная оценка данных
 | (3.1) |
|---|
Таблица квантования стандартной яркости
Стандартная таблица квантования цветового различия
Среди них функция округления является функцией округления, но при этом учитывается округление, что означает
 | (3.2) |
|---|
Следующая работа состоит в том, чтобы снова выполнить сжатие Хаффмана на этом массиве и получить окончательные сжатые данные.
Шаг пятый: кодирование Хавермана
Последним шагом сжатия JPEG является кодирование данных Хаффманом (Huffman coding), Хаффман является основой почти всех алгоритмов сжатия.Его основной принцип заключается в корректировке длины кодирования элементов в соответствии с частотой использования элементов в данных для получения более высокой степени сжатия.
Возьмем пример, такой как следующий фрагмент данных «AABCBABBCDBBDDBAABDBBDABBBBDDEDBD»
Этот фрагмент данных содержит 33 символа. Каждый символ встречается следующее количество раз.
Если мы используем нашу обычную кодировку фиксированной длины, каждый символ составляет 3 бита.
Таким образом, для сохранения этого текста требуется всего 3 * 33 = 99 бит, но если мы используем следующую кодировку, основанную на вероятности появления символа
| ①Оригинальные данные | 35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0 |
|---|
* RLE-Run-Length Encoding, то есть кодирование длин серий, имеет хорошую степень сжатия для повторяющихся символов. После кодирования это (количество вхождений знаков, знаков).
На самом деле в JPEG используется (количество вхождений символов-1, символов)
| Length | Value | Bits |
|---|---|---|
| 3 bits | 04 05 03 02 06 01 00 (EOB) | 000 001 010 011 100 101 110 |
4 bits 07 1110 5 bits 08 1111 0 6 bits 09 1111 10 7 bits 0A 1111 110 8 bits 0B 1111 1110
| Length | Value | Bits |
|---|---|---|
| 2 bits | 01 02 | 00 01 |
3 bits 03 100 4 bits 00 (EOB)
04
11 1010
1011
1100 5 bits 05
12
21 1101 0
1101 1
1110 0 6 bits 31
41 1110 10
1110 11 … … … 12 bits 24
33
62
72 1111 1111 0100
1111 1111 0101
1111 1111 0110
1111 1111 0111 15 bits 82 1111 1111 1000 000 16 bits 09
…
FA 1111 1111 1000 0010
…
1111 1111 1111 1110
После кодирования и сериализации Хаффмана окончательные данные приобретают следующий вид
В итоге мы использовали 10 байт для сохранения исходной длины массива из 64. На данный момент основной алгоритм сжатия JPEG завершен. Эти данные являются окончательными данными, сохраненными в файле jpg.
Анализ примера изображения JPEG
Мы можем открыть файл JPEG для просмотра содержимого внутри, а затем мы сможем увидеть различные сегменты маркера выше:
В заголовке есть FFD8, что означает начало изображения; FFD9 в конечной части, что означает конец изображения.
Посередине находятся две метки FFDB, соответствующие таблице квантования DQT;
Также есть FFC0, соответствующий информации о размере изображения.
Сзади есть четыре таблицы Хаффмана, соответствующие FFC4;
Как правило, в файле JPEG есть два типа таблиц Хаффмана: одна для постоянного тока и одна для переменного тока, то есть на самом деле существует 4 таблицы: постоянный и переменный ток для яркости и постоянный и переменный ток для цветности.
Затем сегмент данных изображения помечается как FFDA;
Давайте рассмотрим детали каждого знака и подробно проанализируем значение каждой части.
1. Информация для идентификации изображения
SOI, начало изображения, начало изображения, 2 байта, фиксированное значение 0xFFD8
JEPG APP0 Приложение зарезервировано, отметка 0
Имя поля
Длина поля
Comments
Маркер кода маркера
Фиксированное значение 0xFF, 0xE0
Длина данных Длина
Общая длина APP0, не включая маркер, но включая саму длину
Фиксированная строка «JFIF \ 0»
Обычно 0x0101 или 0x0102,Указывает номер версии JFIF 1.1 или 1.2.
Единица измерения пикселей
Единица координат, 0 без единицы; 1 пиксель / дюйм; 2 пикселя / см
Количество пикселей по горизонтали X плотность
Диапазон значений неизвестен
Количество пикселей по вертикали YDensity
Диапазон значений неизвестен
Горизонтальные пиксели эскиза
Диапазон значений неизвестен
Пиксели эскиза по вертикали
Диапазон значений неизвестен
Растровое изображение в формате RGB для эскизов
n = Xthumbnail * Ythumbnail, это растровое изображение RGB 24 бит / кусок xl
Если нет миниатюрного изображения (это чаще всего), поле «Количество миниатюр по горизонтали в пикселях» и поле «Количество миниатюр по вертикали в пикселях» имеют значения 0.
Приведенное выше содержимое после маркировки FFE0 имеет длину 16.
Затем идет 5-байтовый идентификатор JFIF, указывающий, что это сжатый файл JPEG.
Затем плотность пикселей в направлении XY, здесь 96 точек на дюйм, и, наконец, информация об эскизах, здесь 0.
2. Примеры таблиц квантования
То есть содержимое первой таблицы квантования DQT, выраженное в десятичном формате, выглядит следующим образом:
Эта таблица представляет собой таблицу квантования яркости JPEG.
Содержимое второй таблицы квантования:
Когда вы откроете разные файлы JPEG, вы увидите, что эти две таблицы также могут отличаться. В основном это результат использования различных методов количественной оценки.
3. Информационный сегмент изображения
Затем следует точность данных в один байт, обычно 8, который представляет количество выборок.
Далее идет высота изображения, которая занимает два байта, которая здесь равна 8, а затем ширина изображения, которая также равна 8, что мы определили как 8×8.
После этого идет номер таблицы квантования.
4. Пример таблицы Хаффмана.
Вторая таблица DHT, 10, относится к типу таблицы AC, и номер HT ID также равен 0;
В качестве примера возьмем первую таблицу. Поскольку длина всего 31, 16 байтов после 00 являются зеленой частью:
В группе, номер группы которой равен 1, имеется 0 кодов;
Если номер группы 2, есть 1 код;
Имеется 5 кодов с номером группы 3;
Один код для каждой группы номер 4/5/6/7/8/9.
Посмотрите на последующие данные:
00 01 02 03 04 05 06 07 08 09 0A 0B
Для других номеров групп, которые не отображаются, соответствующие данные не используются. Другими словами, в упомянутой ранее парадигме кодирования Хаффмана в настоящее время используется только часть данных, потому что данные изображения 8×8 очень малы.
Вторая таблица DHT более сложная и имеет длину 181.
5. Сегмент данных изображения
Здесь сегмент SOS имеет длину 12, а количество компонентов, содержащихся в задней части, равно 3, что составляет Y UV. Затем следуют номер каждого компонента и идентификатор соответствующей таблицы Хаффмана.




















