1. На чем основан принцип измерения физических величин?

А) на применении измерительных приборов;
Б) на сравнении измеряемой величины с эталонным значением;
В) на умении пользоваться измерительными приборами;
Г) на умении определять цену деления прибора.
2. Поезд длиной 200 м выезжает на мост длиной 400 м. Скорость поезда равна 36 км/ч. Определите время движения поезда по мосту.
А) 1 мин; Б) 40 с; В) 2 мин; Г) 90 с.
3. Масса одного кубика равна 800 г. Как изменилась масса кубика, если его ребро уменьшилось в 2 раза?
А) уменьшилась в 2 раза; Б) уменьшилась в 4 раза;
В) уменьшилась в 8 раз; Г) уменьшилась в 16 раз.
4. Плотность вещества равна 0,002 г/мм3. Чему равна эта плотность в кг/м3?
А) 20 кг/м3; Б) 2000 кг/м3;
В) 2 кг/м3; Г) 200 кг/м3.
5. Тело выезжает на шероховатый участок, и на него начинает действовать сила трения в 10 Н. Пойдя 6 м, тело останавливается. Чему равна работа с
7. На рисунке показан рычаг, к которому в точке А приложена сила F1= 4 Н. Какую силу F2 нужно приложить к точке В, чтобы рычаг находился в равновесии?
А) 4 Н;
Б) 2 Н;
В) 6 Н;
Г) 8 Н.

8. Какой простой механизм изображен на рисунке?
А) подвижный блок;
Б) ворот;
В) рычаг;
Г) неподвижный блок.
9. КПД наклонной плоскости равен 42%. При поднятии по ней груза совершили работу в 400 Дж. Чему равна полезная работа в этом процессе?
А) 160 Дж; Б) 1000 Дж; В) 400 Дж; Г) 200 Дж.
10. Диаметр молекул равен 2•10-7 см. Какое количество молекул нужно уложить в ряд, чтобы длина цепочки была 1 мм?
А) 5000; В) 500000;
Б) 50000; Г) 500.
11. Масса автомобиля «Жигули» равна 900 кг, а площадь соприкосновения шины с дорогой равна 225 см2. Какое давление оказывает автомобиль на дорогу?
А) 1000 Па; В) 100 Па;
Б) 10000 Па; Г) 100000 Па.
12. В цилиндрический сосуд налили воду до высоты 40 см. До какой высоты нужно налить в другой такой же сосуд керосин, чтобы давление на дно было таким же, как и в первом сосуде? Плотность воды 1 г/см3, керосина – 0,8 г/см3.
А) 50 см; Б) 30 см; В) 60 см; Г) 45 см.
13. Гидравлический пресс имеет поршни с площадью S1= 200 см2 и S2= 1500 см2. На меньший поршень действует сила 100 Н. Какая сила возникает на большом поршне?
А) 500 Н; В) 1000 Н;
Б) 750 Н; Г) 800 Н.
14. В сосуд с водой положили три шарика одинаковой массы: сосновый, алюминиевый и железный. На какой из шариков действует самая большая и самая маленькая сила Архимеда? ρ1= 400 кг/м3, ρ2= 2700 кг/м3, ρ3= 7800 кг/м3.
А) FA1= min, FA3 = max; В) FA2 = min, FA3 = max;
Б) FA3 = min, FA2 = max; Г) FA3 = min, FA1 = max.
15. Пробку массой 100 г опустили на поверхность керосина. Чему равна сила Архимеда, действующая на пробку? ρП = 200 кг/м3, ρК = 800 кг/м3.
А) 1 Н; Б) 2 Н; В) 3 Н; Г) 4 Н.
16. У плавающей льдины над водой находится объем 2 м3. Чему равна масса всей льдины? Плотность воды 1000 кг/м3, льда 900 кг/м3.
А) 20000 кг; В) 10000 кг;
Б) 18000 кг; Г) 30000 кг.
17. В сосуде с водой плавает кусок льда. Как изменится уровень воды в сосуде, если лед растает?
А) уменьшится; В) не изменится;
Б) увеличится; Г) зависит от формы сосуда.
18. Подъемная сила шара, заполненного гелием, равна 600 Н. Чему равен объем шара, если плотность гелия 0,2 кг/м3, плотность воздуха 1,3 кг/м3.
А) 5 м3; Б) 30 м3; В) 50 м3; Г) 60 м3.

Источник

Лекция 2. Виды и методы измерений

Описание

1. Основные понятия и определения. Виды измерений.

2. Методы измерений.

3. Понятие о точности измерений.

4. Основы обеспечения единства измерений

Оглавление

1. Основные понятия и определения. Виды измерений

Измерение — совокупность операций по применению системы измерений для получения значения измеряемой физической величины.

Измерения могут быть классифицированы по метрологическому назначению на три категории:

Ненормированные – измерения при ненормированных метрологических характеристиках.

Технические – измерения при помощи рабочих средств измерений.

Метрологические – измерения при помощи эталонов и образцовых средств измерений.

Ненормированные измерения наиболее простые. В них не нормируются точность и достоверность результата. Поэтому область их применения ограничена. Они не могут быть применены в области, на которую распространяется требование единства измерений. Каждый из нас выполнял ненормированные измерения длины, массы, времени, температуры не задумываясь о точности и достоверности результата. Как правило, результаты ненормированных измерений применяются индивидуально, т.е. используются субъектом в собственных целях.

Технические измерения удовлетворяют требованиям единства измерений, т.е. результат бывает получен с известной погрешностью и вероятностью, записывается в установленных единицах физических величин, с определённым количеством значащих цифр. Выполняются при помощи средств измерений с назначенным классом точности, прошедших поверку или калибровку в метрологической службе. В зависимости от того, предназначены измерения для внутрипроизводственных целей или их результаты будут доступны для всеобщего применения, необходимо выполнение калибровки или поверки средств измерений. Средство измерений, прошедшее калибровку или поверку, называют рабочим средством измерений. Примером технических измерений является большинство производственных измерений, измерение квартирными счётчиками потреблённой электроэнергии, измерения при взвешивании в торговых центрах, финансовые измерения в банковских терминалах. Средство измерений, применяемое для калибровки других средств измерений, называют образцовым средством измерений. Образцовое средство измерений имеет повышенный класс точности и хранится отдельно, для технических измерений не применяется.

Метрологические измерения не просто удовлетворяют требованиям единства измерений, а являются одним из средств обеспечения единства измерений. Выполняются с целью воспроизведения единиц физических величин для передачи их размера образцовым и рабочим средствам измерений. Метрологические измерения выполняет метрологическая служба в стандартных условиях, сертифицированным персоналом.

В дисциплине «Метрология, стандартизация и сертификация» рассматриваются технические измерения.

Можно выделить следующие виды измерений.

1) По характеру зависимости измеряемой величины от времени методы измерений подразделяются на:

2) По способу получения результатов измерений (виду уравнений измерений) методы измерений разделяют на прямые, косвенные, совокупные и совместные.

При прямом измерении искомое значение величины находят непо­средственно из опытных данных (например, измерение диаметра штан­генциркулем).

При косвенном измерении искомое значение величины определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

Совместными называют измерения двух или нескольких не одноимённых величин, производимые одновременно с целью нахождения функциональной зависимости между величинами (например, зависимости длины тела от температуры).

Совокупные – это такие измерения, в которых значения измеряемых величин находят по данным повторных измерений одной или нескольких одноименных величин (при различных сочетаниях мер или этих величин) путем решения системы уравнений.

3) По условиям, определяющим точность результата измерения, мето­ды делятся на три класса.

Измерении максимально возможной точности (например, эталонные измерения), достижимой при существующем уровне техники.

Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторое заданное значение.

Технические измерения, в которых погрешность результата определяется характеристиками средств измерения.

4) По способу выражения результатов измерений различают абсолютные и относительные измерения.

Абсолютное измерение основано на прямых измерениях величины и (или) использования значений физических констант.

При относительных измерениях величину сравнивают с одноименной, играющей роль единицы или принятой за исходную (например, измерение диаметра вращающейся детали по числу оборотов соприкасающегося с ней аттестованного ролика).

5) В зависимости от совокупности измеряемых параметров изделия различают поэлементный и комплексный методы измерения.

Поэлементный метод характеризуется измерением каждого параметра изделия в отдельности (например, эксцентриситета, овальности, огранки цилиндрического вала).

Комплексный метод характеризуется измерением суммарного пока­зателя качества (а не физической величины), на который оказывают влияние отдельные его составляющие (например, измерение радиального биения цилиндрической детали, на которое влияют эксцентриситет, овальность и др.).

2. Методы измерений

Метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализо­ванным принципом измерений. Можно выделить следующие методы из­мерений.

По способу получения значения измеряемых величин различают два основных метода измерений.

Метод непосредственной оценки – метод измерения, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия.

Метод сравнения с мерой – метод измерения, при котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.

Разновидности метода сравнения:

При измерении линейных величин независимо от рассмотренных методов различают контактный и бесконтактный методы измерений.

В зависимости от измерительных средств, используемых в процессе измерения, различают:

3. Понятие о точности измерений

Точность результата измерения – характеристика качества измерения, отражающая близость к нулю погрешности его результата.

Эти погрешности являются следствием многих причин: несовершенства средств измерений, метода измерений, опыта оператора; недостаточной тщательности проведения измерения; воздействия внешних условий и т.д. Для оценки степени приближения результатов измерения к истинному значению измеряемой величины используются методы теории вероятности и математической статистики, что позволяет с определенной достоверностью оценить границы погрешностей, за пределы которых они не выходят. Это дает возможность для каждого конкретного случая выбрать средства и методы измерения, обеспечивающие измерение результата, погрешности которого не превышают заданных границ с требуемой степенью доверия к результатам измерений (достоверностью).

Класс точности – обобщённая метрологическая характеристика средства измерения.

Класс точности определяется и обозначается по-разному. Наибольшее распространение получили три варианта, каждый представляет собой выраженное в процентах значение относительной погрешности:

– относительно измеренного значения (относительная погрешность),

– относительно максимального значения шкалы (приведённая погрешность),

– относительно участка шкалы (приведённая к участку шкалы погрешность).

Рассмотрим эти три варианта.

Вариант 1. Относительная погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, результат измерения умножают на класс точности и делят на сто, чтобы избавиться от процентов. Например, вольтметром класса точности 0,1 получено значение 10,000 В.

Абсолютная погрешность составит: (10,000 В ∙ 0,1 %) / 100 % = 0,010 В. Запись результата: (10,000 ± 0,010) В, с вероятностью 95 % (эта вероятность по умолчанию назначается для технических измерений, исходя из этой вероятности определяется и класс точности). При нормировании по относительной погрешности, значение класса точности заключают в кружок. Как правило, обозначение класса точности размещают в правом нижнем углу на шкале средства измерений.

Вариант 2. Приведённая погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, максимальное значение шкалы умножают на класс точности и делят на сто, чтобы избавиться от процентов. Например, вольтметром класса точности 0,1 получено значение 10,000 В. Максимальное значение шкалы составляет 20,000 В.

Абсолютная погрешность составит: (20,000 В ∙ 0,1 %) / 100 % = 0,020 В. Запись результата: (10,000 ± 0,020) В, с вероятностью 95 %. При нормировании по приведённой погрешности, значение класса точности не сопровождают никакими знаками.

Вариант 3. Приведённая к участку шкалы погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, размер участка шкалы умножают на класс точности и делят на сто, чтобы избавиться от процентов. Рассмотрим два примера, для случая, когда вся шкала поделена на два участка.

Пример 1. Участок шкалы от 0,000 В до 12,000 В, отмечен галочкой. Вольтметром класса точности 0,1 получено значение 10,000 В.

Абсолютная погрешность составит: (12,000 В ∙ 0,1 %) / 100 % = 0,012 В. Запись результата: (10,000 ± 0,012) В, с вероятностью 95 %.

Пример 2. Участок шкалы от 12,000 В до 20,000 В, также отмечен галочкой. Вольтметром класса точности 0,1 получено значение 15,000 В.

Абсолютная погрешность составит: (8,000 В ∙ 0,1 %) / 100 % = 0,008 В. Запись результата: (15,000 ± 0,008) В, с вероятностью 95 %. При нормировании по приведённой к участку шкалы погрешности, значение класса точности помещают над галочкой. Участки шкалы, относительно которых нормируется погрешность, обозначают галочками.

Варианты классов точности обусловлены отличием конструктивных, системных и схемотехнических решений средств измерений.

Корректная запись результатов

Запись результатов измерений производится по следующим правилам.

1) Погрешность указывается двумя значащими цифрами, если первая равна 1 или 2. Погрешность указывается одной значащей цифрой, если первая равна 3 или более. Все остальные цифры должны быть не значащими.

Значащей цифрой называется любая цифра числа, записанного в виде десятичной дроби, начиная слева с первой отличной от нуля цифры, независимо от того, где она находится – до запятой или после запятой.

2) Результат измерения округляется в соответствии с его погрешностью, т.е. записывается с той же точностью, что и погрешность.

Рассмотрим пример. Результат измерения: 10,645701, погрешность 0,012908.

1) Рассматриваем погрешность. Первая значащая цифра 1, поэтому оставляем две значащие цифры, округляя, записываем: 0,013.

2) Рассматриваем результат измерения. Погрешность записана с точностью до третьего знака после запятой, поэтому в результате также оставим три знака. Округляя, записываем: 10,646.

Корректная запись: 10,646 ± 0,013.

Корректная запись обеспечивает адекватность и сопоставимость результатов различных измерений и является одним из элементов единства измерений. Как правило, отбрасывание избыточных цифр не приводит к дополнительной погрешности, поскольку избыточные цифры обусловлены точностью вычислений, а не точностью измерений.

4. Основы обеспечения единства измерений

Специализация и кооперирование производства в масштабах страны, основанные на принципах взаимозаменяемости, требуют обеспечения и сохранения единства измерений.

Обеспечение единства измерений – деятельность метрологических служб, направленная на достижение и поддержание единства измерений в соответствии с правилами, требованиями и нормами, установленными государственными стандартами и другими нормативно-техническими документами в области метрологии.

В 1993 г. был принят Закон Российской Федерации «Об обеспечении единства измерений», который устанавливает правовые основы обеспечения единства измерений в нашей стране. Он состоит из семи разделов: общие положения; единицы величин, средства и методики выполнения измерений; метрологические службы; государственный метрологический контроль и надзор; калибровка и сертификация средств измерений; ответственность за нарушение закона и финансирование работ по обеспечению единства измерений. В Законе дано следующее определение понятия «единство измерения»:

«Единство измерения – состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерений не выходят за установленные границы с заданной вероятностью».

Обеспечение единства измерений является задачей метрологических служб.

Метрологическая служба – совокупность субъектов, деятельности и видов работ, направленных на обеспечение единства измерений.

Закон определяет, что Государственная метрологическая служба находится в ведении Госстандарта России и включает: государственные научные метрологические центры; органы Государственной метрологической службы регионов страны, а также городов Москва и Санкт-Петербург.

Источник

Цифровые измерительные приборы: достоинства и недостатки, принцип работы

Цифровые приборы — один из самых революционных способов измерения различных физических величин за всю историю человечества. Можно сказать, что в целом с момента появления цифровых технологий важность этого типа устройств во многом определила будущее всего нашего существования.

Все измерительные приборы подразделяются на аналоговые и цифровые.

Цифровые измерительные приборы обладают высоким быстродействием и высоким классом точности. Они применяются для измерения широкого класса электрических и неэлектрических величин.

В отличии от цифровых аналоговые приборы не хранят измеренные данные и не совместимы с цифровыми микропроцессорными устройствами. По этой причине необходимо записывать каждое проведенное с его помощью измерение, что может быть утомительным и требующим большого количество времени.

Главный недостаток цифровых измерительных приборов заключается в том, что они нуждаются во внешнем источнике питания или подзарядке аккумулятора после определенного времени использования. Также точность, скорость и эффективность цифровых приборов в делают их дороже аналоговых.

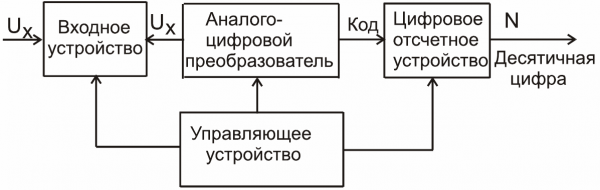
Цифровые измерительные приборы — приборы, в которых измеряемая входная аналоговая величина X автоматически опытным путем сравнивается с дискретными значениями известной (образцовой) величины N и результаты измерения выдаются в цифровом виде (Чем отличаются аналоговые, дискретные и цифровые сигналы).

Структурная схема цифрового вольтметра

При выполнении операций сравнения в цифровых измерительных приборах производится квантование по уровню и времени значений непрерывных измеряемых величин. Результат измерения (численный эквивалент измеряемой величины) образуется после выполнения операций цифрового кодирования и представляется в избранном коде (десятичном для отображения или двоичном для дальнейшей обработки).

Операции сравнения в цифровых измерительных приборах выполняются специальными устройствами сравнения. Обычно конечный результат измерения в таких приборах получается после запоминания и некоторой обработки результатов отдельных операций сравнения аналоговой величины X с различными дискретными значениями образцовой величины N (так же может производиться сравнение известных долей X с N, имеющей одно значение).

Числовой эквивалент X в измерительный прибор представляется с помощью выходных устройств в виде, удобном для восприятия (цифровая индикация), а в необходимых случаях — в виде, удобном для ввода в электронно-вычислительную машину (ЭВМ) или в систему автоматического управления (цифровые регуляторы, программируемые логические контроллеры, интеллектуальные реле, частотные преобразователи). Во втором случае приборы чаще всего называются цировыми датчиками.

В общем случае цифровые измерительные приборы содержат аналогово-цифровые преобразователи, блок формирования образцовой величины N или набор заранее сформированных величин N, устройства сравнения, логические устройства и выходные устройства.

В автоматических цифровых измерительных приборах обязательно наличие устройства, обеспечивающего управление работой его функциональных узлов. Кроме обязательных функциональных блоков прибор может содержать дополнительные, например, преобразователи непрерывных величин X в промежуточные непрерывные величины.

Такие преобразователи используются в измерительных приборах в тех случаях, когда промежуточную X можно более просто измерить, чем исходную. К преобразованиям X в электрические величины прибегают весьма часто при измерении разнообразных неэлектрических величин, в свою очередь, электрические часто представляются эквивалентными интервалами времени и т. д.

Аналого-цифровые преобразователи (АЦП) являются устройствами, которые принимают входные аналоговые сигналы и выдают на выходе соответствующие им цифровые сигналы, пригодные для работы с ЭВМ и другими цифровыми устройствами, т.е. обычно физический сигнал сначала преобразуется в аналоговый (аналогичный по отношению к исходному сигналу), а затем аналоговый сигнал преобразуется в цифровой.

В цифровых измерительных приборах используются различные методы автоматических измерений и измерительные схемы. Наличие дискретных N определяет специфику главным образом способов сравнения.

При методе совпадения обычно используется одновременно несколько устройств сравнений, либо X имеет возможность воздействовать на одно общее устройство, считывающее совпавшее с ним значение N.

Различаются методы следящего, развертывающего и поразрядного уравновешивания, а также методы совпадения со следящим счетом или следящим считыванием, периодическим счетом или периодическим считыванием результатов сравнения.

Первые в истории цифровые измерительные приборы представляли собой системы пространственного кодирования.

В этих приборах (датчиках) в соответствии со схемой измерения измеряемая величина с помощью аналогового преобразователя преобразуется в линейное перемещение или угол поворота.

Далее в аналого-дискретном преобразователе происходит кодирование полученного перемещения или угла поворота при помощи специальной кодовой маски, которая наносится на специальные кодовые диски, барабаны, линейки, пластины, электроннолучевые трубки и т. п.

Маски создают символы (0 или 1) кода числа N в виде проводящих и непроводящих, прозрачных и непрозрачных, магнитных и немагнитных участков и т. п. С этих участков специальные считывающие устройства снимают вводимый код.

Наибольшее распространение получил метод устранения ошибок неоднозначности, основанный на применении специальных циклических кодов, в которых соседние числа отличаются только в одном разряде, т. е. ошибка считывания не может превышать шага квантования. Это достигается за счет того, что при изменении любого числа на единицу в циклическом коде изменяется только один символ (например, используется код Грея).

Источник

Бирюков С., Чередов А. Метрология: Тексты лекций

ОГЛАВЛЕНИЕ

2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ

Прежде чем разбираться в сущности каких-либо явлений, удобно их сначала упорядочить, т.е. классифицировать.

Измерения подразделяются на виды измерений – часть области измерений,

некоторое заданное значение;
— технические, в которых погрешность результата определяется характеристиками средств измерений [11].
По способу выражения результатов измерения различают абсолютные и относительные измерения.
Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительные измерения – измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную [12].

2.2. Методы измерений и их классификация

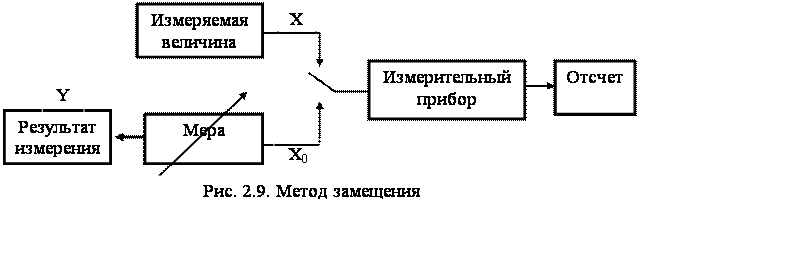
Все измерения могут производиться различными методами. Различают следующие основные методы измерений: метод непосредственной оценки и методы сравнения cмерой [7] .
2.2.1. Метод непосредственной оценки характеризуется тем, что значение измеряемой величины определяется непосредственно по отсчетному устройству измерительного прибора, заранее градуированного в единицах измеряемой величины. Этот метод является наиболее простым и поэтому широко применяется при измерении различных величин, например: измерение веса тела на пружинных весах, силы электрического тока стрелочным амперметром, разности фаз цифровым фазометром и т.д.

Функциональная схема измерения методом непосредственной оценки приведена на рис. 2.3.

Рис. 2.10. Классификация методов измерений

Источник