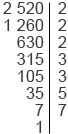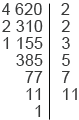На что делится 165

Информация о числах

Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.

Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел.

Сейчас изучают числа:

Число 165

Сто шестьдесят пять

RGB(0, 0, 165) или #0000A5Наибольшая цифра в числе
(возможное основание)6 (7)Число Фибоначчи?НетНумерологическое значение3
детское начало, дружба, радость, позитивность, оптимизм, удача, везение, романтика, общительность, беззаботность, творчествоСинус числа0.9977972794498907Косинус числа-0.06633693633562374Тангенс числа-15.041353046538894Натуральный логарифм5.10594547390058Десятичный логарифм2.2174839442139063Квадратный корень12.84523257866513Кубический корень5.484806552432618Квадрат числа27225Перевод из секунд2 минуты 45 секундДата по UNIX-времениThu, 01 Jan 1970 00:02:45 GMTMD59766527f2b5d3e95d4a733fcfb77bd7eSHA174cbd2c215c2c13c4b6110ada96de8891b355ddaBase64MTY1QR-код числа 165

Описание числа 165

Натуральное целое число 165 является составным числом. 12 — сумма всех цифр. Число имеет следующие делители: 1, 3, 5, 11, 15, 33, 55, 165. Сумма делителей этого числа: 288. Обратное число для 165 — это 0.006060606060606061.
Данное число представляется произведением: 3 * 5 * 11.

Перевод числа 165 в другие системы счисления: двоичная система счисления: 10100101, троичная система счисления: 20010, восьмеричная система счисления: 245, шестнадцатеричная система счисления: A5. 165 байтов представляет из себя число байт 165.

Число 165 — не число Фибоначчи.

Источник

Признаки делимости чисел

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое «признак делимости»

Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.

Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.

Однозначные, двузначные и трехзначные числа

Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.

Трехзначные числа — числа, в составе которых три знака (три цифры).

Чётные и нечётные числа

Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!

Признаки делимости чисел

Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.

Признак делимости на 3. Сумма цифр числа должна делиться на 3.

Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.

Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.

Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.

Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.

Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.

Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.

Источник

Наибольший общий делитель

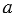
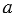
Наибольший общий делитель чисел и обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.

Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.

240 = 2222 3 5 165 = 3 5 11.

Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.

Найдем НОД(2520; 4620).

2 520 = 2 2 2 3 3 5 7 4 620 = 2 2 3 5 7 11.

Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.

Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).

Таким же образом можно найти НОД трех и более чисел.

Чтобы найти НОД нескольких натуральных чисел, надо:

Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.

Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:

2 520 = 2 3 3 2 5 1 7 1

Тогда НОД мы можем найти по следующему правилу:

Найдем НОД(2520; 4620):

Поделись с друзьями в социальных сетях:

Источник

Делитель и кратное в математике

Что такое делители и кратные числа

Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.

Выделяют следующие компоненты деления:

Делимое — число, которое делят на несколько частей.

Делитель — число, которое показывает, на сколько частей нужно разделить делимое.

Частное — число, которое является результатом деления.

Умножение частного на делитель дает делимое.

Чтобы получить делитель, нужно делимое разделить на частное.

Д е л и м о е = ч а с т н о е * д е л и т е л ь Д е л и т е л ь = д е л и м о е / ч а с т н о е

Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.

16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.

Делителем числа a называется такое число b, на которое a делится нацело.

Например, 9 : 4 = 2 (остаток 5 ).

В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.

Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9 : 4 = 2 (остаток 5 ) — число 4 не является делителем числа 9.

Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.

Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.

Тогда представим решение данной задачи в виде уравнения:

72 — целое число, без остатка.

Произведение делителей должно дать в результате 144:

72 * 2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.

Ответ: числа 2 и 72 — делители 144.

Число называют кратным, если оно делится на данное число нацело, без остатка.

Например, 15:3 нацело.

Тогда число 15 является кратным 3.

Слово «кратно» синонимично слову «делится».

Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».

Основные понятия и определения

Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.

Делится нацело = без остатка.

Наименьшим делителем любого числа является единица.

Наибольшим делителем числа является само число.

Делителем нуля будет любое число, но сам 0 делителем не будет.

При делении нуля на любое число получаем 0. А делить на ноль нельзя.

У единицы только один делитель — единица.

Другие числа, кроме 1, имеют не меньше двух делителей.

Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.

Наименьшее кратное числа является равным самому числу.

Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.

Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.

Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.

Чем отличаются друг от друга, как найти

Делитель отличается от кратного тем, что:

Чтобы найти делители числа, нужно данное число разложить на множители.

Разложить на множители — представить число в виде произведения целых чисел.

Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.

Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.

Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.

Примеры решения задач

Необходимо найти делители числа 14.

Решить задание можно двумя способами.

Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.

Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.

Ответ: делители числа 14: 1, 2, 7, 14.

Представим 14 в виде произведения чисел:

Делителями будут множители, так как можем разделить 14 нацело на каждый из них.

Ответ: делители 14: 1, 2, 7, 14.

Найдите три числа, кратных 7.

Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.

7 * 1 = 7 — семь кратно семи;

7 * 2 = 14 — 14 кратно 7;

7 * 3 = 21 — 21 кратно 7.

Ответ: числа, кратные 7: 7, 14, 21.

Самостоятельно проверьте, 225 кратно 3 или нет.

Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.

75 — целое число, при делении нет остатка. Тогда 225 кратно 3.

Найдите любое число, делителями которого являются числа 7 и 8.

Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:

Источник

Наибольший общий делитель

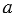
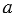
Наибольший общий делитель чисел и обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.

Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.

240 = 2222 3 5 165 = 3 5 11.

Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.

Найдем НОД(2520; 4620).

2 520 = 2 2 2 3 3 5 7 4 620 = 2 2 3 5 7 11.

Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.

Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).

Таким же образом можно найти НОД трех и более чисел.

Чтобы найти НОД нескольких натуральных чисел, надо:

Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.

Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:

2 520 = 2 3 3 2 5 1 7 1

Тогда НОД мы можем найти по следующему правилу:

Найдем НОД(2520; 4620):

Поделись с друзьями в социальных сетях:

Источник