На что делится 280

Обратное число 280 = 0.0035714285714286

Двоичная система счисления 280₂: 100011000

Проверка:

Примеры:

четыре миллиона шестьсот семьдесят четыре тысячи семьсот один плюс двести восемьдесят равно четыре миллиона шестьсот семьдесят четыре тысячи девятьсот восемьдесят один

двести восемьдесят плюс три миллиона сто сорок одна тысяча сто девять равно три миллиона сто сорок одна тысяча триста восемьдесят девять

двести восемьдесят умножить на пятнадцать тысяч пятьсот семьдесят один равно четыре миллиона триста пятьдесят девять тысяч восемьсот восемьдесят

двести восемьдесят плюс семь миллионов шестьдесят три тысячи триста девяносто четыре равно семь миллионов шестьдесят три тысячи шестьсот семьдесят четыре

Есть информация, что Вы сочтете нужным заказать бакалаврская работу недорого у надежного исполнителя. А если еще и со скидкой?

Источник

Информация о числах

Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.

Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел.

Сейчас изучают числа:

Число 280

Двести восемьдесят

RGB(0, 1, 24) или #000118Наибольшая цифра в числе
(возможное основание)8 (9)Число Фибоначчи?НетНумерологическое значение1
мужество, логика, независимость, самостоятельность, индивидуализм, смелость, решительность, изобретательностьСинус числа-0.3878094208292295Косинус числа-0.9217395798793158Тангенс числа0.42073643065214333Натуральный логарифм5.634789603169249Десятичный логарифм2.4471580313422194Квадратный корень16.73320053068151Кубический корень6.542132620377179Квадрат числа78400Перевод из секунд4 минуты 40 секундДата по UNIX-времениThu, 01 Jan 1970 00:04:40 GMTMD592c8c96e4c37100777c7190b76d28233SHA1ba613d1fc0d9300175611e31cca7cf9f525056cbBase64MjgwQR-код числа 280

Описание числа 280

Число 280 в других системах счисления: двоичный вид числа: 100011000, троичный вид числа: 101101, восьмеричный вид числа: 430, шестнадцатеричный вид числа: 118. 280 байтов — столько информации находится в числе байт 280.

Число 280 не является числом Фибоначчи.

Источник

Нахождение всех делителей числа, число делителей числа

В данной статье мы поговорим о том, как найти все делители числа. Начнем с доказательства теоремы, с помощью которой можно задать вид всех делителей определенного числа. Далее возьмем примеры нахождения всех нужных делителей и покажем, как именно определить, сколько делителей имеет конкретное число. В последнем пункте подробно рассмотрим примеры задач на нахождение общих делителей нескольких чисел.

Как найти все делители числа

Сложнее определить все делители составного числа. Сформулируем теорему, которая лежит в основе данного действия.

Учитывая доказательство этой теоремы, мы можем сформировать схему нахождения всех положительных делителей данного числа.

Для этого нужно выполнить следующие действия:

Самым трудным в таком расчете является именно перебор всех комбинаций указанных значений. Разберем подробно решения нескольких задач, чтобы наглядно показать применение данной схемы на практике.

Решение

Для нахождения делителей удобно все полученные значения оформлять в виде таблицы:

Возьмем пример чуть сложнее: в нем при разложении числа получится не один, а два множителя.

Решение

Начнем с разложения данного числа на простые множители.

567 189 63 21 7 1 3 3 3 3 7

Продолжим усложнять наши примеры – возьмем четырехзначное число.

Решение

Как определить количество делителей конкретного числа

Решение

Раскладываем число на множители.

84 42 21 7 1 2 2 3 7

Ответ: всего у 84 будет 24 делителя – 12 положительных и 12 отрицательных.

Как вычислить общие делители нескольких чисел

Зная свойства наибольшего общего делителя, можно утверждать, что количество делителей некоторого набора целых чисел будет совпадать с количеством делителей НОД тех же чисел. Это будет справедливо не только для двух чисел, но и для большего их количества. Следовательно, чтобы вычислить все общие делители нескольких чисел, надо определить их наибольший общий множитель и найти все его делители.

Разберем пару таких задач.

Решение

Для этого нам потребуется алгоритм Евклида:

Решение

Чтобы узнать количество этих чисел, нужно выяснить, сколько положительных делителей имеет НОД.

Ответ: у данных чисел шесть общих делителей.

Источник

Нахождение всех делителей числа, число делителей числа

В данной статье мы поговорим о том, как найти все делители числа. Начнем с доказательства теоремы, с помощью которой можно задать вид всех делителей определенного числа. Далее возьмем примеры нахождения всех нужных делителей и покажем, как именно определить, сколько делителей имеет конкретное число. В последнем пункте подробно рассмотрим примеры задач на нахождение общих делителей нескольких чисел.

Как найти все делители числа

Сложнее определить все делители составного числа. Сформулируем теорему, которая лежит в основе данного действия.

Учитывая доказательство этой теоремы, мы можем сформировать схему нахождения всех положительных делителей данного числа.

Для этого нужно выполнить следующие действия:

Самым трудным в таком расчете является именно перебор всех комбинаций указанных значений. Разберем подробно решения нескольких задач, чтобы наглядно показать применение данной схемы на практике.

Решение

Для нахождения делителей удобно все полученные значения оформлять в виде таблицы:

Возьмем пример чуть сложнее: в нем при разложении числа получится не один, а два множителя.

Решение

Начнем с разложения данного числа на простые множители.

567 189 63 21 7 1 3 3 3 3 7

Продолжим усложнять наши примеры – возьмем четырехзначное число.

Решение

Как определить количество делителей конкретного числа

Решение

Раскладываем число на множители.

84 42 21 7 1 2 2 3 7

Ответ: всего у 84 будет 24 делителя – 12 положительных и 12 отрицательных.

Как вычислить общие делители нескольких чисел

Зная свойства наибольшего общего делителя, можно утверждать, что количество делителей некоторого набора целых чисел будет совпадать с количеством делителей НОД тех же чисел. Это будет справедливо не только для двух чисел, но и для большего их количества. Следовательно, чтобы вычислить все общие делители нескольких чисел, надо определить их наибольший общий множитель и найти все его делители.

Разберем пару таких задач.

Решение

Для этого нам потребуется алгоритм Евклида:

Решение

Чтобы узнать количество этих чисел, нужно выяснить, сколько положительных делителей имеет НОД.

Ответ: у данных чисел шесть общих делителей.

Источник

Простые числа. Составные числа

Определение 1. Простое число − это натуральное число больше единицы, которое делится только на себя и на 1.

Другими словами число является простым, если имеет только два различных натуральных делителя.

Определение 2. Любое натуральное число, которое кроме самого себя и единицы имеет и других делителей, называется составным числом.

Другими словами натуральные числа, не являющиеся простыми числами, называются составными. Из определения 1 следует, что составное число имеет больше двух натуральных делителей. Число 1 не является ни простым, ни составным т.к. имеет только один делитель 1 и, кроме этого многие теоремы относительно простых чисел не имеют места для единицы.

Из определений 1 и 2 следует, что каждое целое положительное число больше 1 является либо простым, либо составным числом.

Ниже представлена программа для отображения простых чисел до 5000. Заполните ячейки, нажмите на кнопку «Создать» и подождите несколько секунд.

Таблица простых чисел

Теорема 1. Любое составное число всегда может быть представлено и притом единственным способом в виде произведения конечного числа простых чисел.

Если k₁ число простое, то k уже представлен в виде произведения простых чисел, в противном случае существует такое простое число p₂, что

Если k₂ число составное, то мы продолжаем процедуру до тех пор, пока k не будет представлено в виде произведения простых чисел:

Первая часть теоремы доказана. Покажем, далее, что разложение составного числа на простые множители единственно (естественно, порядок множителей в произведении может быть другим).

Допустим существует два разложения числа k:

Так как k=p₁p₂p₃. делится на простое число q₁, то по крайней мере один из множителей, например p₁ делится на q₁. Но p₁ простое число и делится только на 1 и на себя. Следовательно p₁=q₁ (т.к. q₁≠1)

Таким образом убеждаемся, что всякое простое число входящее множителем в первое разложение один или несколько раз, входит и во второе разложение минимум столько же раз и наоборот, всякое простое число, которое входит множителем во второе разложение один или несколько раз входит и в первое разложение минимум столько же раз. Следовательно любое простое число входит множителем в оба разложения одинаковое число раз и, таким образом, эти два разложения одинаковы.■

Разложение составного числа k можно записать в следующем виде

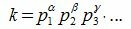(3)

Разложение (3) называется каноническим разложением числа.

Теорема 2. Количество простых чисел бесконечно много.

Доказательство. Предположим, что существует конечное число простых чисел, и пусть наибольшее простое число равно p. Рассмотрим все числа больше p. По предположению утверждения эти числа должны быть составными и должны делится по крайней мере на один из простых чисел. Выберем число, являющиеся произведением всех этих простых чисел плюс 1:

Число z больше p так как 2p уже больше p. p не делится ни на одно из этих простых чисел, т.к. при делении на каждое из них дает остаток 1. Таким образом мы приходим к противоречию. Следовательно существует бесчисленное множество простых чисел.

Данная теорема является частным случаем более общей теоремы:

Теорема 3. Пусть задана арифметическая прогрессия

где d разность арифметической прогрессии, m первый член, и пусть d и m взаимно простые числа. Тогда арифметическая прогрессия (5) содержит бесконечное множество простых чисел.

Нетрудно заметить, что при m=1 и d=1 мы получим теорему 2.

Число и сумма всех делителей числа

Теорема 1 дает возможность определить, делится число m на n, если эти числа разложены на простые множители.

Если m делится на n, то n является кратным m:

Тогда любое простое число, входящее в n, должно входить и в m, поэтому в n не могут входить другие простые множители, которые не входят в m и притом эти простые множители в n входят не более число раз, чем в m.

Справедливо и обратное. Если каждый простой множитель числа n входит по крайней мере столько же раз в число m, то m делится на n.

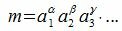Тогда все делители n числа m можно представить формулой

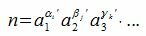(6)

Каждая из чисел n вычисленная формулой (6) является делителем числа m.

Очевидно, при разных значениях i, j, k имеем разные делители числа m. Тогда число всех делителей m равно:

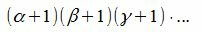Мы доказали следующую теорему:

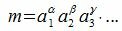каноническое разложение числа m. Тогда число делителей числа m равно:

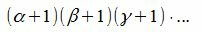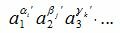
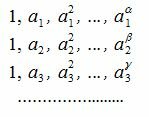Составим все произведения вида , которые различны между собой и являются множеством всех делителей числа m. Найдем сумму этих делителей. Для этого запишем ряды чисел

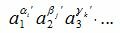
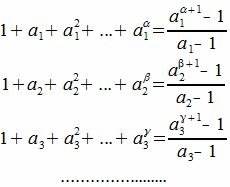Тогда для произведения вида берем по одному множителю из каждого горизонтального ряда. Используя правила умножения многочленов получим:

Заметим, что правая часть каждой строки является суммой членов геометрической прогрессии.

Следовательно сумма всех делителей числа m равна

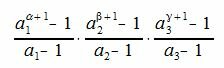(7)

Мы доказали следующую теорему:

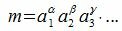каноническое разложение числа m. Тогда сумма всех делителей числа m равна выражению (7).

Источник