На что делится 509
На что делится 509
Вы думаете, что знаете все о числе 509? Здесь вы можете проверить свои знания об этом числе и выяснить, верны ли они, или вам еще есть что узнать о числе 509. Не знаете, чем может быть полезно знание характеристик числа 509? Подумайте, сколько раз вы используете числа в своей повседневной жизни, наверняка их больше, чем вы думали. Узнав больше о числе 509, вы сможете воспользоваться всем тем, что это число может вам предложить.
Описание числа 509
как написать 509 буквами?
Число 509 на английском языке записывается как.пятьсот девять
Число 509 произносится цифра за цифрой как (5) пять (0) ноль (9) девять.
Каковы делители числа 509?
У числа 509 есть 2 делителей, они следующие:
Является ли 509 простым числом?
Какие простые факторы 509?
Факторизация на простые множители 509 такова:
Что такое квадратный корень из 509?
Что такое квадрат из 509?
Квадрат из 509, результат умножения 509*509 это 259081
Как перевести 509 в двоичные числа?
Перевести десятичное число 509 в двоичные числа можно следующим образом.111111101
Как перевести 509 в восьмеричное число?
Как перевести 509 в шестнадцатеричную систему счисления?
Десятичное число 509 в шестнадцатеричной системе счисления имеет вид.1fd
Что такое натуральный или неперианский логарифм от 509?
Неперианский или натуральный логарифм числа 509 равен6.2324480165505
Что такое логарифм по основанию 10 от 509?
По основанию 10 логарифм 509 равен2.7067177823368
Каковы тригонометрические свойства числа 509?
Что такое синус 509?
Синус 509 радиан равен0.061950423737128
Что такое косинус 509?
Косинус 509 радиан равен 0.9980792278165
Что такое тангенс 509?
Тангенс 509 радиан равен0.062069645385424
Информация о числах
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел.
Сейчас изучают числа:
Число 509
Пятьсот девять
RGB(0, 1, 253) или #0001FD
(возможное основание)
свобода, движение, разнообразие, приключения, путешествия, риск, опасность, страх
Описание числа 509
Представления числа: двоичная система: 111111101, троичная система: 200212, восьмеричная система: 775, шестнадцатеричная система: 1FD. 509 байтов представляет из себя число байт 509.
Косинус числа: 0.9981, синус числа: 0.0620, тангенс числа: 0.0621. Натуральный логарифм числа 509: 6.2324. Логарифм десятичный числа 509: 2.7067. 22.5610 — корень квадратный из числа 509, 7.9843 — кубический корень. Возведение числа 509 в квадрат: 2.5908e+5.
Признаки делимости чисел
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Что такое «признак делимости»
Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.
Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.
Однозначные, двузначные и трехзначные числа
Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.
Трехзначные числа — числа, в составе которых три знака (три цифры).
Чётные и нечётные числа
Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!
Признаки делимости чисел
Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.
Признак делимости на 3. Сумма цифр числа должна делиться на 3.
Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.
Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.
Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.
Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.
Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.
Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.
Простые числа в математике
Что такое простые числа
Простые числа — натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Другими словами, число x является простым, если оно больше 1 и при этом делится без остатка только на 1 и на x.
Например, 11 — это простое число. Его можно разделить только на 1 и 11. Деление простого числа на другое приводит к тому, что остается остаток, что называют простым числом.
13 ÷ 4 = 3 (остаток 1).
Число, имеющее более двух множителей, называется составными числами. Наименьшее простое число равно 2, потому что оно делится само на себя и только на 1.
30 не является примером простого числа, потому что его можно разделить на 1,2,3,5,6,10,15,30. Таким образом, 30 является примером составного числа, поскольку оно имеет более двух факторов.
Ноль, единица и числа меньше единицы не считаются простыми числами.
Основная теорема арифметики, лемма Евклида
Основная идея теоремы арифметики — это любое целое число больше 1 либо является простым числом, либо может быть получено путем умножения простых чисел вместе.
Фундаментальная теорема арифметики (название которой указывает на ее основную важность) гласит, что любое число может быть учтено в уникальном списке простых чисел.
Простое число (2,3,5,7,11. ) против составного (4=2×2, 6=2×3, 8=2x2x2, 12=2x2x3. ).
Этот ряд примеров можно продолжить:
Таким образом, они либо простые, либо простые числа, умноженные друг на друга.
Число 42. Можем ли мы получить 42, умножив только простые числа?
Да, 2, 3 и 7 являются простыми числами, и при умножении вместе они составляют 42.
Число 7. 7 уже является простым числом
Число 22. 22 может быть получено путем умножения простых чисел 2 и 11 вместе.
Никакая другая комбинация простых чисел не будет работать.
Лемма — это, как правило, незначительное, доказанное утверждение, которое используется в качестве ступеньки к доказательству более сложной математической теории. По этой причине она также известна как «вспомогательная теорема».
В теории чисел лемма Евклида — это лемма, которая отражает фундаментальное свойство простых чисел, а именно: если простое число p делит произведение ab двух целых чисел a и b, то p должно разделить, по крайней мере, одно из этих целых чисел a и b.
Если p = 19, a = 133, b = 143, то ab = 133 × 143 = 19019, и поскольку это делится на 19, лемма подразумевает, что один или оба из 133 или 143 также должны быть. На самом деле 133 = 19 × 7.
Если предпосылка леммы не выполняется, т. е. p является составным числом, его следствие может быть либо истинным, либо ложным.
В случае p = 10, a = 4, b = 15 составное число 10 делит ab = 4 × 15 = 60, но 10 не делит ни 4, ни 15.
Это свойство является ключевым в доказательстве фундаментальной теоремы арифметики. Лемма Евклида показывает, что в целых числах неприводимые элементы также являются простыми элементами.
Таким образом, изучение чисел в основном сводится к изучению свойств простых чисел. Математики на протяжении тысячелетий довольно много выяснили о простых числах. Одно из самых известных доказательств Евклида показывает, что существует бесконечно много простых чисел.
Как определить простые числа
Сначала попробуйте разделить его на 2 и посмотреть, получится ли целое число. Если да, то оно не может быть простым числом. Если вы не получите целое число, затем попробуйте разделить его на простые числа: 3, 5, 7, 11 (9 делится на 3) и так далее, всегда делясь на простое число.
8 простых чисел до 20: 2, 3, 5, 7, 11, 13, 17 и 19.
Первые 10 простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Таблица простых чисел до 1000:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 |
| 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 |
| 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 |
| 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 |
| 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 |
| 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 |
| 349 | 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 |
| 409 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 |
| 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 |
| 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 |
| 659 | 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 |
| 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 |
| 809 | 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 |
| 863 | 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 |
| 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
2 — наименьшее простое число. Это также единственное четное простое число — все остальные четные числа могут быть разделены сами по себе на 1 и 2, что означает, что у них будет, по крайней мере, 3 фактора.
Один из самых известных математиков классической эпохи, Евклид, записал доказательство того, что не существует самого большого простого числа. Самое большое известное простое число (по состоянию на ноябрь 2020 года) составляет 282 589 933-1, число, которое имеет 24 862 048 цифр при записи в базе 10. До этого самым большим известным простым числом было 277 232 917-1, состоящее из 23 249 425 цифр.
За исключением 2 и 3, все остальные простые числа могут быть выражены в общей форме как 6n + 1 или 6n — 1, где n — натуральное число.
Чтобы определить, является ли число простым или составным, нужно решить пример на делимость в следующем порядке (от простого к сложному): 2, 5, 3, 11, 7, и 13. Если вы обнаружите, что число делится на одно из них, и вы знаете, что оно составное, не нужно выполнять остальные тесты.
Если число меньше 121 не делится на 2, 3, 5 или 7, оно простое; в противном случае оно составное.
Если число меньше 289 не делится на 2, 3, 5, 7, 11, или 13, это простое число; в противном случае оно составное.
Примеры решения задач
Является ли 19 простым числом или нет?
Как понять, что число простое можно двумя способами.
Формула для простого числа равна 6n + 1
Запишем данное число в виде 6n + 1.
Проверьте на наличие факторов 19
Следовательно, с помощью обоих методов докажем, что 19 имеет только два фактора 1 и 19, что означает простое число.
53 — это простое число или нет?
Как доказать, что число простое, используя приведенную ниже формулу. Чтобы узнать простые числа, превышающие 40, можно:
32 + 3 + 41 = 9 + 3 + 41 = 53
53 имеет только факторы 1 и 53.
Итак, 53 является простым числом по обоим методам.
Является ли число простым или составным?
Число 185 заканчивается на 5, поэтому оно делится на 5. Оно составное.
Как проверить простое ли число 243?
Число 243 заканчивается нечетным числом, поэтому оно не делится на 2. Он не заканчивается на 5 или 0, поэтому он не делится на 5. Его цифровой корень равен 9 (потому что 2 + 4 + 3 = 9), так что оно делится на 3.
Мерзляк 5 класс — § 18. Деление
Вопросы к параграфу
1.Что значит разделить число а на число b?
Разделить число а на число b — это значит найти такое число, которое при умножении на число b даёт число b.
2. Как в равенстве а : b = с называют число а? Число b? Число с? Выражение а : b?
3. Что показывает частное двух чисел?
Частное число двух чисел а и b показывает во сколько раз делитель b меньше делимого а.
4. На какое число делить нельзя?
Нельзя делить на число 0.
5. Чему равно частное отделения числа 0 на любое натуральное число?
Частное отделения числа 0 на любое натуральное число равно нулю: 0 : а = 0.
6. Чему равно частное а : а, где а ≠ 0? а : 1?
7. Как найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
8. Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
9. Как найти неизвестный делитель?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решаем устно
1. Заполните цепочку вычислений:
2. Выполните деление:
3. Укажите среди данных произведений наибольшее:
4. Догоняя Сашу, Слава бежит со скоростью 180 м/мин. Чему равна скорость Саши, если мальчики сближаются со скоростью 12 м/мин?
Если мальчики во время бега в одну сторону сближаются, значит скорость Славы больше, чем скорость Саши.
По условию, скорость сближения составляет 12м/мин, то есть Саша бежит медленнее Славы на 12м/мин:
180 — 12 = 168 (м/мин) — скорость Саши.
5. Два автомобиля двигаются навстречу друг другу, причём один из них со скоростью 74 км/ч. Чему равна скорость второго автомобиля, если они сближаются со скоростью 150 км/ч?
Если автомобили двигаются навстречу друг другу, то их скорость сближения равна сумме скорости первого автомобиля и скорости второго автомобиля:
v (сближения) = v (первого автомобиля) + v (второго автомобиля).
v (второго автомобиля) = v (сближения) — v (первого автомобиля)
150 — 74 = 76 (км/ч) — скорость второго автомобиля.
Упражнения
447. Известно, что 243 • 425 = 103 275. Чему равно значение выражения:
448. Известно, что 4 608 : 48 = 96. Чему равно значение выражения:
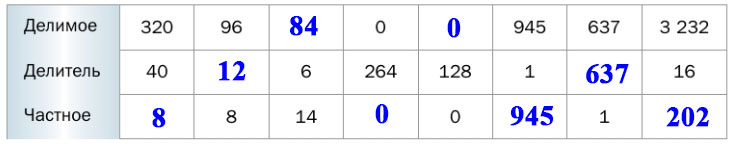
449. Заполните таблицу.
450. Выполните деление:
451. Выполните деление:
452. Выполните деление:
453. Выполните деление:
454. Выполните действия:
455. Найдите значение выражения:
456. Найдите значение выражения:
457. Решите уравнение:
458. Решите уравнение:
459. Всадник преодолевает расстояние между двумя сёлами за 5 ч, если двигается со скоростью 12 км/ч. С какой скоростью он должен двигаться, чтобы преодолеть это расстояние за 4 ч?
1) 12 • 5 = 60 (км) — расстояние между двумя сёлами.
2) 60 : 4 = 15 (км/ч) — скорость всадника для того, чтобы преодолеть 60 км за 4 часа.
460. Вика купила 8 кг конфет по 630 р. за килограмм. Сколько килограммов конфет по 420 р. за килограмм она сможет купить за эти же деньги?
1) 630 • 8 = 5 040 (рублей) — стоимость покупки.
2) 5 040 : 420 = 12 (кг) — конфет можно купить за эти же деньги.
461. Найдите значение выражения:
462. Найдите значение выражения:
463. Малыш купил для Карлсона 8 пирожных и 12 булочек с повидлом, заплатив за всю покупку 408 крон. Одно пирожное стоит 24 кроны. Какова цена одной булочки?
1) 24 • 8 = 192 (кроны) — стоили пирожные.
2) 408 — 192 = 216 (крон) — стоили булочки.
3) 216 : 12 = 18 (крон) — цена одной булочки.
464. Дед Афанасий заготовил на зиму 6 бочек квашеной капусты и 14 бочонков солёных огурцов. В одной бочке вмещается 26 кг капусты. Сколько килограммов огурцов в одном бочонке, если всего дед Афанасий заготовил 324 кг овощей?
2) 324 — 156 = 168 (кг) — заготовлено огурцов.
3) 168 : 14 = 12 (кг) — вместимость одной бочки с огурцами.
465. Сколько килограммов масла можно изготовить из 261 кг сливок, если из 9 кг сливок получается 2 кг масла?
1) 261 : 9 = 29 (раз) — больше сливок будет использовано для изготовления масла.
2) 2 • 29 = 58 (кг) — масла получится из 261 кг сливок.
466. Автомобиль расходует 8 л бензина на 100 км пути. Хватит ли 20 л бензина, чтобы доехать из Рязани до Владимира, расстояние между которыми по трассе равно 248 км?
1) Так как 20 л = 8 л + 8 л + 4 л (ровно половина от 8 л), то 20 литров бензина хватит, чтобы проехать 100 км + 100 км + 50 км (половину от 100 км) = 250 км.
2) 250 км > 248 км, значит 20 литров бензина хватит, чтобы доехать по трассе из Рязани до Владимира.
467. Было собрано 328 кг проса. Сколько из этого проса можно получить пшена, если из 4 кг проса получается 3 кг пшена?
1) 328 : 4 = 82 (раза) — больше проса собрали.
2) 82 • 3 = 246 (кг) — пшена можно изготовить из 328 кг проса.
468. Расстояние между двумя пристанями равно 476 км. Двигаясь по течению реки, катер проходит это расстояние за 14 ч. За сколько часов он пройдёт это расстояние против течения реки, если скорость течения равна 3 км/ч?
1) 476 : 14 = 34 (км/ч) — скорость катера по течению реки.
2) 34 — 3 = 31 (км/ч) — собственная скорость катера.
3) 31 — 3 = 28 (км/ч) скорость катера против течения реки.
4) 476 : 28 = 17 (часов) — потребуется катеру для прохождения 476 км против течения реки.
469. Расстояние между двумя портами равно 504 км. Двигаясь против течения реки, теплоход проходит это расстояние за 21 ч. За сколько часов он пройдёт это расстояние по течению реки, если скорость течения равна 2 км/ч?
1) 504 : 21 = 24 (км/ч) — скорость теплохода против течения реки.
2) 24 + 2 = 26 (км/ч) — собственная скорость теплохода.
3) 26 + 2 = 28 (км/ч) — скорость теплохода по течению реки.
4) 504: 28 = 18 (ч) — потребуется теплоходу для прохождения 504 км по течению реки.
470. Из городов Цветочный и Солнечный, расстояние между которыми равно 136 км, выехали одновременно навстречу друг другу Винтик и Шпунтик. Винтик двигался со скоростью 16 км/ч. С какой скоростью ехал Шпунтик, если они встретились через 4 ч после выезда?
1) 16 • 4 = 64 (км) — проехал до встречи Винтик.
2) 136 — 64 = 72 (км) — проехал до встречи Шпунтик.
3) 74 : 4 = 18 (км/ч) — скорость Шпунтика.
471. Расстояние между двумя городами равно 1 264 мили (1 сухопутная миля = 1 609 м). Из них одновременно вылетели навстречу друг другу два вертолёта и встретились через 8 ч после вылета. Скорость одного из вертолётов 82 миль/ч. С какой скоростью летел второй вертолёт?
1) 82 • 8 = 656 (миль/ч) — пролетел до встречи первый вертолёт.
2) 1 264 — 656 = 608 (миль) — пролетел до встречи второй вертолёт.
3) 608 : 8 = 76 (миль/ч) — скорость второго вертолёта.
472. В 6 ч утра из Мурома в Киев выехал со скоростью 9 км/ч Илья Муромец. В 8 ч утра из Мурома в Киев выехал Алёша Попович и догнал Илью Муромца в 2 ч дня. С какой скоростью ехал Алёша Попович?
2 часа дня = 14 часов
1) 14 — 6 = 8 (часов) — ехал до места встречи Илья Муромец.
2) 9 • 8 = 72 (км) — проехал до места встречи Илья Муромец.
3) 14 — 8 = 6 (часов) — ехал до места встречи Алёша Попович.
4) 72 : 6 = 12 (км/ч) — скорость Алёши Поповича.
473. В 8 ч 57 мин черепаха Катрина отправилась в путешествие из своего пруда в соседний. В 9 ч 5 мин из этого же пруда в том же направлении отправилась черепаха Виктория и догнала Катрину в 9 ч 29 мин. Найдите, с какой скоростью двигалась Катрина, если известно, что Виктория двигалась со скоростью 8 м/мин.
1) 9 ч 29 мин — 9 ч 5 мин = 24 (минуты) — двигалась до встречи черепаха Виктория.
2) 8 • 24 = 192 (метра) — проползла черепаха Виктория до места встречи.
3) 9 ч 29 мин — 8 ч 57 мин = 8 ч 89 мин — 8 ч 57 мин = 32 (минуты) — двигалась до встречи черепаха Катрин.
4) 192 : 32 = 6 (м/мин) — скорость черепахи Катрин.
474. С двух станций, расстояние между которыми равно 24 км, одновременно в одном направлении отправились два поезда. Впереди двигался поезд со скоростью 58 км/ч. Через 4 ч после начала движения его догнал второй поезд. Найдите скорость второго поезда.
1) 58 • 4 = 232 (км) — проехал первый поезд до места встречи.
2) 232 + 24 = 256 (км) — проехал второй поезд до места встречи.
3) 256 : 4 = 64 (км/ч) — скорость второго поезда.
475. Расстояние между сёлами Грушевое и Яблоневое равно 30 км. Из этих сёл одновременно в одном направлении отправились казаки Серошапка и Черноус. Черноус скакал на коне со скоростью 9 км/ч и через 6 ч после начала движения догнал Серошапку, который шёл пешком. С какой скоростью шёл Серошапка?
1) 9 • 6 = 54 (км) — проехал Черноус до места встречи.
2) 54 — 30 = 24 (км) — прошёл Серошапка до места встречи.
3) 24 : 6 = 4 (км/ч) — скорость Серошапки.
476. Расстояние между городками Сен-Жермен и Сен-Антуан равно 12 лье (старинная французская единица длины, 1 лье приблизительно равно 4 444 м). Из этих городков одновременно в одном направлении выехали Портос со скоростью 1 лье/ч и д’Артаньян со скоростью 3 лье/ч, причём Портос скакал впереди. Через сколько часов после выезда д’Артаньян догонит Портоса?
1) 3 — 1 = 2 (лье/ч) — скорость сближения Портоса и д’Артаньяна.
Это значит, что за 1 час д’Артаньян проедет столько же лье, что и Портос (1 лье) и дополнительно ещё 2 лье.
Так как расстояние между точками отправления Портоса и д’Артаньяна равно 12 лье, то д’Артаньян должен преодолеть тоже самое расстояние, что и Портос, и плюс ещё 12 км. Найдем сколько времени потребуется на преодоление 12 км со скоростью сближения:
2) 12 : 2 = 6 (часов) — надо, чтобы д’Артаньян догнал Портоса.
Комментарий: Проверим правильность наших рассуждений:
Значит наши рассуждения были правильными.
477. Расстояние между островами Акулий и Китовый равно 48 морским милям (1 морская миля = 1 852 м). От этих островов одновременно в одном направлении отчалили фрегаты «Отважный» и «Стремительный», причём «Отважный» плыл впереди «Стремительного». Скорость «Отважного» равна 12 миль/ч, а «Стремительного» — 18 миль/ч. Через сколько часов «Стремительный» догонит фрегат «Отважный»?
1) 18 — 12 = 6 (миль/час) — скорость сближения фрегатов «Отважный» и «Стремительный».
2) 48 : 6 = 8 (ч) — потребуется «Стремительному», чтобы догнать «Отважный».
478. Школьники Василий, Андрей, Дмитрий и Сергей собрали 326 кг яблок. Василий собрал 37 кг яблок, что в 3 раза меньше, чем Андрей, а Дмитрий и Сергей собрали яблок поровну. Кто из школьников собрал больше килограммов яблок?
1) 37 • 3 = 111 (кг) — яблок собрал Андрей.
2) 37 + 111 = 148 (кг) — яблок собрали Василий и Андрей вместе.
3) 326 — 148 = 178 (кг) — яблок собрали Дмитрий и Сергей вместе.
4) 178 : 2 = 89 (кг) — яблок каждый собрал Дмитрий и Сергей.
5) 111 кг (Андрей) > 89 кг (Дмитрий или Сергей) > 37 кг (Василий).
Ответ: больше всего килограммов яблок собрал Андрей.
479. Рабочие Иван, Пётр, Степан и Павел изготовили 160 деталей. Иван изготовил 81 деталь, что в 3 раза больше, чем изготовил Пётр, а Степан и Павел изготовили деталей поровну. Кто из рабочих изготовил меньше всех деталей?
1) 81 : 3 = 27 (шт) — деталей изготовил Петр.
2) 81 + 27 = 108 (шт) — деталей изготовили Иван и Петр вместе.
3) 160 — 108 = 52 (шт) — деталей изготовили Степан и Павел вместе.
4) 52 : 2 = 26 (шт) — деталей каждый изготовили Степан и Павел.
5) 26 шт. (Степан или Павел)
Ответ: меньше всех деталей изготовили Степан и Павел — по 26 штук деталей каждый.
480. Буратино живёт на расстоянии 1 км 200 м от школы. Уроки в школе начинаются в 8 ч 30 мин. Буратино делает за минуту 120 шагов, длина шага — 40 см. В котором часу Буратино должен выходить из дома, чтобы приходить в школу за 10 мин до начала занятий?
1 км 200 м = 1 200 метров = 120 000 см
1) 120 000 : 40 = 3 000 (шагов) — должен сделать Буратино, чтобы дойти до школы.
2) 3 000 : 120 = 25 (минут) — нужно Буратино, чтобы дойти до школы.
3) 8 ч 30 мин — 10 мин — 25 мин = 8 ч 20 мин — 25 мин = 7 ч 80 мин — 25 мин = 7 ч 55 мин — время выхода Буратино из дома.
Ответ: Буратино должен выйти из дома в 7 ч 55 мин.
481. Дежурные первого отряда за 6 мин чистят 24 картофелины, а дежурные второго отряда за 9 мин — 45 картофелин. За сколько минут совместной работы они почистят 198 картофелин?
1) 24 : 6 = 4 (шт/мин) — производительность чистки картофеля 1 отряда.
2) 45 : 9 = 5 (шт/мин) — производительность чистки картофеля 2 отряда.
3) 4 + 5 = 9 (шт/мин) — совместная производительность чистки картофеля.
4) 198 : 9 = 22 (мин) — потребуется 1 и 2 отряду совместно для чистки 198 картофелин.
482. На сколько дней школьной столовой хватит 800 л сока, если мальчики за 8 дней выпивают 960 л сока, а девочки за 6 дней — 480 л?
1) 960 : 8 = 120 (л/день) — скорость, с которой пьют сок мальчики.
2) 480 : 6 = 80 (л/день) — скорость, с которой пьют сок девочки.
3) 120 + 80 = 200 (л/день) — совместная скорость, с которой пьют сок мальчики и девочки.
4) 800 : 200 = 4 (дня) — на столько дней хватит сока в школьной столовой.
483. За четыре дня работы три оператора набрали на компьютере вместе 288 страниц. Сколько страниц наберёт один оператор за 7 дней, если у них одинаковая производительность труда?
1) 288 : 4 = 72 (страницы/день) — производительность трёх операторов.
2) 72 : 3 = 24 (страницы/день) — производительность одного оператора.
3) 24 • 7 = 168 (страниц) — наберёт один оператор за 7 дней.
484. Для работы шести одинаковых двигателей в течение 8 ч требуется 672 л топлива. На сколько часов работы хватит 98 л топлива одному такому двигателю?
1) 672 : 8 = 84 (л/час) — расход топлива для шести двигателей.
2) 84 : 6 = 14 (л/час) — расход топлива для одного двигателя.
3) 98 : 14 = 7 (часов) — время работы одного двигателя на 98 литрах топлива.
485. Белочки Рыженькая и Жёлтенькая собирали орехи. Рыженькая собрала 6 мешочков орехов, а Жёлтенькая — 7 таких же мешочков. Вместе они собрали 52 кг орехов. Сколько килограммов орехов собрала Рыженькая и сколько — Жёлтенькая?
1) 6 + 7 = 13 (шт) — мешков собрали белочки совместно.
2) 52 : 13 = 4 (кг) — объем одного мешка с орехами.
3) 6 • 4 = 24 (кг) — собрала Рыженькая.
4) 7 • 4 = 28 (кг) — собрала Жёлтенькая.
Ответ: Рыженькая собрала 24 кг орехов, а Жёлтенькая — 28 кг орехов.
486. Двигаясь по пустыне в течение трёх дней, караван преодолел 63 км. В первый день караван двигался 6 ч, во второй — 8 ч, а в третий — 7 ч. Сколько километров проходил караван каждый день, если известно, что он двигался все дни с постоянной скоростью?
1) 6 + 8 + 7 = 21 (час) — всего двигался караван за три дня.
2) 63 : 21 = 3 (км/час) — скорость движения каравана.
4) 3 • 8 = 24 (км) — прошёл караван во 2 день.
5) 3 • 7 = 21 (км) — прошёл караван в 3 день.
Ответ: в 1 день — 18 км, во 2 день — 24 км, в 3 день — 21 км.
487. Фермер привёз на рынок 420 кг яблок и 180 кг груш в 50 ящиках. Сколько ящиков было с яблоками и сколько — с грушами, если известно, что массы всех ящиков равны?
1) 420 + 180 = 600 (кг) — привезли фруктов всего.
2) 600 : 50 = 12 (кг) — масса одного ящика.
3) 420 : 12 = 35 (шт) — ящики с яблоками.
4) 180 : 12 = 15 (шт) — ящики с грушами.
Ответ: Привезли 35 шт ящиков с яблоками и 15 шт ящиков с грушами.
488. Али-Баба перевозил найденное в пещере разбойников золото на четырёх ослах в 22 одинаковых мешках. На первого осла он погрузил 80 кг золота, на второго — 100 кг, на третьего — 120 кг, на четвёртого — 140 кг. Сколько мешков золота было нагружено на каждого осла?
1) 80 + 100 + 120 + 140 = 440 (кг) — объем золота всего.
2) 440 : 22 = 20 (кг) — масса одного мешка с золотом.
3) 80 : 20 = 4 (мешка) — погрузили на 1 осла.
3) 100 : 20 = 5 (мешков) — погрузили на 2 осла.
3) 120 : 20 = 6 (мешков) — погрузили на 3 осла.
3) 140 : 20 = 7 (мешков) — погрузили на 4 осла.
Ответ: на первого осла погрузили 4 мешка, на второго — 5 мешков, на третьего — 6 мешков, на четвёртого осла погрузили 7 мешков золота.
489. Решите уравнение:
490. Решите уравнение:
491. Решите уравнение:
492. Решите уравнение:
493. Решите уравнение:
494. Решите уравнение:
495. Отец с сыном посадили 108 кустов помидоров, причём отец посадил в 2 раза больше, чем сын. Сколько кустов помидоров посадил сын?
Так как отец посадил в 2 раза больше кустов помидор, чем сын, то можно сказать, что сын посадил 1 часть кустов, а отец 2 части кустов помидор:
1) 1 часть + 2 части = 3 части — составляют общее количество посаженных кустов помидор.
2) 108 : 3 = 36 (шт) — кустов помидор составляет одна часть от общего количества посаженного.
3) 36 • 1 = 36 (шт) — кустов помидор посадил сын.
Ответ: сын посадил 36 шт кустов помидор.
496. В два магазина завезли 268 кг шампиньонов, причём в первый магазин завезли шампиньонов в 3 раза меньше, чем во второй. Сколько килограммов шампиньонов завезли в каждый магазин?
Так как в первый магазин завезли шампиньонов в 3 раза меньше, чем во второй, то можно сказать, что в первый магазин завезли 1 часть шампиньонов, а во второй — 3 части:
1) 1 часть + 3 части = 4 части — составляют общее количество шампиньонов.
2) 268 : 4 = 67 (кг) — шампиньонов составляет одна часть всего завезённого товара.
3) 67 • 1 = 67 (кг) — шампиньонов завезли в первый магазин.
4) 67 • 3 = 201 (кг) — шампиньонов завезли во второй магазин.
Ответ: в первый магазин — 67 кг, а во второй магазин — 201 кг.
497. В двух залах кинотеатра демонстрировались два кинофильма. В первом зале зрителей было в 7 раз больше, чем во втором. Сколько зрителей находилось во втором зале, если известно, что их было на 156 меньше, чем в первом?
1) 7 частей — 1 часть = 6 частей — разница между количеством зрителей в первом и во втором зале.
2) 156 : 6 = 26 (человек) — составляет одна чать от общего количества зрителей в обоих залах.
3) 26 • 1 = 26 (человек) — количество зрителей в первом зале.
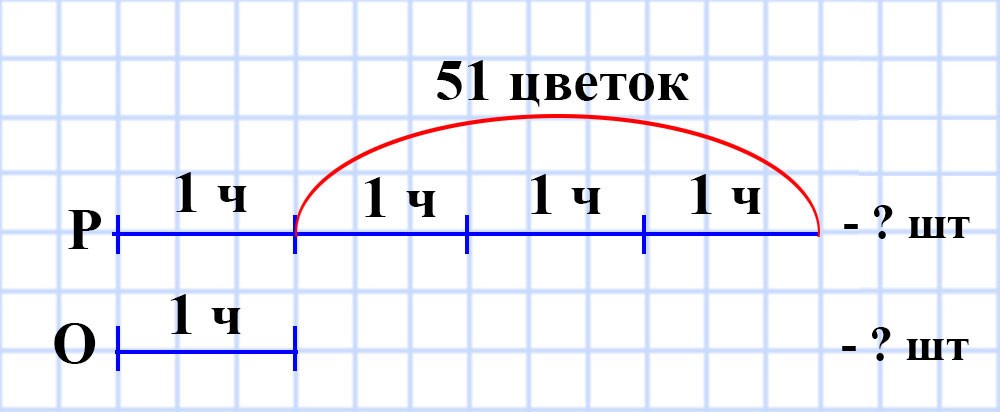
498. Валентин подарил Виктории розы и орхидеи, причём орхидей было в 4 раза меньше, чем роз. Сколько роз подарил Валентин, если известно, что их было на 51 больше, чем орхидей?
1) 4 — 1 = 3 (части) — разница между количеством роз и орхидей.
2) 51 : 3 = 17 (шт) — составляет 1 часть от общего количества.
3) 17 • 4 = 68 (шт) — количество подаренных роз.
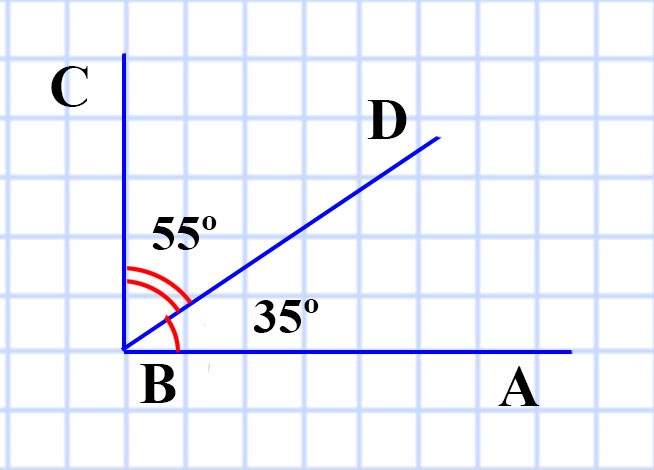
499. Из вершины прямого угла проведён луч так, что он делит прямой угол на два угла, один из которых больше второго на 20°. Найдите величину каждого из образовавшихся углов.
1) 90º — 20º = 70º — была бы сумма углов ABD и DBC, если бы они были равны.
2) 70º : 2 = 35º — величина ∠ABD.
3) 35º + 20º = 55º — величина ∠DBC.
Ответ: ∠ABD = 35º, ∠DBC = 55º.
500. Из вершины развёрнутого угла проведён луч так, что он делит развёрнутый угол на два угла, один из которых меньше второго на 50º. Найдите величину каждого из образовавшихся углов.
∠ABC = 180º — развёрнутый.
1) 180º — 50º = 130º — была бы сумма углов ABD и DBC, если бы они были равны.
2) 130º : 2 = 65º — величина ∠DBC.
3) 65º + 50º = 115º — величина ∠ABD.
Ответ: ∠ABD = 115º, ∠DBC = 65º.
501. В три магазина завезли 264 кг яблок. В первый магазин завезли в 3 раза больше яблок, чем в третий, а во второй — в 2 раза больше, чем в третий. Сколько килограммов яблок завезли в каждый магазин?
1) 1 + 2 + 3 = 6 (частей) — общее количество частей, на которые можно разделить яблоки.
2) 264 : 6 = 44 (кг) — составляет одна часть от завезённых во все магазины яблок.
3) 44 • 3 = 132 (кг) — яблок завезли в первый магазин.
4) 44 • 2 = 88 (кг) — яблок завезли во второй магазин.
5) 44 • 1 = 44 (кг) — яблок завезли в третий магазин.
Ответ: в первый магазин — 132 кг, во второй магазин — 88 кг, в третий магазин — 44 кг.
502. За четыре дня путешествия капитан Врунгель проплыл 546 миль. Во второй день он проплыл в 4 раза больше, чем в первый, в третий — в 3 раза больше, чем в первый, а в четвёртый — в 5 раз больше, чем в первый. Сколько миль проплывал капитан Врунгель ежедневно?
1) 1 + 4 + 3 + 5 = 13 (частей) — общее количество частей, на которое можно разделить весь путь.
2) 546 : 13 = 42 (км) — составляет одна часть пути.
3) 42 • 1 = 42 (км) — проплыл Врунгель в первый день.
4) 42 • 4 = 168 (км) — проплыл Врунгель во второй день.
5) 42 • 3 = 126 (км) — проплыл Врунгель в третий день.
6) 42 • 5 = 210 (км) — проплыл Врунгель в четвёртый день.
Ответ: в первый день — 42 км, во второй день — 168 км, в третий день — 126 км, в четвёртый день — 210 км.
503. Егор, Саша и Алёша поймали 256 окуней. Егор поймал в 3 раза больше рыб, чем Саша, а Алёша — столько, сколько Егор и Саша вместе. Сколько окуней поймал лучший рыбак?
1) 1 + 3 = 4 (части) — от общего количества пойманной рыбы поймал Алёша.
2) 1 + 3 + 4 = 8 (частей) — количество частей, на которое можно разделить пойманную рыбу.
3) 256 : = 32 (шт) — окуней составляет одна часть пойманной рыбы.
4) 32 • 1 = 32 (шт) — окуней поймал Саша.
5) 32 • 3 = 96 (шт) — окуней поймал Егор.
6) 32 • 4 = 128 (шт) — окуней поймал Алёша.
7) 128 шт (Алёша) > 96 шт (Егор) > 32 шт (Саша).
Ответ: Лучшим рыбаком оказался Алёша. Он поймал 128 штук окуней.
504. Красная Шапочка, Мальвина, Золушка и Дюймовочка слепили 500 пельменей. Красная Шапочка слепила в 2 раза больше пельменей, чем Дюймовочка, Мальвина — столько, сколько Красная Шапочка и Дюймовочка вместе, а Золушка — столько, сколько Мальвина и Дюймовочка вместе. Сколько пельменей слепила каждая девочка?
1) 1 + 2 = 3 (части) — от общего числа пельменей слепила Мальвина.
2) 3 + 1 = 4 (части) — от общего числа пельменей слепила Золушка.
3) 1 + 2 + 3 + 4 = 10 (частей) — можно разделить все слепленные пельмени.
4) 500 : 10 = 50 (шт) — пельменей составляет одна часть.
5) 50 • 1 = 50 (шт) — пельменей слепила Дюймовочка.
6) 50 • 2 = 100 (шт) — пельменей слепила Красная Шапочка.
7) 50 • 3 = 150 (шт) — пельменей слепила Мальвина.
8) 50 • 4 = 200 (шт) — пельменей слепила Золушка.
Ответ: Дюймовочка — 50 шт, Красная Шапочка — 100 шт. Мальвина — 150 шт, Золушка — 200 шт.
505. В трёх вагонах электропоезда ехало 246 пассажиров. В первом вагоне было в 2 раза больше пассажиров, чем во втором, а в третьем — на 78 пассажиров больше, чем во втором. Сколько пассажиров ехало в каждом вагоне?
Пусть в во втором вагоне ехало х пассажиров, тогда в первом вагоне ехало 2х пассажиров, а в третьем вагоне — (х+78) пассажиров. Всего в трёх вагонах электропоезда ехало 246 пассажиров.
Можно составить уравнение:
2х + х + (х + 78) = 246
(2х + х + х) + 78 = 246
4х + 78 = 246
4х = 246 — 78
4х = 168
х = 168 : 4
х = 42 (пассажира) — ехало во втором вагоне.
Найдём количество пассажиров в других вагонах электропоезда:
2х = 2 • 42 = 84 (пассажира) — ехало в первом вагоне.
х + 78 = 42 + 78 = 120 (пассажиров) — ехало в третьем вагоне.
Ответ: в первом вагоне 84 пассажира, во втором вагоне — 42 пассажира, а в третьем вагоне — 120 пассажиров.
506. В три школы отправили 552 кг апельсинов, причём в одну школу отправили в 6 раз меньше апельсинов, чем во вторую, и на 136 кг меньше, чем в третью. Сколько килограммов апельсинов отправили в каждую школу?
Пусть х кг апельсинов отправили в первую школу. Тогда во вторую школу отправили 6х кг апельсинов, в а третью — (х+136) кг апельсинов. Всего в три школы отправили 552 кг апельсинов.
Можно составить уравнение:
х + 6 х + (х + 136) = 552
(х + 6х + х) +136 = 552
8х + 136 = 552
8х = 552-136
8х = 416
х = 416 : 8
х = 52 (кг) — апельсинов отправили в первую школу.
Найдём количество апельсинов отправленных в другие школы:
6х = 6 • 52 = 312 (кг) — апельсинов отправили во вторую школу.
х + 136 = 52 + 136 = 188 (кг) — апельсинов отправили в третью школу.
Ответ: в первую школу отправили 52 кг апельсинов, во вторую — 312 кг апельсинов, а в третью — 188 кг апельсинов.
507. Одна из сторон треугольника в 5 раз меньше второй и на 25 см меньше третьей. Найдите стороны треугольника, если его периметр равен 74 см.
Пусть первая сторона треугольника равна х см, тогда вторая сторона треугольника равна 5х см, а третья — (х + 25) см. Периметр треугольника равен 74 см.
Можем составить уравнение:
х + 5х + (х + 25) = 74
(х + 5х + х) + 25 = 74
7х + 25 = 74
7х = 74 — 25
7х = 49
х = 7 (см) — длина первой стороны треугольника.
Найдём длину остальных сторон треугольника:
5х = 5 • 7 = 35 (см) — длина второй стороны треугольника.
7 + 25 = 32 (см) — длина третьей стороны треугольника.
Ответ: длина первой стороны треугольника 7 см, второй стороны — 35 см, а третьей стороны — 32 см.
508. Одна из сторон треугольника в 2 раза больше второй стороны, а вторая — на 7 дм меньше третьей. Найдите стороны треугольника, если его периметр равен 99 дм.
Пусть длина второй стороны треугольника равна х дм, тогда длина первой стороны треугольника равна 2х дм, а третьей стороны — (х + 7) дм. Периметр треугольника равен 99 дм.
Можем составить уравнение:
2х + х + (х + 7) = 99
(2х + х + х) + 7 = 99
4х + 7 = 99
4х = 99 — 7
4х = 92
х = 92 : 4
х = 23 (дм) — длина второй стороны треугольника.
Найдём длину других сторон треугольника:
2х = 2 • 23 = 46 (дм) — длина первой стороны треугольника.
х + 7 = 23 + 7 = 30 (дм) — длина третьей стороны треугольника.
Ответ: длина первой стороны треугольника 46 дм, второй — 23 дм, а третьей — 30 дм.
509. 1) Верно ли, что если каждое слагаемое делится на некоторое число, то и сумма этих слагаемых делится на это число? Проиллюстрируйте свой ответ примерами.
Это утверждение верно, что можно подтвердить примерами:
2) Может ли сумма нескольких слагаемых делиться на некоторое число, если каждое слагаемое не делится на это число? Проиллюстрируйте свой ответ примерами.
Это утверждение верно, что можно подтвердить примерами:
510. Как изменится частное, если:
511. Делимое увеличили в 3 раза. Как надо изменить делитель, чтобы частное:
512. При каких значениях а верно равенство:
513. Вычислите удобным способом:
514. Вычислите удобным способом:
515. Расставьте в записи 7 • 9 + 12 : 3 — 2 скобки так, чтобы значение полученного выражения было равно:
1) 75: 7 • 9 + 12 : (3 — 2) = 63 + 12 : 1 = 63 + 12 = 75
2) 23: (7 • 9 + 12) : 3 — 2 = (63 + 12) : 3 — 2 = 75 : 3 — 2 = 25 — 2 = 23
516. Расставьте в записи 4 • 12 + 18 : 6 + 3 скобки так, чтобы значение полученного выражения было равно:
1) 50: 4 • 12 + 18 : (6 + 3) = 48 + 18 : 9 = 48 + 2 = 50
2) 72: 4 • (12 + 18 : 6 + 3) = 4 • (12 + 3 + 3) = 4 • 18 = 72
517. Составьте числовое выражение с использованием только знаков четырёх арифметических действий и четырёх цифр 2 так, чтобы значение полученного выражения было равно:
1) 1: 2 : 2 + (2 — 2) = 1 +0 = 1
2) 2: 2 : 2 + 2 : 2 = 1 + 1 = 2
3) 3: 2 • 2 — 2 : 2 = 4 — 1 = 3
4) 4: 2 • (2 : 2) + 2 = 2 • 1 + 2 = 4
5) 5: 2 • 2 + 2 : 2 = 4 + 1 = 5
6) 6: (2 : 2 + 2) • 2 = (1 + 2) • 2 = 3 • 2 = 6
7) 8: 2 + 2 + 2 + 2 = 8
8) 10: 2 • 2 • 2 + 2 = 4 • 2 + 2 = 8 + 2 = 10
Упражнения для повторения
518. Периметр четырёхугольника ABCD равен 34 см, АВ = 6 см, сторона ВС в 2 раза больше стороны АВ, стороны CD и AD равны. Вычислите длину стороны AD.
1) 6 • 2 = 12 (см) — длина стороны ВС.
2) 6 + 12 = 18 (см) — сумма длин сторон АВ и ВС.
3) 34 — 18 = 16 (см) — сумма длин сторон CD и AD.
4) 16 : 2 = 8 (см) — длина каждой из сторон CD и AD.
Ответ: AD = 8 см.
519. Купили розовые и зелёные конверты. Розовых среди них было 18 конвертов. С марками было 12 конвертов, из них 8 были розовыми. Сколько всего купили конвертов, если все зелёные конверты были с марками?
1) 12 — 8 = 4 (шт) — зелёные конверты.
2) 18 + 4 = 22 (шт) — конвертов всего.
Ответ: всего купили 22 конверта.
Задача от мудрой совы
520. На столе расположено семь зубчатых колёс так, что первое сцеплено со вторым, второе — с третьим и т. д., а седьмое сцеплено с первым. Могут ли все колёса вращаться одновременно?
Представим, что выложили в ряд все семь зубчатых колёс и попробовали их вращать. Тогда:
Если мы сцепим первое колесо в седьмым, то получиться, что первое и седьмое колесо — нечётные и будут вращаться в одну сторону. Это невозможно, так как для того, чтобы все колёса вращались одновременно необходимо, чтобы соседние колёса вращались в разные стороны.
Значит в случае с семью зубчатыми колёсами одновременное вращение невозможно.
Это утверждение справедливо и для любого другого нечётного числа зубчатых колёс. Для того, чтобы сцепленные в единую цепочку зубчатые колёса вращались одновременно, необходимо чётное количество таких колёс.