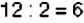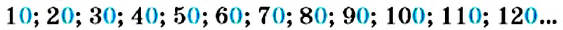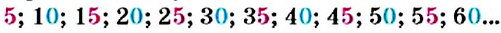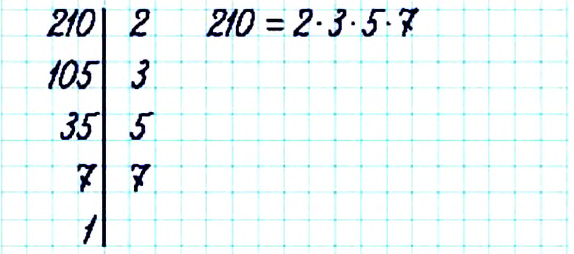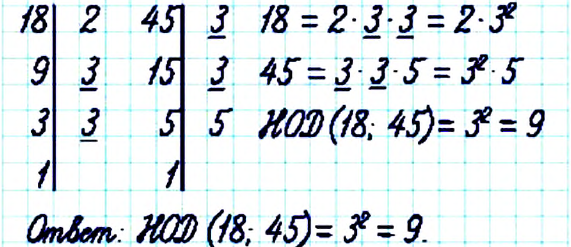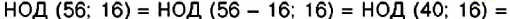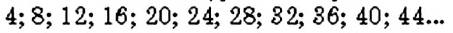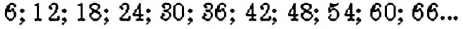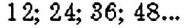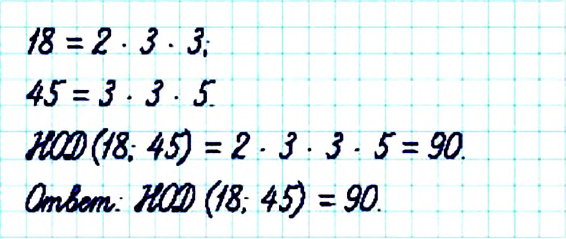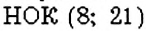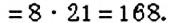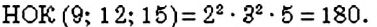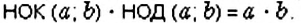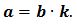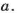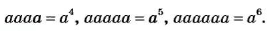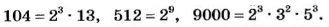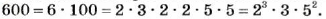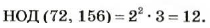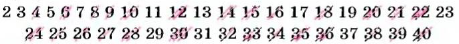На что делится число 266
Информация о числах
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел.
Сейчас изучают числа:
Число 266
Двести шестьдесят шесть
RGB(0, 1, 10) или #00010A
(возможное основание)
свобода, движение, разнообразие, приключения, путешествия, риск, опасность, страх
Описание числа 266
Положительное вещественное трёхзначное четное число 266 является составным числом. Произведение всех цифр: 72. Делители числа: 1, 2, 7, 14, 19, 38, 133, 266. Сумма делителей: 480. Обратное число для 266 — это 0.0037593984962406013.
Это число представляется произведением: 2 * 7 * 19.
266 (число)
двести шестьдесят шесть
266 (Двести шестьдесят шесть) — натуральное число между 265 и 267.
В математике
В других областях
Полезное
Смотреть что такое «266 (число)» в других словарях:
Число координатное — химических соединений — Термин введен в науку А. Вернером, который предполагает, что ему удалось открыть закономерность, определяющую состав гидратов, аммиакатов (ср. Кобальтиаковые соединения), двойных (и простых, кислородсодержащих) солей и вообще неорганических и… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
265 (число) — 265 двести шестьдесят пять 262 · 263 · 264 · 265 · 266 · 267 · 268 Факторизация: 5×53 Римская запись: CCLXV Двоичное: 100001001 Восьмеричное: 409 Шестнадцатеричное: 109 … Википедия
200 (число) — 200 двести 197 · 198 · 199 · 200 · 201 · 202 · 203 170 · 180 · 190 · 200 · 210 · 220 · 230 100 · 0 · 100 · 200 · 300 · 400 · 500 … Википедия
NGC 266 — Галактика … Википедия
182 (число) — 182 сто восемьдесят два 179 · 180 · 181 · 182 · 183 · 184 · 185 Факторизация: Римская запись: CLXXXII Двоичное: 10110110 Восьмеричное: 266 … Википедия
267 (число) — 267 двести шестьдесят семь 264 · 265 · 266 · 267 · 268 · 269 · 270 Факторизация: 3×89 Римская запись: CCLXVII Двоичное: 100001011 Восьмеричное: 411 Шестнадцатеричное: 10B … Википедия
1709 (число) — 1709 тысяча семьсот девять 1706 · 1707 · 1708 · 1709 · 1710 · 1711 · 1712 Факторизация: Простое Римская запись: Двоичное: 11010101101 Восьмеричное: 3255 Шестнадцатеричное: 6AD Натуральные числа … Википедия
Нумерологический профиль числа 266
Люди, которые резонируют с числом 266, очень лелеют и заботятся о природе. Они любят заботиться о других и заботиться о них, особенно о своих близких.
Толкование
Поскольку вы в настоящее время читаете эту статью, вы пришли к выводу, что вы хотите узнать значение числа 266. Вероятно, вы неоднократно видите это число и начинаете задумываться о его значении.
Нет причин для беспокойства. Ваши ангелы-хранители пытаются связаться с вами и предоставить вам некоторую информацию, касающуюся ваших текущих жизненных обстоятельств. Они делают это, привлекая ваше внимание, показывая вам одинаковые цифры или последовательности цифр. Сообщение, которое они хотят донести до вас, скрыто в символике числа, которое вы продолжаете видеть.
По цифрам
В тексте ниже вы можете узнать больше о символическом значении ангела 266. Число 266 является комбинацией энергий чисел 2 и 6. Число 6 появляется в этом числе дважды, и его влияние усиливается.
Число 2 символизирует партнерство, отношения, любовь, командную работу, самоотверженность, стабильность, адаптивность, гармонию, мир, баланс, служение и помощь другим. Число 2 также символизирует открытие и служение цели и миссии вашей Божественной души в этой жизни, миролюбие и великодушие. Она сильно связана с интуицией и восприятием человеческой души. Двойка в нумерологическом профиле позволяет отредактировать состояние покоя внутреннего мира. Малейшее нарушение состояния равновесия мгновенно провоцирует на действия.
Число 6 символизирует стабильность, самоотверженность, служение другим, дом, благодарность, благодать, семью, обеспечение материальных потребностей, заботу, заботу, ответственность и надежность, поиск решений проблем и преодоление препятствий. Цифра является символом гармонии, которая олицетворяет мужское и женское начало, круг жизни. Рожденный под цифрой шесть, добрый и ответственный человек. Часто такие люди обладают многими талантами и способностью жить в гармонии с окружающим миром.
По сумме
Число 266, как смесь всех этих энергий, символизирует создание баланса и гармонии в вашем доме и семейной жизни. Это также символизирует обеспечение материальных потребностей вашей семьи, а также ваших собственных. Это число символизирует служение другим, заботу, воспитание, ответственность, отношения, семью, дом, баланс, стабильность, благодарность и надежность.
Значение числа 14. Это кармическое число. Человеку в чьем нумерологическом профиле присутствует 14 необходимо развивать умение нести ответственность за все свои поступки. Эта цифра сдержанности и педантичности.
Значение цифры 5. Пятерка может серьезно влиять на судьбу человека в любом измерении. Это символ предпринимателя, который всегда во всем ищет прибыль. Пятерка любит долгие и дальние поездки и находится в постоянном поиске.
Магия пятерки имеет влияние на все сферы жизни человека, рожденного в пятый день месяца.
Послание числа – это сообщение от ваших ангелов-хранителей, в котором вас просят верить, что Вселенная будет удовлетворять ваши материальные потребности, пока вы находитесь на пути раскрытия своего истинного пути и цели в этой жизни.
Поверьте, что вскоре вы будете вознаграждены Вселенной за хорошую работу и усилия, которые вы уже проделали.
Характеристики личности
Послание, зашифрованное в числе 266, имеет влияние на сферу денег и увлечений. Оно указывает на то, что упорство в стремлении быть независимым скоро принесет долгожданные плоды в виде финансов.
Люди, которые резонируют с числом 266, являются любящими и сострадательными партнерами. Им людям нравится быть в преданных отношениях и преданными и преданными партнерами. Они уважают своих партнеров и отношения с ними. Эти люди очень привязаны к своим семьям и своим домам и любят проводить там время с членами своей семьи. Они заботливые и заботливые партнеры и родители.
266=2+6+6=14=1+4=5. Пять волн, которые испускает пространство в вечность. Так человек познает мир вокруг и выбираете язык вселенной. Пять волн, которые испускает пространство в вечность. Так человек познает мир вокруг и выбираете язык вселенной.
Положительные
Число 266 – это смесь влияний чисел 2 и 6 и числа 5, потому что это сумма всех трех чисел (2 + 6 + 6 = 14 = 1 + 4 = 5). Число 6 появляется дважды, и это усиливает его влияние.
Число 2 символизирует адаптивность, двойственность, сервис, баланс, отношения, гармонию, стабильность, честность, доверие, веру, сострадание, сотрудничество, компромисс, партнерство, командную работу и дипломатию.
Число 6 символизирует дом, равновесие, стабильность, семью, любовь, надежность, ответственность, обеспечение себя и других, воспитание, заботу и служение другим.
Шестерка – это союз двух треугольников. Такой знак известен, как щит Давида.
Отрицательные
Как сочетание этих влияний, число 266 символизирует внесение серьезных изменений и принятие важных решений, чтобы обеспечить себя и свою семью.
Этот номер также символизирует создание баланса и гармонии в вашем доме и семейной жизни. Этот номер символизирует служение другим и компромисс. Главные проблемы – недоверие, неверие в добро, желание скрыть свои чувства. Излишняя подозрительность к людям и реализм, граничащий с пессимизмом. Научитесь верить в счастливый случай, иначе упустите возможность удачи.
Что предвещает?
Послание толкуется как знак сбалансированности и стабильности. Наслаждайтесь домашней и семейной жизнью, оставаясь предприимчивым и креативным. Служите и помогайте дорогим и любимым людям. Будьте честны и правдивы. Этим вы вселите уверенность в других.
Ваше дружелюбие, эмпатия, нестандартность мышления скоро будут кстати, и кто-то готов выплатить вам немало денежных знаков за присутствие в команде. Приложите все усилия, чтобы не прогнуться и не утратить самое ценное качество своего характера, и ваши успехи возрастут.
Возможно, вы перегружены слишком большими обязанностями, особенно связанными с обеспечением и воспитанием ваших близких. Вы должны взять некоторое время, чтобы быть самостоятельно, занимаясь тем, что вам лично нравится. Найдите время для отдыха и расслабления.
Если при погружении в сон вы увидели число 226 это означает, что в скором времени вас ждет важное событие, которое перевернет всю жизнь и поможет обрести гармонию.
Скрытое число 260х6=1560=1+5+6+0=120=1+2+0=30. Указывает на огонь, который постоянно истекает из ваших мыслей с высокой скоростью.
В ангельской нумерологии тайное значение числа 266=200х66=13200=1+3+2+00=600, говорит о том, что только сильный человек может увеличить свою душевность и достичь регенерации и заживления клеток выше, чем в обыденной жизни.
Послание ангелов
Также будьте благодарны за все благословения, которые вы имеете в жизни, и те, которые приходят. Если ангел с номером 266 часто появляется в вашей жизни, это может быть сообщением о серьезных жизненных изменениях, которые скоро произойдут в вашей жизни.
Двойка, закодированная в послании ангелов, указывает на то, что пора вспомнить об умении находить компромисс в спорной ситуации. Скоро вы столкнетесь с необходимостью выбирать и, если вы выберите правильно, избежите негатива.
Две шестерки в ангельском послании означают, что вы в не в ладах со своими мыслями и занимаетесь нелюбимым делом, вы утратили баланс между душой и разумом. Ангелы просят вернуться в ваше обычное состояние, и вы будете довольны результатом.
Ваши ангелы-хранители готовят вас к этим событиям и просят вас поверить, что эти изменения принесут вам наибольшую пользу. Они просят вас обнять их и попытаться адаптировать их как можно скорее. Ангелы просят вас призвать их, если у вас начнутся сомнения и заботы о будущем, когда начнутся эти изменения.
РЕКОМЕНДУЮ проверенные курсы:
Введение в чакрамную систему> Как научиться чувствовать энергетическую систему и использовать каждую чакру для улучшения любой области жизни.
Медитации от Василия Попова> Избавьтесь от стресса и улучшите самочувствие всего за 10 мин. в день.
Мудры. Магия жестов> Как получать подсказки и поддержку Высших Сил через гармоничную связь с высокочастотным энергетическим потоком.
Искусство ТАРО> Познайте тайны древних жрецов и освойте новую профессию!
Секреты РУН> Получите опыт работы с инструментами далёкого прошлого для трансформации Своего настоящего и будущего.
Руническая защита от коронавируса> Освойте техники, которые позволят выстроить эффективную защиту против вирусных инфекций.
Исполнение желаний> Психотехнологии для достижения целей. Исполнение мечты – это не чудо, а следствие грамотно выстроенных действий!
Кармические задачи в коде вашего рождения> Причины ваших неудач, денежных и других ограничений и блокировок.
Содержание:
Делимость натуральных чисел
Делители и кратные натурального числа. простые числа
Посмотрите на рисунок 1. Вы видите, что 6 яблок разделили на 2 кучки по 3 яблока в каждой. Тут число 6 является делимым, число 2 — делителем, а число 3 — частным. Однако 6 яблок можно разделить и иначе — разложить их на 3 кучки по 2 яблока в каждой. Тогда для делимого 6 число 3 является делителем, а число 2 — частным. Это значит, что числа 2 и 3 являются делителями числа 6. В то же время число 6 является кратным для каждого из своих делителей — и для числа 2, и для числа 3. Делители и кратные являются натуральными числами.
Определение:
Делителем числа называется такое число, на которое делится данное число.
Kpaтным числа называется такое число, которое делится на данное число.
Пример:
Есть ли другие делители у числа 6? Да. Число 6 делится ещё на 1 и само на себя. Значит, всего у числа 6 есть четыре делителя: 1; 2;3;6.
Обратите внимание:
каждое натуральное число, начиная с числа 2. имеет по меньшей мере два делителя — число 1 и само это число. Другие делители находят по специальным правилам.
Пример:
Найдите все делители числа: 1) 7; 2) 12; 3)25.
Решение:
1) У числа 7 есть по меньшей мере два делителя — 1 и 7. Ни на одно другое натуральное число 7 не делится, поэтому у него всего два делителя: 1 и 7.
2) Число 12 имеет по меньшей мере два делителя — 1 и 2. Далее последовательно проверяем делимость числа 12 на натуральные числа от 2 до 11.
3) У числа 25 есть как минимум два делителя: 1 и 25 На 2, 3 и 4, а также на числа от 6 до 24 это число не делится.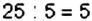 
, поэтому число 5 является делителем числа 25, причём дважды. Однако равные делители учитываются только один раз. Значит, у числа 25 не четыре, а три делителя: 1; 5; 25.
Запомните: Натуральное число, у которого есть только два делителя (1 и само число), называется простым. Натуральное число, у которого больше двух делителей, называется составным.
Например, 7 — простое число, а 12 и 25 — составные.
Пример:
Является ли 1 простым числом? А составным? Нет, поскольку у числа 1 только один делитель. Значит, число 1 особенное. Оно и не простое, и не составное.
Обратите внимание:
наименьшим простым числом является число 2.
Чтобы выписать некоторое количество простых чисел, можно воспользоваться способом, придуманным ещё в III в до н.э. Эратосфеном Киренским (27бг. до н. э. — 194 г. до н. э ). греческим математиком, астрономом, географом и поэтом. В честь учёного этот способ называется «решето Эратосфена». На рисунке (с. 4) вы видите, как находили простые числа от 2 до 50. Попробуйте самостоятельно объяснить, как это делали.
Признаки делимости на 2, 10, 5
Запишем натуральный ряд чисел:
1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12.
Умножим каждое число на 2. Получили ряд чисел, кратных числу 2:
2; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24.
Такие числа называют чётными. Их можно задать формулой:
, где 
— некоторое натуральное число. Цифры О, 2, 4, 6, 8 считают чётными цифрами.
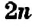
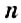
В натуральном ряде чётные числа чередуются с нечётными числами — они не делятся на 2. Например, числа 3, 5, 11 — нечётные. Их также можно задать формулой:
, где — некоторое натуральное число. Цифры 1, 3, 5, 7, 9 считают нечётными цифрами.
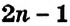
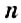
Пример:
Как выяснить, является ли чётным данное число? Для этого пользуются признаком делимости на 2.
Признак делимости на 2
На 2 делятся те и только те числа, запись которых заканчивается чётной цифрой.
Например, запись числа 538 заканчивается цифрой 8, которая является чётной, поэтому число 538 делится на 2. Действительно,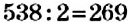 
. А вот запись числа 537 закапывается нечётной цифрой 7, поэтому данное число не делится на 2.
Опираясь на натуральный ряд чисел, запишем ряд чисел, кратных числу 10:
Как видим, запись каждого числа этого ряда заканчивается цифрой 0. Именно в этом и состоит признак делимости на 10.
Признак делимости на 10
На 10 делятся те и только те числа, запись которых заканчивается цифрой 0.
Например, число 1000 делится на 10, а число 1001 не делится.
Пример:
Можно ли считать признак делимости на 10 признаком делимости на 5? Нет, так как существуют числа, которые делятся на 5, но не делятся на 10. Например, число 2055.
Опираясь на натуральный ряд чисел, запишем ряд чисел, кратных числу 5:
Как видим, запись каждого числа этого ряда заканчивается либо цифрой 5, либо цифрой 0. Именно в этом и состоит признак делимости на 5.
Признак делимости на 5
На 5 делятся те и только те числа, запись которых заканчивается либо цифрой 5, либо цифрой 0.
Пример:
Найдите все нечётные числа от 10 до 40, которые делятся на 5.
Решение:
Способ 1. Сначала выберем все нечётные числа от 10 до 40:
.
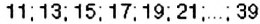
Применив к этим числам признак делимости на 5, получим искомые числа: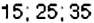 
.
Способ 2. Искомые числа — нечётные и делятся на 5. Поэтому : среди них не должно быть чисел, запись которых заканчивается цифрой 0. поскольку такие числа — чётные. Итак, среди чисел от : 10 до 40 достаточно выбрать числа, запись которых заканчивается только цифрой 5. Отсюда искомым и будут числа: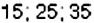 
.
Обратите внимание:
среди чисел, делящихся на 5. чётные числа делятся и на 10. а нечётные — нет.
Признак делимости на 4. Число делится на 4 тогда и только тогда, когда на 4 делится число, образованное двумя последними цифрами данного числа. Например, число 3436 делится на 4, поскольку число 36 делится на 4.
Признак делимости на 8. Число делится на 8 тогда и только тогда, когда на 8 делится число, образованное тремя последними цифрами данного числа. Например, число 29176 делится на 8, поскольку число 176 делится на 8.
Признак делимости на 25. Число делится на 25 тогда и только тогда, когда на 25 делится число, образованное двумя последними цифрами данного числа Например, число 6575 делится на 25, поскольку число 75 делится на 25.
Признак делимости на 125. Число делится на 125 тогда и только тогда, когда на 125 делится число, образованное тремя последними цифрами данного числа. Например, число 36 375 делится на 125, поскольку число 375 делится на 125.
Признаки делимости на 9, 3
Запишем ряд чисел, кратных числу 9:
.
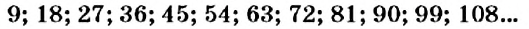
Как видим, признак делимости на 9 не связан с последней цифрой в записи числа. Он связан с сумой цифр в этой записи. Позже вы сможете это обосновать.
Признак делимости на 9
На 9 делятся те и только те числа, сумма цифр которых делится на 9.
Например, число 1476 делится на 9, поскольку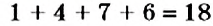 
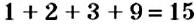
, а число 18 делится на 9. Число 1239 не делится на 9, поскольку 
, а число 15 не делится на 9.
Пример:
Как выяснить, делится ли число на 3? Для этого пользуются признаком делимости на 3.
Признак делимости на 3
На 3 делятся те и только те числа, сумма цифр которых делится на 3.
Например, в числе 237 сумма цифр равна: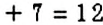 
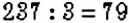
. Число 12 делится на 3, поэтому и число 237 делится на 3. Действительно, 
.
Пример:
Можно ли считать, что числа, которые делятся на 9, делятся и на 3? Да. Поскольку сумма цифр чисел, кратных числу 9, делится на 9, то она делится и на 3. Однако обратное утверждение не будет верным: числа, которые делятся на 3, не всегда делятся на 9. Например, числа 12, 33, 213 делятся на 3, но не делятся на 9.
Пример:
Найдите все трёхзначные числа, которые содержат цифры 5 и 1 и делятся на 9.
Решение:
Обозначим неизвестную цифру звездочкой. Сумма цифр искомого числа равна: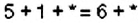 
. Эта сумма должна делиться на 9, поэтому вместо звёздочки можно подставить только цифру 3. А далее из цифр 1, 3, 5 составляем все возможные трёхзначные числа: 135; 153; 315; 351; 513; 531.
У вас мог возникнуть вопрос: «Как объяснить, почему сумма цифр в записи числа может показывать, делится ли число на 9?» Разберёмся на примерах.
Числа 99 и 999 делятся на 9, а числа 100 и 1000 на 9 не делятся. Представим эти числа в виде сумм:
Проанализируем полученные суммы. В столбике слева каждое слагаемое суммы делится на 9, а в столбике справа — нет. Вообще, если каждое слагаемое делится на данное число, то их сумма делится на данное число; если одно из слагаемых не делится на данное число, а сумма всех остальных слагаемых делится на данное число, то сумма не делится на данное число. Запишем число 351 в виде суммы разрядных слагаемых и преобразуем её:
В полученной сумме каждое слагаемое делится на 9, поэтому число 351 делится на 9. Как видим, результат зависит от последнего слагаемого, которое получили как сумму: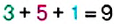 
. Эта сумма — не что иное, как сумма цифр данного числа.
Разложение чисел на множители. Наибольший общий делитель
Вы знаете, что каждое натуральное число, большее 1, имеет несколько делителей, поэтому его можно представить в виде произведения своих делителей. Например: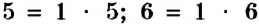 
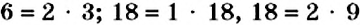
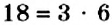
, или 
, или 
. О таких равенствах говорят, что данное число разложили на множители, а само равенство называют разложением числа на множители.
Число 5 — простое. Его можно разложить на множители только одним способом. Числа 6 и 18 — составные. Для них существует два и более разложений на множители. Однако эти разложения отличаются. В разложении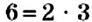 
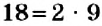
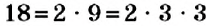
оба множителя являются простыми числами, а в разложении 
первый множитель — простое число, а второй — составное, и его тоже можно разложить на множители: 
. А уже в этом разложении все множители являются простыми числами.
Определение:
Разложение числа на множители, в котором все множители — простые числа, называется разложением числа на простые множители.
Пример:
Является ли разложением на простые множители равенство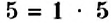 
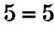
? Нет. В этом разложении один из множителей не является простым. Это число 1. Однако будем считать, что для любого простого числа также можно записать разложение на простые множители. Для этого достаточно записать в разложении само это число. Например, для данного простого числа 5 получим такое разложение: 
.
Пример:
Разложите на простые множители число 210.
Решение:
С помощью разложения числа на простые множители ищут общие делители двух чисел. Например, у чисел 12 и 30 есть два простых общих делителя — числа 2 и 3. Но числа 12 и 30 делятся и на число 6, то есть на произведение своих общих делителей. Число 6 — наибольшее число, на которое одновременно делится и число 12, и число 30. Такое число называют наибольшим общим делителем двух чисел 12 и 30.
Записывают: НОД 
и говорят: «Наибольшим общим делителем чисел 12 и 30 является число 6».
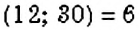
Пример:
Найдите НОД чисел 18 и 45.
Решение:
Определение:
Наибольшим общим делителем двух чисел называется наибольшее число, на которое делится каждое из данных чисел.
Правило нахождения НОД
Чтобы найти НОД двух чисел:
1) разложите данные числа на простые множители;
2) найдите произведение общих делителей данных чисел.
Пример:
Можно ли найти НОД двух чисел, не имеющих общих делителей, кроме числа 1? Да. Но НОД таких чисел равен 1.
Два числа, НОД которых равен 1, называют взаимно простыми. Например, 
. Значит, числа 8 и 21 — взаимно простые. Два разных простых числа также являются взаимно простыми. Например,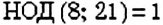 
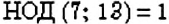
, поэтому простые числа 7 и 13 являются взаимно простыми.
Пример:
Можно ли найти НОД нескольких чисел? Да. Для этого выполняют те же действия, что и в задаче 3, но для нескольких чисел. Например, найдём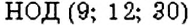 
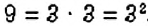
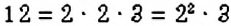
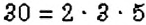
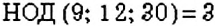
. Имеем: 
, 
, 
. Следовательно, 
.
Например, 
Наименьшее общее кратное
Найдём кратные числа 4. Для этого достаточно умножить число 4 на числа натурального ряда:
Аналогично найдём кратные числа 6:
Среди кратных числа 4 и числа 6 есть такие числа, которые делятся на оба данных числа:
Эти числа являются общими кратными чисел 4 и 6. Наименьшим среди них является число 12. Это — наименьшее общее кратное двух чисел 4 и 6.
Записывают: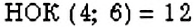 
и говорят: «Наименьшим общим кратным чисел 4 и 6 является число 12».
Определение:
Наименьшим общим кратным двух чисел называется наименьшее число, которое делится на каждое из данных чисел.
Общие кратные нескольких чисел можно находить при помощи разложений данных чисел на простые множители.
Пример:
Найдите НОК чисел 18 и 45.
Решение:
Правило находжения НОК
Чтобы найти НОК двух чисел:
Пример:
Как найти НОК двух взаимно простых чисел? Нескольких чисел?
Поскольку у взаимно простых чисел нет других общих делителей, кроме 1, то НОК взаимно простых чисел равно их произведению. Например, 
НОК нескольких чисел находят так же, как и двух чисел. Например, найдём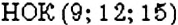 
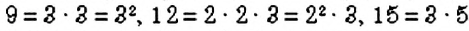
. Имеем: 
. 
Оказывается, между НОК и НОД чисел 
и 
существует связь:
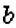
Например, для чисел 54 и 48 получим:
.
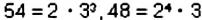
Отсюда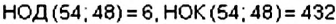 
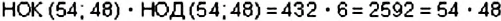
. А теперь воспользуемся формулой. Имеем:
.
Делимость натуральных чисел
В этом разделе рассматриваются важнейшие сведения из теории чисел. Это очень древняя и интересная математическая наука, которая исследует свойства натуральных чисел, связанные с их делением. Кратко основное содержание раздела выглядит так.
Эти темы часто используются в последующих разделах математики. В частности, без их знания невозможно успешно изучать обыкновенные дроби. Поэтому раздел 1 учебника можно считать введением к разделу 2.
Деление и делители числа
20 : 4 = 5, потому что 5*4 = 20.
Разделить одно число на другое — значит найти такое третье число, которое при умножении на второе дает первое число. То есть, если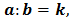 
то 
Вы уже знаете, что иногда при делении одного числа на другое получают неполное частное и остаток. Вы также знаете, что делить можно и дробные числа. В этом разделе мы будем рассматривать деление только натуральных чисел, причем без остатка.
Например, число 21 делится на 7. Говорят, что число 7 является делителем числа 21. Делителями числа 21 являются также числа 1, 3 и 21. Никакое другое число не является делителем числа 21.
Если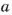 
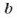
делится на 
то число 
называют делителем числа 
Например, число 22 имеет четыре делителя: 1,2,11 и 22;
Число, которое имеет только два делителя, называется простым числом. Можно сказать и так. Число, которое делится только на 1 и само на себя, называется простым.
Число, имеющее больше двух делителей, называется составным.
Простое 7 = 1-7.
Составное 14=1-2-7.
1 — не простое и не составное.
Составными, например, являются числа 4, (5, 8, 9, 10, 12, 14. Составных чисел также бесконечно много.
Число 1 имеет только один делитель: 1. Его не принято называть ни простым, ни составным числом.
В зависимости от количества делителей все натуральные числа делятся на три класса: простые числа, составные числа, число 1.
Если простые числа записать в порядке их возрастания, то образуется последовательность простых чисел:
Последовательность простых чисел имеет много интересных свойств и тайн. Например, еще ученые Древней Греции заметили, что среди простых чисел много таких, разность которых равна 2, например: 3 и 5, 5 и 7, 11 и 13, 17 и 10 и т. д. Такие пары чисел называются простыми числами близнецами.
Уже более 25 веков математики пытаются выяснить, существуют ли наибольшие числа-близнецы, но и до сих пор ответа на этот вопрос мы не знаем.
Существует также много других проблем (еще не решенных задач), связанных с простыми числами.
Выполнение заданий:
Пример №1
Проверьте, является ли число 7 делителем числа 63. А числа 67?
Решение:
Пример №2
Найдите наибольший делитель и наибольший простой делитель числа 20.
Решение:
Признаки делимости на 10, 5 и 2
Как узнать, делится ли то или иное число на 10? Очень легко. Нужно лишь посмотреть на его последнюю цифру. Если она 0, то данное число делится на 10. Если же последняя цифра не 0, то это число на 10 не делится. Два последние предложения можно заменить одним, которое называется признаком делимости чисел на 10.
На 10 делятся все те и только те числа, которые оканчиваются цифрой 0.
Используя этот признак, можно сразу (не выполняя деления) сказать, что числа 130, 3700, 4080 делятся на 10, а числа 83, 305, 1001 на 10 не делятся.
Признак делимости на 5 можно сформулировать так.
На 5 делятся все те и только те числа, которые оканчиваются цифрой 5 или 0.
Например, каждое из чисел 95, 375, 70, 4900 делится на 5, а каждою из чисел 37, 559, 5008 на 5 не делится. Убедитесь в этом, разделив каждое из этих чисел на 5.
На 2 делится каждое натуральное число, которое оканчивается цифрой 0, 2, 4, 6 или 8. Эти цифры называют четными. Поэтому признак делимости на 2 можно сформулировать так.
На 2 делятся все те и только те числа, которые оканчиваются четной цифрой.
Примеры чисел, которые делятся на 2:
0, 2, 4, 6, 8, 10, 12, 14, 16, 376, 11 108.
Числа, которые делятся на 2, называются четными.
Выполнение заданий:
Пример №3
Найдите наибольшее четное трехзначное число.
Решение:
Пример №4
Сколько существует нечетных чисел, которые больше 90 и меньше 100?
Решение:
Такими являются числа 91,93, 95, 97 и 99. Их всего 5.
Пример №5
Решение:
Если числа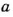 
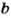
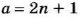
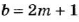
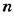
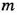
и 
нечетные, то 
и 
, где 
и 
— некоторые натуральные числа.
Тогда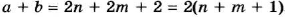 
, а это число четное.
Признаки делимости на 3 и 9
Чтобы узнать, делится число на 3 или нет, находят его сумму цифр. Например, сумма цифр числа 21 204 равна 9, поскольку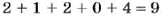 
. Оказывается, что если сумма цифр числа делится на 3, то и само число делится на 3. Если же сумма цифр числа на 3 не делится, то и число на 3 не делится. Это признак делимости на 3.
На 3 делятся все те и только те числа, сумма цифр которых делится на 3.
Примеры: Сумма цифр числа 31 104 равна 9, а 9 делится на 3, поэтому и число 31 104 делится на 3. Сумма цифр числа 5051 равна 11, она не делится на 3. Поэтому и число 5051 па 3 не делится. Проверьте!
Аналогично формулируется и признак делимости на 9.
На 9 делятся все те и только те числа, сумма цифр которых делится на 9.
Примеры: Число 5742 делится на 9, поскольку сумма его цифр 5 + 7 + 4 + 2 = 18, а 18 делится на 9. А число 5051 на 9 не делится, так как его сумма цифр 5 + 0 + 5+1 = 11, а 11 на 9 не делится.
Каждое число, которое делится на 9, называется кратным числа 9. Каждое число, которое делится на 3, называется кратным числа 3.
Вообще, если одно число делится на другое, то первое называется кратным другого.
Говорят: «кратное трех», но «кратно трем».
Если число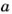 
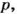
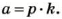
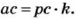
делится на 
то 
Тогда и 
Здесь все буквы обозначают натуральные числа. Итак, если один из множителей делится на какое-то число, то и произведение этих множителей делится на это же число.
Если каждое из чисел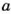 
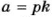
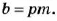
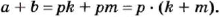
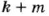
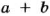
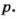
и 
делится на 
то 
и 
Поэтому 
Число 
натуральное, тогда число 
также делится на 
Следовательно, если каждое из двух слагаемых делится на какое-то число, то и их сумма делится па это число.
О признаках делимости на 4,6, 7,11,13 читайте на с. 37.
Выполнение заданий:
Пример №6
Какое утверждение верно:
а) если число делится на 9, то оно делится и на 3.
б) если число делится на 3, то оно делится и на 9?
Решение:
Если число делится на 9, то сумма его цифр делится на 9. Эта сумма делится и на 3. Поэтому первое утверждение верно.
Второе утверждение неверно. Например, 30 делится на 3, но не делится на 9.
Пример №7
Запишите наибольшее четырехзначное число, которое кратно 3, но не кратно 9.
Решение:
Наибольшее четырехзначное число 9999. Оно делится и на 9, и на 3. Если это число уменьшить на 3, то получим число 9996. Оно кратно 3, но не кратно 9.
Разложение чисел на простые множители
Какие простые числа нужно умножить, чтобы получить 15? Нетрудно догадаться, что такими числами являются 3 и 5. Следовательно, 15 = 3 • 5. Такое представление числа 15 называется его разложением на простые множители.
Другие примеры:
30 = 2 • 3 • 5; 45 = 3 • 3 • 5; 88 = 2 • 2 • 2 • 11.
Каждое составное число можно разложить на два или больше простых множителей.
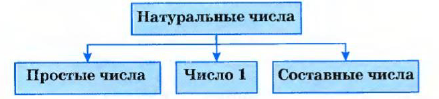
В отдельных случаях разложение числа на простые множители можно упростить. Например, число 9000 на простые множители можно разложить так:
Число 9000 раскладывается на восемь простых множителей. Каждый из них является делителем числа 9000. Вообще, каждый из множителей, на какие раскладывается число а, является делителем этого числа.
Разных простых делителей число 9000 имеет три: 2, 3 и 5. А разных натуральных делителей это число имеет очень много: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 4500, 9000.
Как вы уже знаете, произведение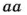 
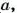
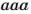
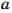
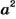
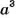
называют квадратом числа 
а произведение 
— кубом числа 
и обозначают 
и 
соответственно.
Аналогично, 
Такие произведения равных чисел называют соответственно четвертой, пятой, шестой степенью числа 
Произведение 
чисел, каждое из которых равно 
, называют 
степенью числа 
и обозначают символом 
. Здесь — степень, — основание степени, 
показатель степени.
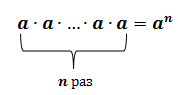
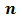
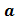
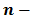
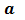
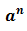
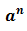
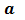
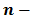
Используя понятие степени, разложение числа на простые множители можно записать короче:
Разложить на простые множители числа, которые делятся на 2, 3, 5, 9, 10, сравнительно несложно. В иных случаях это бывает сделать сложно. Попытайтесь, например, разложить на простые множители число 323. Специалисты, которым часто приходиться заниматься разложением чисел на множители, пользуются специальными таблицами. Часть такой таблицы (для небольших чисел, которые не делятся на 2, 3, 5) представлена на форзаце учебника. Пользуясь этой таблицей, можно сразу записать: 323 = 17 • 19.
Выполнение заданий:
Пример №8
Можно ли разложить на простые множители число 1?
Решение:
Нет, нельзя. Каждое простое число больше 1. А произведение чисел, каждое из которых больше 1, не может равняться 1.
Пример №9
Можно ли равенство 17=1 • 17 считать разложением числа на простые множители?
Решение:
Пример №10
Разложите на простые множители число 600.
Решение:
Пример №11
Разложите на простые множители число 266.
Решение:
Число 266 делится на 2, поэтому 266 = 2 • 133. Число 133 не делится ни на какое из чисел 2, 3, 5. Его нет и в таблице простых чисел. Ищем его в таблице разложения чисел на простые множители: 133 = 7 • 19. Следовательно, 266 = 2 • 7 • 19.
Пример №12
Какое наименьшее трехзначное число можно разложить на два одинаковых простых множителя?
Решение:
Наибольший общий делитель
Часто возникает необходимость находить общие делители двух или нескольких чисел. Попытаемся найти, например, общие делители чисел 30 и 45.
Наибольшим общим делителем (ПОД) нескольких чисел называется наибольшее число, на которое делится каждое из данных чисел.
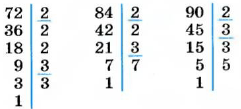
Найдем, например, НОД (72, 84, 90). Разложим каждое из этих чисел на простые множители: 
Числа 72, 84, 90 имеют два общих простых делителя: 2 и 3. Умножив их, получим:
НОД (72, 84, 90) = 2 • 3 = 6.
Чтобы найти наибольший общий делитель нескольких чисел, необходимо разложить их на простые множители и умножить все их общие множители.
Найдем НОД (65, 32). Поскольку
65 = 5 • 13, 32 = 2 • 2 • 2 • 2 • 2,
Два числа, наибольший общий делитель которых равен 1, называются взаимно простыми. Числа 65 и 32 взаимно простыми.
Выполнение заданий:
Пример №13
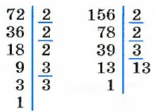
Найдите НОД (72, 156).
Решение:
В разложениях чисел 72 и 156 на простые множители общими являются такие простые множители: 2, 2 и 3.
Поэтому 
Пример №14
Какое наибольшее количество одинаковых букетов можно составить из 6 васильков и 9 ромашек?
Решение:
Необходимо найти наибольшее число, на которое делится 6 и 9, то есть наибольший общий делитель этих чисел. НОД (6, 9) = 3. Следовательно, можно составить 3 букета (рис. 6)
Наименьшее общее кратное
Каждое из этих чисел кратно 8. Любое число, которое делится на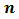 
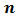
, называется кратным числа 
. Напомним, что речь идет только о натуральных числах и о делении без остатка.
Общими кратными чисел 4 и 6 являются: 12, 24, 36 и много других чисел. Наибольшего общего кратного числа 6 и 4 не имеют. А наименьшее существует.
Наименьшим общим кратным (НОК) нескольких чисел называется такое наименьшее натуральное число, которое делится на каждое данное число. НОК (4, 6) = 12.
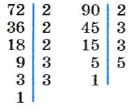
Наименьшее общее кратное двух чисел можно найти, разложив эти числа на простые множители. Найдем, например, НОК (72, 90). Для этого разложим числа 72 и 90 на простые множители. Их НОК должно содержать все простые множители числа 72 и все простые множители числа 90. Следовательно, 35 чтобы найти НОК (72, 90), необходимо простые множители числа 72 дополнить такими простыми множителями числа 90, которых нет в разложении числа 72. В данном случае к произведению 2 • 2 • 2 • 3 • 3 надо дописать множитель 5. Имеем: НОК (72, 90) = 2 • 2 • 2 • 3 • 3 • 5 = 72 • 5 = 360.
Наименьшее общее кратное двух взаимно простых чисел равно их произведению. Например, НОК (5, 8) = 40. Почему?
А как найти НOK трех чисел?
Чтобы найти наименьшее общее кратное чисел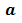 
, 
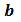
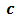
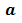
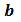
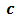
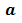
и 
, надо простые множители числа дополнить такими простыми множителями чисел и , которых в нет, и умножить их.
Найдем, например, НОК чисел 72, 90 и 80. Поскольку
то НОК (72, 90, 80) = 2 • 2 • 2 • 3 • 3 • 5 • 2 = 720.
Рассмотрим пример. Пусть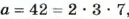 
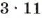
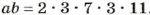
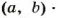
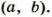
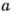
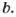
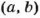
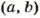
a 
. Их произведение 
. Такое же и произведение НОД 
НОК 
Проверьте! Это свойство верно для любых значений 
и 
Произведение НОД и НОК двух натуральных чисел равно произведению этих чисел. Всегда НОД 
• НОК 
— 
Поэтому, чтобы найти наименьшее общее кратное двух чисел, можно произведение этих чисел разделить на их наибольший общий делитель.
Из этого утверждения вытекают важные следствия:
Выполнение заданий:
Пример №15
Найдите наибольшее двузначное число, кратное чисел 2 и 7.
Решение:
Пример №16
Во время тренировки на стадионе два велосипедиста стартовали одновременно. Первый велосипедист проезжает полный круг за 75 с, а второй — за 100 с. Через какое время велосипедисты вновь встретятся на старте?
Решение:
Искомый интервал времени должен быть кратным чисел 75 и 100. Найдем НОК (75, 100).
75 = 3 • 5 • 5, 100 = 2 • 2 • 5 • 5. IIOK (75, 100) = 100 • 3 = 300. 300 с = 5 мин.
Следовательно, спустя 5 мин велосипедисты вновь встретятся на старте.
Деление натуральных чисел некоторые ученые древности умели выполнять еще несколько тысячелетий назад. Это математическое действие тогда считалось наиболее трудным, поскольку люди не знали современных правил деления, а числа записывали не так, как их записывают теперь. Попытайтесь, например, разделить число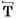 
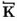
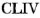
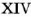
на число 
или 
на 
. Когда-то делили одно число на другое, используя камешки или косточки слив и т. и.
Признаки делимости на 2 и на 9 древнегреческие математики знали еще в III в. до н. э. Только формулировали их не так, как теперь. Издавна известны и другие признаки делимости.
На 4 делятся все те и только те числа, в которых две последние цифры выражают число, которое делится на 4.
На в делятся все те и только те числа, которые делятся и на 2, и на 3.
Простые числа были известны еще в VI в. до н. э. Евклид в III в. до н. э. доказал, что множество простых чисел бесконечно, то есть последовательность
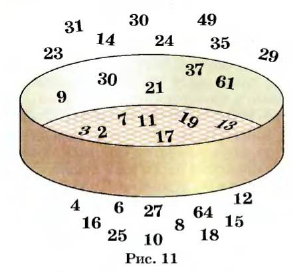
Отсеивание составных чисел образно показано па рисунке 11.
Поэтому такой способ составления таблиц простых чисел назвали «решетом Эратосфена». Ниже показано, как с помощью «решета Эратосфена» можно составить таблицу простых чисел, меньших 40.
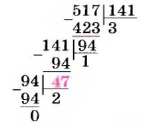
В данном примере НОД (517, 141) = 47. Математики и теперь часто используют этот способ, его называют алгоритмом Евклида.
Главное в разделе:
Если числа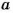 
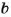
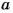
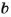
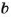
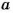
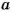
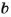
и 
натуральные и 
делится на 
без остатка, то говорят, что 
— делитель числа 
, а 
— кратное числа 
. Например, число 9 имеет три делителя: 1, 3 и 9. Кратных числа 9 бесконечно много: 9, 18, 27.
На 5 делятся все те и только те числа, которые оканчиваются цифрой 5 или 0.
На 10 делятся все те и только те числа, которые оканчиваются цифрой 0.
На 3 делятся все те и только те числа, сумма цифр которых делится на 3.
На 9 делятся все те и только те числа, сумма цифр которых делится на 9.
Если каждое слагаемое делится на некоторое число, то их сумма тоже делится на это число. Если хотя бы один из множителей делится на некоторое число, то и все произведение делится на это число.
Наименьшим общим кратным нескольких чисел (НОК) называют наименьшее натуральное число, которое делится на каждое из данных чисел. Чтобы найти НОК чисел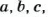 
достаточно разложение на простые множители числа 
дополнить такими простыми множителями чисел 
которых нет в разложении числа 
, и умножить их.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.