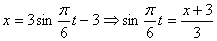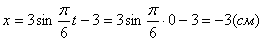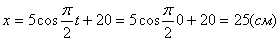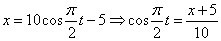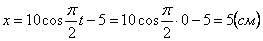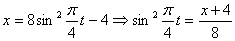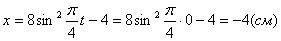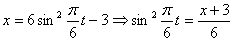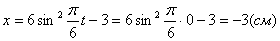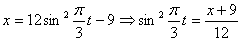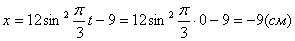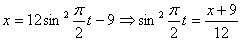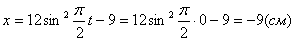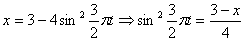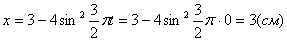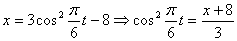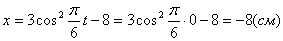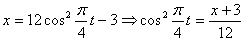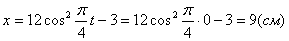Начальное положение точки r 30 чему

|r| = √ 3 ^ 2 + 4 ^ 2 = √ 25 = 5

Тело переместилось в точку с координатами х = 2 и у = 1мю Найдите проекция вектора перемещениях на осях х и у.

Найдите координаты координаты конечного положения тела.

Чему равен его модуль?

Помогите пожалуйста?

Найдите координаты координаты конечного положения тела.

Чему равен его модуль?

Решите пожалуйста задачи?

Решите пожалуйста задачи.

Определите, на какой высоте находится муха.

Модуль вектора гА равен 5 м.

Определите модуль вектора гв и угол, который он составляет с осью ОХ.

Модули векторов равны 3 и 5, 2 м.

Определите модуль полученного вектора и угол, который он составляет с осью OX.

Как определяют положение точки в пространстве?

Как определяют положение точки в пространстве?

Опишите характер движения точки, найдите начальную координату, модуль и направление вектора скорости.

Чему равно ускорение материальной точки?

Какими величинами определяется положение точки на плоскости?

Какими величинами определяется положение точки на плоскости?

Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5?

Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5.

Найдите координаты конечного полодения тела.

Начертите вектор перемещения.

Чему равен его модуль?

Как задают положение точки в пространстве с помощью координат?

Как задают положение точки в пространстве с помощью координат.

Источник

|r| = √ 3 ^ 2 + 4 ^ 2 = √ 25 = 5

Тело переместилось в точку с координатами х = 2 и у = 1мю Найдите проекция вектора перемещениях на осях х и у.

Найдите координаты координаты конечного положения тела.

Чему равен его модуль?

Помогите пожалуйста?

Найдите координаты координаты конечного положения тела.

Чему равен его модуль?

Решите пожалуйста задачи?

Решите пожалуйста задачи.

Определите, на какой высоте находится муха.

Модуль вектора гА равен 5 м.

Определите модуль вектора гв и угол, который он составляет с осью ОХ.

Модули векторов равны 3 и 5, 2 м.

Определите модуль полученного вектора и угол, который он составляет с осью OX.

Как определяют положение точки в пространстве?

Как определяют положение точки в пространстве?

Опишите характер движения точки, найдите начальную координату, модуль и направление вектора скорости.

Чему равно ускорение материальной точки?

Какими величинами определяется положение точки на плоскости?

Какими величинами определяется положение точки на плоскости?

Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5?

Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5.

Найдите координаты конечного полодения тела.

Начертите вектор перемещения.

Чему равен его модуль?

Как задают положение точки в пространстве с помощью координат?

Как задают положение точки в пространстве с помощью координат.

Источник

Уравнение траектории тела — определение и формулы

Изучением движения тела в пространстве занимается большой раздел в физике — кинематика. Причём причины, заставляющие объект двигаться, исследует динамика. Путь, который проходит физическая точка, называют траекторией тела. Уравнение, описывающее этот процесс, зависит от направления, заданного действием, вызывающим изменение её положения. Форма же перемещения определяется выбранной системой координат и местом начального отсчёта.

Общие сведения

Под движением тела понимают процесс его перемещения из одной точки пространства в другую. Произошедшее действие исследуют относительно другого объекта или выбранных начальных координат. При этом положение вовсе не обязательно может изменяться сразу ко всем окружающим его телам. Например, стоящий человек на Земле находится в состоянии покоя по отношению к планете, но движется относительно Солнца.

В физике принято любое изменение определять в системе пространственных координат. За оси принимают перпендикулярные линии x, y, z. Совокупность данных, используемых для изучения движения, называют системой отсчёта.

Существует несколько видов механического перемещения (во времени) физической точки:

При движении тело проходит определённый путь. Описать его можно виртуальной линией, при этом она может быть как прямой, так и кривой. Именно она и называется траекторией движения. По сути, эта линия соединяет последовательно все положения точки в пространстве — от начальной до конечной. Длина отрезка является пройденным путём и считается векторной величиной.

Изменение радиус-вектора r (значения, задающего положение точки в пространстве относительно другого тела) описывает кинематический закон: r = r (t). В трёхмерных декартовых координатах его можно записать так: r = xe + ye + ze = (x, y, z). Вектор, построенный из начальной точки движущегося тела в расположение её в данный момент времени, то есть приращение радиус-вектора за определённый промежуток t, как раз и называют перемещением.

Результирующее движение же равно векторной сумме последовательных изменений положения. При прямолинейном перемещении вектор пути совпадает с соответствующим участком траектории, а модуль перестановки равняется пройденному расстоянию.

Время, за которое тело пройдёт по установленной траектории пути, называют скоростью. Фактически это быстрота изменения координаты. Физики, исследуя передвижение, изучают не только положение материальной точки в начальный и конечный момент времени, но и закон, по которому происходит перемещение. Другими словами, они определяют зависимость радиус-вектора от времени.

Горизонтальное перемещение

Пусть имеется тело, брошенное горизонтально поверхности. Высота падения равняется h, а начальная скорость V0. Здесь систему отсчёта удобно связать с Землёй. Объект будет передвигаться под действием силы тяжести. Остальными силами, например, сопротивлением воздуха, можно пренебречь. Тело перемещается в плоскости, содержащей вектора ускорения и свободного падения (g).

Скорость перемещения рассчитывают по формуле: V = √‎(V 2 x + V 2 y). После подстановки полученных ранее выражений равенство примет вид: V = √‎(V 2 0 + g 2 t 2 ). Отсюда следует, что уравнение для вектора движения материальной точки будет: s (t) = s0 + V0t + (g t 2 ) / 2, где: s0 — смещение тела, соответствующее начальному моменту времени.

Можно сделать вывод, что уравнение траектории не записывается через время, поэтому частица будет и перемещаться обратно по той же самой траектории. Временные отрезки между точками пути будут одинаковы как при прямом, так и при обратном движении.

Каждому положению соответствует определённое значение скорости, которое не зависит от направления перемещения. Нужно отметить, что наибольшей величиной в горизонтальной траектории полёта будет начальная точка.

Движение тела под углом

Свободное падение является частным случаем равноускоренного, то есть на перемещаемый объект действует только сила притяжения. Если физическая точка перемещается, то кривая, которая описывается её радиус-вектором, обозначает пройденный путь. Эту траекторию можно описать некоторой математической функцией.

Итак, вектор скорости точки определяется как производная по времени: V = dr / dt = r. Ускорение же можно найти, продифференцировав скорость: a = dV / dt = d 2 r / dt. Если обозначить производную времени точкой, то формулу можно переписать так: a = V = r.

Для того чтобы вывести формулу, нужно воспользоваться основными выражениями, определяющими проекции:

Чтобы запись зависимости вертикальной оси от горизонтальной была как можно более компактной, соответствующие координаты rx и ry можно обозначить через икс и игрек. Из уравнения, связывающего координатную ось X и время, можно определить t как функцию ординаты. Линейное выражение будет иметь вид: t = x / (Vo * cosa).

В итоге останется два слагаемых. Первое будет линейно по иксу, а второе квадратично. Таким образом, зависимость игрека от икса в уравнении траектории — это парабола (справа стоит квадратичная функция). Она проходит через начало координат. Если верно равенство x = 0, то игрек тоже будет равняться нулю.

Следует обратить внимание на то, что в квадрате стоит отрицательный коэффициент. Известно, что если перед квадратичным слагаемым в уравнении параболы стоит отрицательное число, то концы кривой будут направлены вниз.

Решение задач

Решение практических заданий лучше всего помогает закрепить полученные знания. Существуют физические сборники, которые интересны тем, что включают в себя различные примеры, приближенные к реалистичным задачам. Прорешивая их самостоятельно, ученик не только лучше разберётся в теме, но и научится применять полученные знания на практике.

Вот два таких задания:

Таким образом, чтобы успешно решать задачи, нужно знать несколько основных формул для определения местоположения тела, а также то, как выглядят уравнения параболы и прямой.

Стоит отметить, что существующие онлайн-калькуляторы не умеют вычислять формулы, описывающие траекторию пути. Но вместе с тем их можно использовать для выполнения расчётов или как справочники.

Источник

Начальное положение точки r 30 чему

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

1.1. Даны уравнения движения точки.

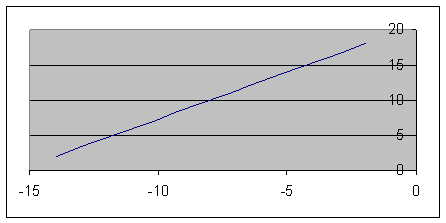
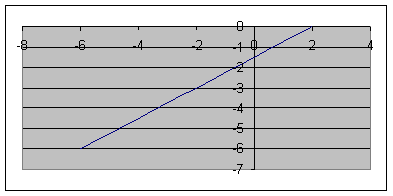
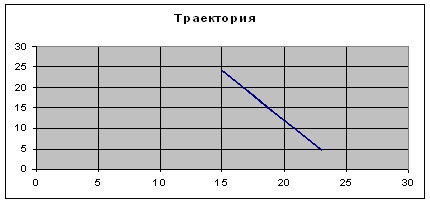
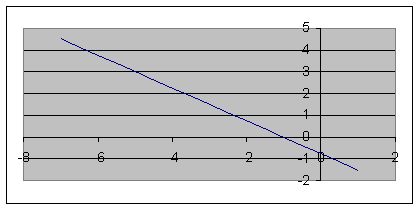
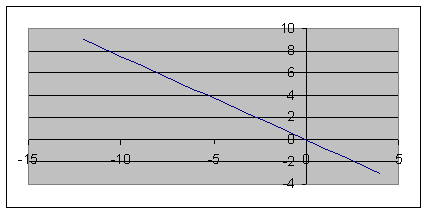
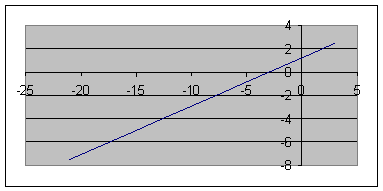
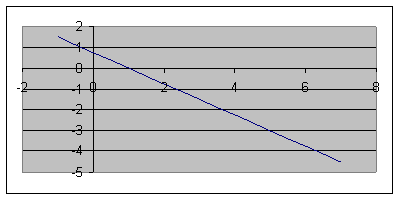
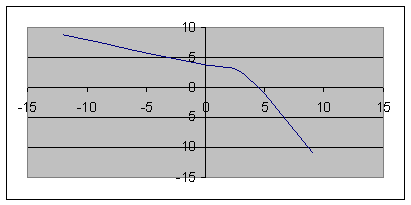
1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

5. Построить график движения точки.

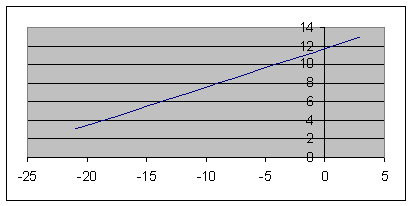
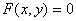
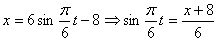
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

Строим уравнение траектории:

2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

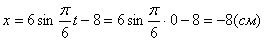
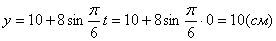
4. Для определения закона движения точки по траектории воспользуемся формулой:

видим, что с выходом из начального положения координата х увеличивается, а координата y увеличивается. Это направление примем за положительное, тогда:

1.2. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 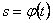, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .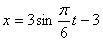

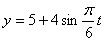
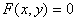
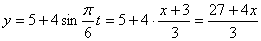
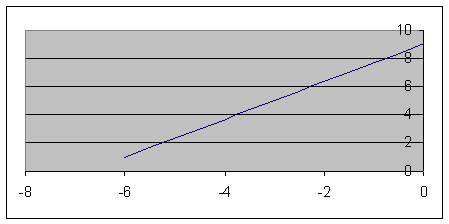
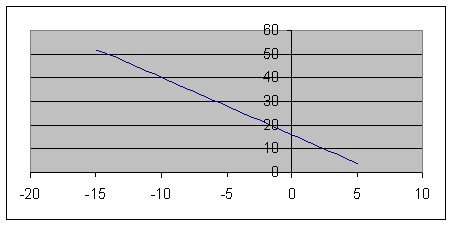
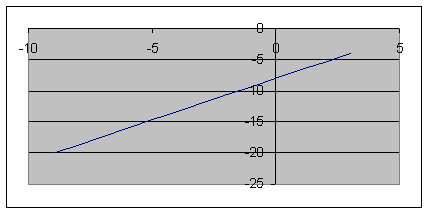
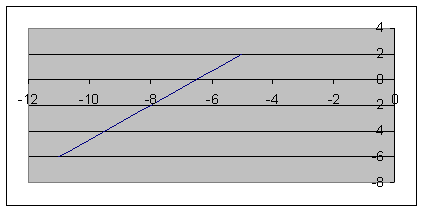
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

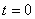
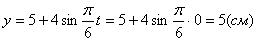
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

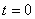
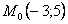
Точка при занимает положение .

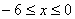
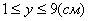
3. Так как x может принимать значения , а y , Пересечение с осью OX в точке (0;9).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

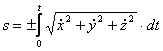
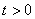
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

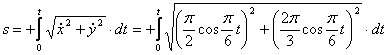
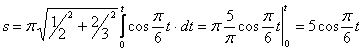
1.3. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

5. Построить график движения точки.

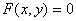
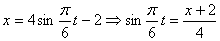
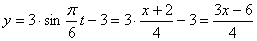
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

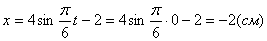
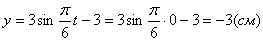
4. Для определения закона движения точки по траектории воспользуемся формулой:

видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

1.4. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

5. Построить график движения точки.

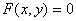
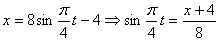
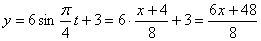
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

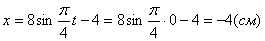
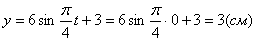
4. Для определения закона движения точки по траектории воспользуемся формулой:

видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

1.5. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

5. Построить график движения точки.

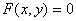
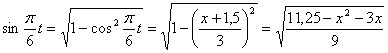
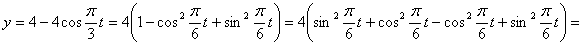
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

Строим уравнение траектории:

2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

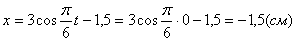
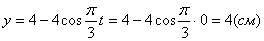
4. Для определения закона движения точки по траектории воспользуемся формулой:

видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

1.6. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

5. Построить график движения точки.

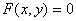
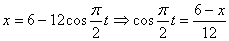
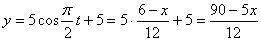
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

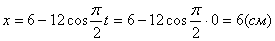
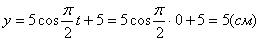
4. Для определения закона движения точки по траектории воспользуемся формулой:

видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

1.7. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

5. Построить график движения точки.

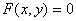
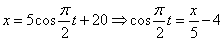
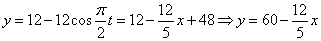
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

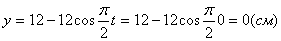
1.8. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 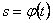, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .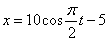

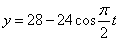
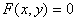
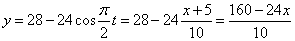
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

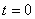
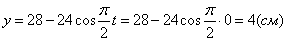
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

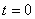
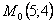
Точка при занимает положение .

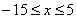
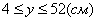
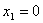
3. Так как x может принимать значения , а y , траектория пересекает ось ОХ при ,

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

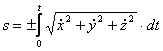
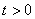
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

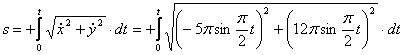
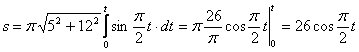
1.9. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

5. Построить график движения точки.

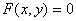
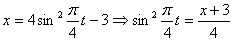
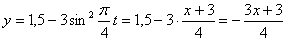
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

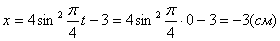
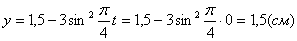
4. Для определения закона движения точки по траектории воспользуемся формулой:

видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

1.10. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 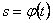, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .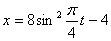

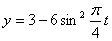
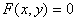
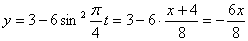
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

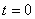
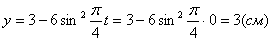
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

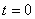
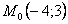
Точка при занимает положение .

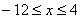
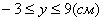
3. Так как x может принимать значения , а y , Пересечение с осями в точке (0;0).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

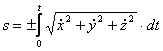
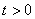
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

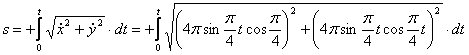
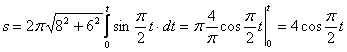
1.11. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 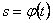, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .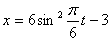

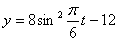
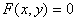
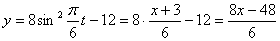
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

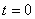
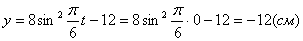
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

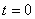
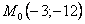
Точка при занимает положение .

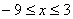
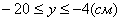
3. Так как x может принимать значения , а y , Пересечение с осями в точке (0;0).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

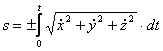
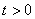
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

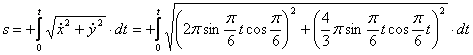
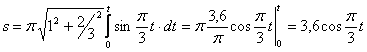
1.12. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 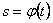, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .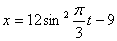

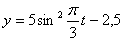
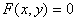
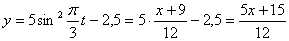
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

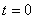
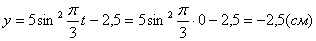
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

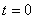
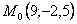
Точка при занимает положение .

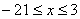
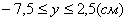
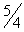
3. Так как x может принимать значения , а y , Пересечение с осью OX в точке (0; ) и пересечение с осью OY (-3;0).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

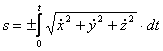
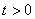
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

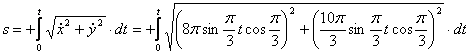
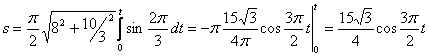
1.13. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 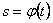, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .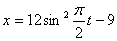

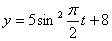
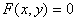
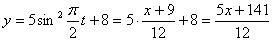
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

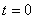
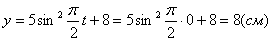
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

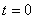
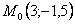
Точка при занимает положение .

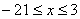
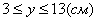
3. Так как x может принимать значения , а y , Пересечение с осью OY в точке (0;11,75).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

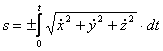
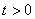
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

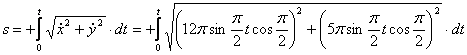
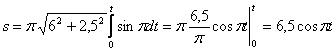
1.14. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 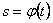, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .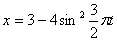

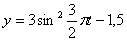
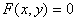
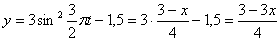
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

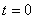
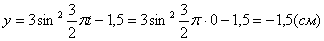
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

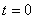
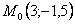
Точка при занимает положение .

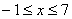
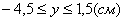
3. Так как x может принимать значения , а y , Пересечение с осью OX в точке (0;0,75) и пересечение с осью OY (1;0).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

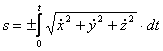
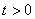
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

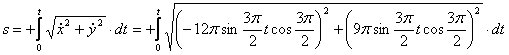
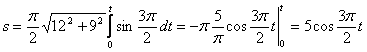
1.15. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 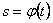, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .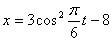

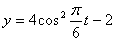
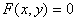
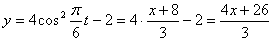
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

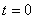
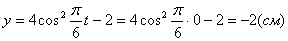
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

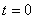
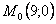
Точка при занимает положение .

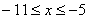
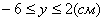
3. Так как x может принимать значения , а y , Пересечение с осью OX в точке (0;-6,5).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

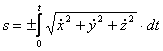
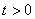
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

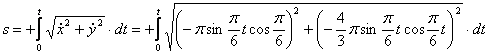
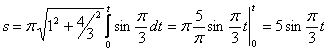
1.16. Даны уравнения движения точки.

1. Определить уравнение траектории и построить ее.

2. Определить начальное положение точки на траектории.

3. Указать моменты времени, когда точка пересекает оси координат.

4. Найти закон движения точки по траектории 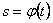, принимая за начало отсчета расстояний начальное положение точки.

5. Построить график движения точки.

Дано: , .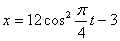

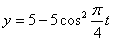
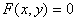
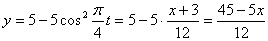
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :

.

Строим уравнение траектории:

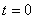
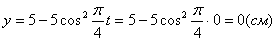
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:

.

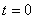
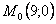
Точка при занимает положение .

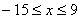
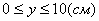
3. Так как x может принимать значения , а y , Пересечение с осью OX в точке (0;3,75) и пересечение с осью OY (9;0).

4. Для определения закона движения точки по траектории воспользуемся формулой:

, при ,

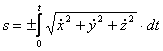
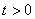
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:

,

.

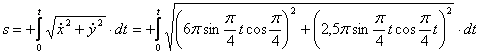
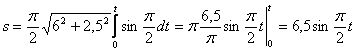
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Источник