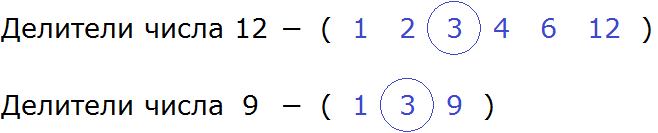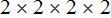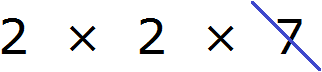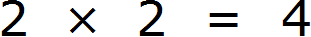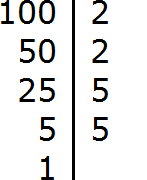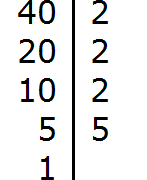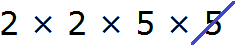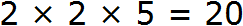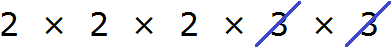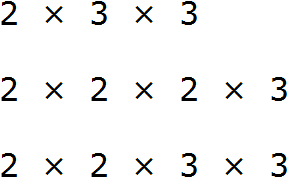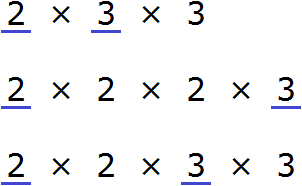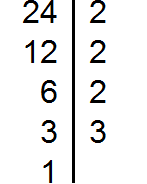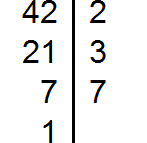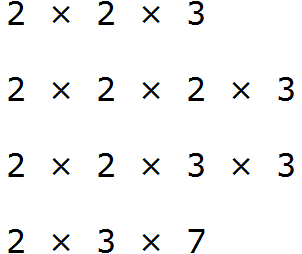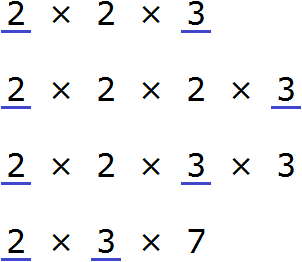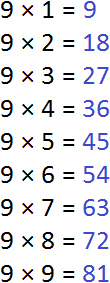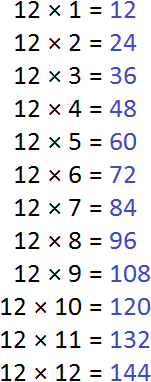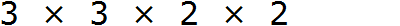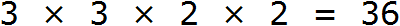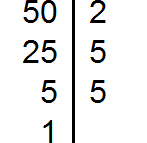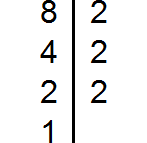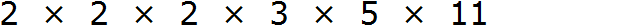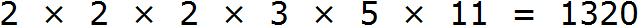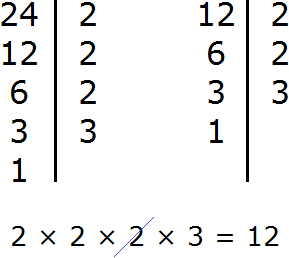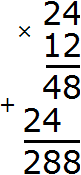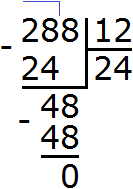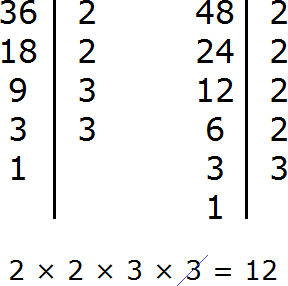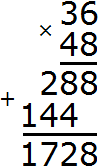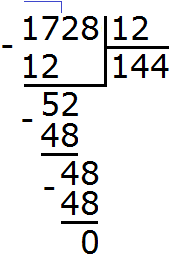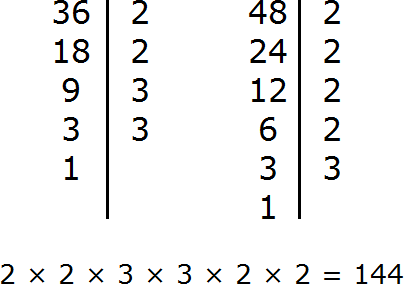Наибольший общий делитель это что в математике

Наибольший общий делитель

Если натуральное число делится только на 1 и на само себя, то оно называется простым.

Любое натуральное число всегда делится на 1 и на само себя.

Число 2 — наименьшее простое число. Это единственное чётное простое число, остальные простые числа — нечётные.

Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.

Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12 ) называются делителями числа.

Делитель натурального числа a — это такое натуральное число, которое делит данное число « a » без остатка.

Натуральное число, которое имеет более двух делителей называется составным.

Общий делитель двух данных чисел « a » и « b » — это число, на которое делятся без остатка оба данных числа « a » и « b ».

Наибольший общий делитель (НОД) двух данных чисел « a » и « b » — это наибольшее число, на которое оба числа « a » и « b » делятся без остатка.

Кратко наибольший общий делитель чисел « a » и « b » записывают так:

Делители чисел в записи решения обозначают большой буквой «Д».

Как найти наибольший общий делитель

Чтобы найти НОД двух или более натуральных чисел нужно:

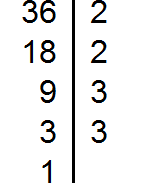
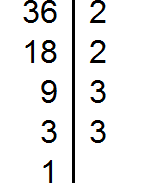
Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных.

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД

НОД (48; 36) = 2 · 2 · 3 = 12

Второй способ записи НОД

На нашем информационном сайте вы также можете с помощью программы помощника найти наибольший общий делитель онлайн, чтобы проверить свои вычисления.

Источник

Наибольший общий делитель (НОД), свойства и формулы

Понятие наибольшего общего делителя

Для начала разберемся, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.

Делитель натурального числа — это такое целое натуральное число, на которое делится данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.

Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общими делителями будут 4 и 1. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4.

Любое число можно разделить на 1 и на само себя. Значит, у любого набора целых чисел будет как минимум два общих делителя.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).

Например, для 4 и 16 НОД будет 4. Как мы к этому пришли:

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, 18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, 18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.

Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.

Еще один пример. Рассчитаем НОД для 28 и 64.

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Способы нахождения наибольшего общего делителя

Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.

1. Разложение на множители

Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.

Пример 1. Найти НОД (84, 90).

Ответ: НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Ответ: НОД (15, 28) = 1.

Пример 3. Найти НОД для 24 и 18.

Ответ: НОД (24, 18) = 6

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

2. Алгоритм Евклида

Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.

Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Пример 1. Найти НОД для 24 и 8.

Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.

В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:

Пример 2. Найти наибольший общий делитель чисел 140 и 96:

Последний делитель равен 4 — это значит: НОД (140, 96) = 4.

Ответ: НОД (140, 96) = 4

Пошаговое деление можно записать столбиком:

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:

Свойства наибольшего общего делителя

У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.

Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.

Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.

Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.

Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.

Доказательство

Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.

Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.

В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.

Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.

Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.

Доказательство

Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.

Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.

Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).

Доказательство

Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.

Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.

Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.

Источник

НОД и НОК

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

Значит НОД (12 и 9) = 3

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

Значит НОД (24 и 18) = 6

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения: 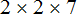и

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

Пример 3. Найти НОД чисел 72 и 128

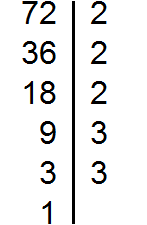
Раскладываем на множители число 72

Раскладываем на множители число 128

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18, 24 и 36

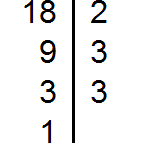
Разложим на множители число 18

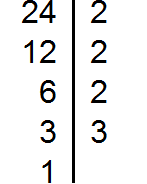
Разложим на множители число 24

Разложим на множители число 36

Получили три разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

Разложим на множители число 12

Разложим на множители число 24

Разложим на множители число 36

Разложим на множители число 42

Получили четыре разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

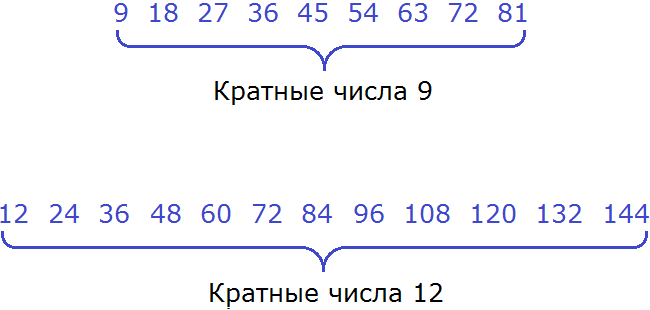
Теперь выпишем кратные обоих чисел:

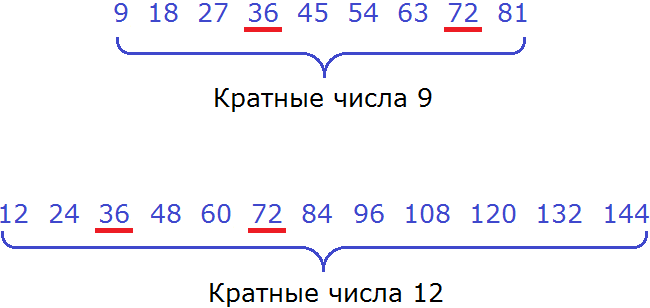
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

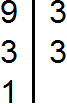
Разложим на множители число 9

Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

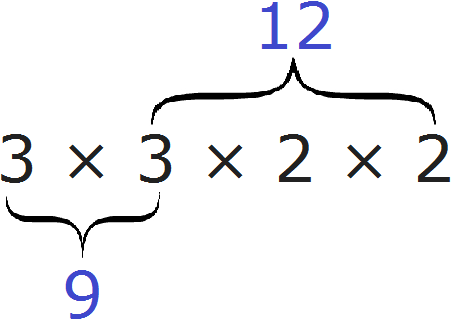
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

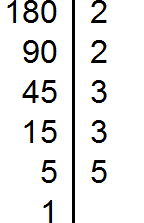
Разложим на множители число 180

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

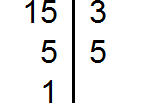
Разложим на множители число 15

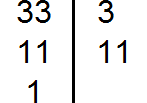
Разложим на множители число 33

Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

НОК (8, 15 и 33) = 1320

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

Разделим полученное число 288 на НОД чисел 24 и 12

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

Перемножим числа 36 и 48

Разделим 1728 на НОД чисел 36 и 48

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».

Источник