Наименьшее общее кратное что это
Как найти наименьшее общее кратное, НОК для двух и более чисел
Школьникам задают немало заданий по математике. Среди них очень часто встречаются задачи с такой формулировкой: имеются два значения. Как найти наименьшее общее кратное для заданных чисел? Необходимо уметь выполнять такие задания, поскольку полученные навыки применяют для работы с дробями при разных знаменателях. В статье разберем, как найти НОК и основные понятия.
Основные понятия
Прежде чем найти ответ на вопрос как находить НОК, нужно определиться с термином кратное. Чаще всего формулировка этого понятия звучит следующим образом: кратным некоторому значению А называют такое натуральное число, которое без остатка будет делиться на А. Так, для 4 кратными будут 8, 12, 16, 20 и так далее, до необходимого предела.
При этом количество делителей для конкретного значения может быть ограниченным, а кратных бесконечно много. Также есть такая же величина для натуральных значений. Это такой показатель, которое делится на них без остатка. Разобравшись с понятием самого меньшего значения для определенных показателей, перейдем к тому, как его находить.
Находим НОК
Наименьшее кратное двух или больше показателей является наименьшим натуральным числом, которое целиком делится на все указанные числа.
Существует несколько способов найти такое значение, рассмотрим следующие способы:
Теперь мы знаем, какова общая методика нахождения самого небольшого значения для двух, трех и более значений. Однако есть и частные методы, помогающие искать НОК, если предыдущие не помогают.
Как находить НОД и НОК.
Частные способы нахождения
Как и для любого математического раздела, имеются частные случаи нахождения НОК, которые помогают в специфических ситуациях:
Частные случаи встречаются реже, нежели стандартные примеры. Но благодаря им можно научиться работать с дробями различной степени сложности. Особенно это актуально для дробей, где имеются неодинаковые знаменатели.
Немного примеров
Разберем несколько примеров, благодаря которым можно понять принцип нахождения наименьшего кратного:
Благодаря примерам можно понять, как находится НОК, какие есть нюансы и в чем заключается смысл таких манипуляций.
Находит НОК гораздо проще, чем может показаться изначально. Для этого применяется как простое разложение, так и умножение простых значений друг на друга. Умение работать с данным разделом математики помогает при дальнейшем изучении математических тем, в особенности дробей разной степени сложности.
Не забывайте периодически решать примеры различными методами, это развивает логический аппарат и позволяет запомнить многочисленные термины. Изучайте методы нахождения такого показателя и вы сможете хорошо работать с остальными математическими разделами. Удачного изучения математики!
Видео
Это видео поможет вам понять и запомнить, как находить наименьшее общее кратное.
Математика. 5 класс
Конспект урока
Наименьшее общее кратное (НОК)
Перечень рассматриваемых вопросов:
– разложение на простые множители;
Кратное число – это число, делящееся на данное целое число без остатка.
Простое число – это такое натуральное число, которое больше 1 и делится только на 1 и само на себя.
Составные числа – это непростые натуральные числа, большие 1.
Взаимно простые числа – это числа, которые не имеют общих простых делителей
Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Ранее мы узнали, что такое кратное, ввели понятие делителя, научились находить наибольший общий делитель, а можно ли каким-либо способом найти общее кратное нескольких чисел? Оказывается, можно, этим сегодня мы и будем заниматься. Но находить не просто общее кратное нескольких чисел, а их наименьшее общее кратное – НОК.
Итак, для начала вспомним, что называется кратным. Это число, делящееся на данное натуральное число без остатка.
Теперь найдём, например, общие кратные чисел 12 и 15. Для этого выпишем все кратные чисел 12 и 15.
12 – его кратные 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …
15 – его кратные 15, 30, 45, 60, 75, 90, 105, 120, 135, …
Из представленных чисел общие кратные – это числа 60 и 120. Меньшее из них – 60. Это и есть наименьшее общее кратное чисел.
Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.
Для нахождения наименьшего общего кратного двух чисел можно использовать несколько способов. Один из них мы рассмотрели на примере нахождения НОК 12 и 15. Этот способ заключается в том, что выписываются все кратные двух чисел и затем находится наименьший общий из них.
Узнаем ещё одно правило нахождения НОК.
Во-первых, разложим числа на простые множители. Далее подчеркнём одинаковые множители этих чисел. Затем перемножим общие множители одного из чисел и добавим произведение всех остальных множителей от каждого числа. Это и будет НОК заданных чисел.
Найдём НОК (15; 16). Разложим числа на простые множители:
Видно, что из всех множителей общий лишь единица, значит, это взаимно простые числа.
НОК взаимно простых чисел – это произведение всех их множителей или произведение этих чисел.
В данном случае НОК равен 240.
Т. е. НОК любых двух простых чисел или двух соседних натуральных чисел будет равен произведению этих чисел.
Найдём НОК (10; 100). Разложим числа на простые множители:
Выделим общие делители у этих чисел, это 2 и 5.
Умножим их, а результат умножим ещё на оставшиеся простые множители от чисел 100 и 10.
НОК (10; 100) = 2 · 5 · 2 · 5 = 100
Обратите внимание на то, что 100 делится нацело на 10, и НОК тоже равен 100. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОК этих чисел равен большему из них.
Некоторые задачи можно решить при помощи НОК проще, чем каким-либо другим способом. Например, рассмотрим такую задачу.
Решение: чтобы решить эту задачу, нужно найти НОК (5;38).
Разложим числа на множители:
Мы видим, что НОК (5; 38) = 5 · 38 = 190 – это будет сумма покупки за шоколад.
Теперь найдём, сколько девочка купит плиток.
Для этого сумму покупки разделим на стоимость одной плитки шоколада.
190 : 38 руб. = 5 – наименьшее количество плиток шоколада, которые сможет купить девочка.
№ 1. Какую цифру нужно подставить в число НОК (7; 2_) вместо пропуска, чтобы получить НОК = 21?
Варианты ответов: 1; 2; 3.
Решение: для решения этой задачи, надо разложить на множители оба числа, при этом вместо пропуска нужно подставить по порядку все цифры. А далее найти подходящий НОК этих чисел, равный 21.
Из всех разложений на множители под НОК (7; 2_) = 21 подходит только число 21.
Ответ: искомая цифра – 1.
№ 2. Какой наименьшей длины должен быть рулон ткани, чтобы от него без остатка можно было отрезать куски по 3 м и 7 м?
Решение: чтобы решить эту задачу, нужно найти НОК заданных чисел, он и будет являться искомым ответом, т. е. наименьшей длиной рулона ткани.
Наименьшее общее кратное НОК.
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
— число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
— число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 – тоже их общие кратные. Среди всех jбщих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим общим кратным (НОК).
НОК всегда натуральное число, которое должно быть больше самого большого из чисел, для которых оно определяется.
Наименьшее общее кратное (НОК). Свойства.
— Коммутативность:
— Ассоциативность:
— Связь с наибольшим общим делителем gcd(a,b):
— В частности, если 

— 
— Наименьшее общее кратное двух целых чисел m и n является делителем всех других общих кратных m и n. Более того, множество общих кратных m, n совпадает с множеством кратных для НОК(m, n).
— Асимптотики для 
Так, функция Чебышёва 
— 
Это следует из определения и свойств функции Ландау g(n).
— 
Нахождение наименьшего общего кратного (НОК).
НОК(a, b) можно вычислить несколькими способами:
1. Если известен наибольший общий делитель, можно использовать его связь с НОК:
2. Пусть известно каноническое разложение обоих чисел на простые множители:
где p1. pk — различные простые числа, а d1. dk и e1. ek — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении).
Тогда НОК (a,b) вычисляется по формуле:
Другими словами, разложение НОК содержит все простые множители, входящие хотя бы в одно из разложений чисел a, b, причём из двух показателей степени этого множителя берётся наибольший.
Вычисление наименьшего общего кратного нескольких чисел может быть сведено к нескольким последовательным вычислениям НОК от двух чисел:
Правило. Чтобы найти НОК ряда чисел, нужно:
— разложить числа на простые множители;
— перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;
— полученное произведение простых множителей будет НОК заданных чисел.
Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.
Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка. Это наименьшее произведение из возможных (150, 250, 300. ), которому кратны все заданные числа.
Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.
Правило. Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.
Чтобы найти наименьшее общее кратное (НОК) нескольких чисел нужно:
1) представить каждое число как произведение его простых множителей, например:
2) записать степени всех простых множителей:
3) выписать все простые делители (множители) каждого из этих чисел;
4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;
5) перемножить эти степени.
Выписываем наибольшие степени всех простых делителей и перемножаем их:
Наименьшее общее кратное
Наиме́ньшее о́бщее кра́тное (НОК) двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n без остатка. Обозначается одним из следующих способов:
Пример: НОК(16, 20) = 80.
Наименьшее общее кратное для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.
Содержание
Свойства
Нахождение НОК
НОК(a, b) можно вычислить несколькими способами.
1. Если известен наибольший общий делитель, можно использовать его связь с НОК:
2. Пусть известно каноническое разложение обоих чисел на простые множители:

где 


Другими словами, разложение НОК содержит все простые множители, входящие хотя бы в одно из разложений чисел a, b, причём из двух показателей степени этого множителя берётся наибольший. Пример:



Вычисление наименьшего общего кратного нескольких чисел может быть сведено к нескольким последовательным вычислениям НОК от двух чисел:
Базовые понятия
Для вычисления НОК (наименьшее общее кратное) необходимо разобраться с терминами и определениями. Если любое натуральное число делится на Х без остатка, это число считается кратным Х. Например, 14, 49, 63 кратны 7.
Любое число в математике может иметь бесконечное множество кратных. А вот количество делителей для него самого ограничено. У простых чисел их всего 2 — это единица и само простое число.
НОК может быть общим сразу для нескольких величин. Если какая-то из них делится без остатка сразу на 2 числа, она называется общим кратным этой пары. Например, 10 кратно одновременно 2 и 5, то есть его можно разделить нацело на 2 и на 5. Однако для 2 и 5 кратным может быть не только 10, но и другие величины — 20, 50, 100 и так далее. С математической точки зрения, важно определить меньшую из этих величин.
Наименьшее общее кратное или НОК для величин А и В — это самое маленькое число, которое одновременно делится на А и на В. То есть оно кратно сразу А и В.
Вместо переменных можно подставлять любые числа и искать для них этот показатель.
Методы нахождения
Чтобы найти НОК 2 чисел, в математике используются три способа. Каждый из них может быть применен для проведения вычислений. Если все операции совершены правильно, в результате получится один и тот же ответ при всех методах.
Первый способ
При этом способе применяется метод простого подбора. Для многих учеников он самый простой. Порядок вычисления будет такой:
Пример: необходимо найти НОК для 6 и 8. Сначала составляется ряд кратных 6. Он будет выглядеть так: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 и так далее. Для числа 8 ряд кратных будет иметь вид: 8, 16, 24, 32, 40. 48, 56, 64, 72, 80 и так далее. Если изучить оба ряда, можно обнаружить 2 одинаковых числа — 24 и 48. Меньшим из них является 24. Это и есть НОК для 6 и 8. Для проверки делят 24 на эти величины. В обоих случаях получаются целые величины без остатка.
Второй вариант
Для вычисления вторым способом нужно разложить на простые множители обе величины. Простым множителем в математике принято называть число, которое делится без остатка только на 1 и на себя.
Следующий шаг — выписываются все множители из первого ряда. Затем добавляются те цифры, которых не было в первом ряду, но были во втором. Получится цепочка из нескольких простых чисел. Их необходимо перемножить между собой, в результате чего получится НОК.
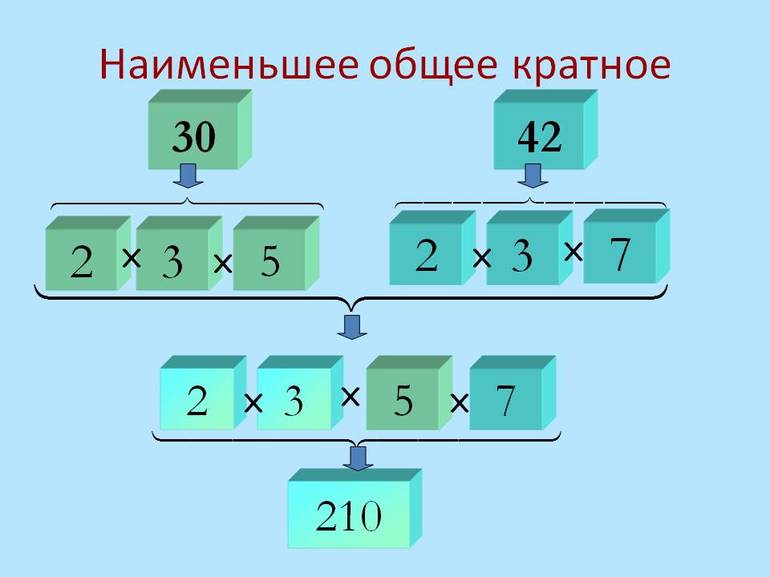
Пример: требуется найти НОК для 8 и 12. Для начала нужно разложить на простые множители 8. Получится 2, 2 и 2. Дальше раскладывается аналогичным образом число 12. Получается 2, 2 и 3. Выписываются множители из первого разложенного ряда 2х2х2. Далее добавляются цифры из второго ряда, которых нет в первом — 2х2х2х3.
После перемножения этих величин получается 24. Это и будет НОК для 12 и 8, поскольку оно делится нацело на оба числа. Фактически все действие сводится к разложению на простые множители двух величин одновременно.
Третий алгоритм
Существует еще один метод нахождения НОК. Решать примеры с его помощью можно только для двух чисел. Необходимо заранее знать наибольший общий делитель — НОД. Так принято называть самое большое число, на которое 2 какие-либо переменные делятся без остатка. Вместо переменных можно ввести конкретные данные. НОД возможно вычислить не только для 2, но и для большего количества величин. В математике это понятие принято записывать кратко НОД (х, у).
Пример: требуется рассчитать НОД для 90 и 117. При разложении на простые множители 90 получается ряд 2,3,3,5. Ту же операцию проводят с числом 117 — получается 3,3,13. Для вычисления НОД умножают общие для двух рядов множители — 3х3=9. Значит, НОД (90,117) = 9.
Часто получается, что наибольший общий делитель равняется одному из чисел. Так бывает, если на него можно разделить все остальные. Например, для 10, 20 и 30 наибольшим делителем будет 10.
Если в задаче необходимо найти одновременно НОД и НОК, применяют третий способ вычисления. Алгоритм работы следующий:
Пример: требуется найти НОД и НОК для чисел 115 и 175. Вначале вычисляется НОД. В этом случае он будет равняться 5. Затем 25 и 40 перемножают, получается 20125.
Полученный результат делят на 5, в итоге НОК 15 и 40 равно 4025.
Чтобы проверить достоверность результата, можно вычислить НОК первым или вторым методами.
Например, нужно найти НОК (25, 40).
Наибольшим делителем для них будет 5. Тогда (25х40):5 = 200.
Проверка вторым способом:
Такой же результат будет получен и при решении вторым методом.
Особые случаи
Не во всех случаях вычисление проводится стандартными способами. Существуют пары чисел с особыми свойствами, для которых найти НОК можно без громоздких вычислений.
К таким случаям относятся следующие:
Большинство учащихся быстро усваивают, как найти НОК двух чисел.
Однако некоторых вводят в растерянность ситуации, когда требуется вычислить НОК или НОД для трех или более исходных. В этом случае необходимо последовательно находить кратное для каждой пары из имеющегося ряда.
Для этих случаев в математике есть особая теорема. Если имеется числовой ряд с формулой А1, А2, А3… Ах, то НОК для всех показателей вычисляется последовательно. Вначале НОК (А1, А2), затем для А2, А3 и так далее.
Однако такой путь может оказаться довольно трудоемким.
Чтобы сэкономить время, можно воспользоваться другим методом поиска:
Применение онлайн-калькулятора
Современные технологии позволяют не рассчитывать нужные данные на бумаге. Любой пользователь может найти в интернете НОД и НОК калькулятор, работающий в онлайн-режиме. Такой онлайн-сервис особенно удобен, если нужно найти делитель и кратное для 3 и более чисел.
Чтобы получить нужные расчеты, достаточно ввести в окошки калькулятора исходные данные и выбрать НОД или НОК. Поскольку между этими понятиями существует тесная связь, обычно они вычисляются вместе. Внизу находится кнопка «найти», которую нужно нажать. Через 2−3 секунды внизу появится ответ. Кроме того, некоторые сервисы выдают не только конечные результаты, но и пошаговый порядок расчетов. Здесь же можно найти онлайн-тесты на заданную тему.
Таким образом, учащийся может понять алгоритм действий и усвоить правило при вычислении НОК онлайн. Это всегда проще сделать на практическом примере.