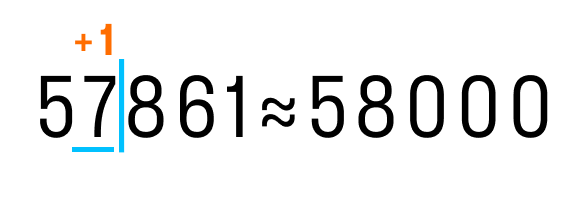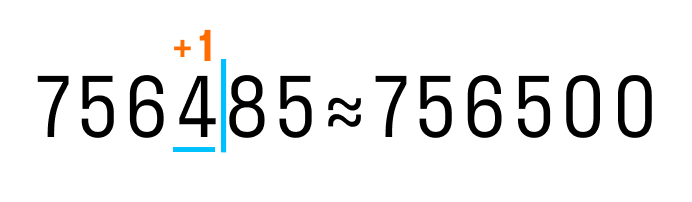Наивысший разряд данного числа что это
Разряды и классы чисел
Классы чисел
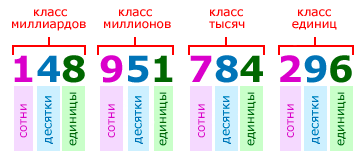
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
Названия классов многозначных чисел справа налево:
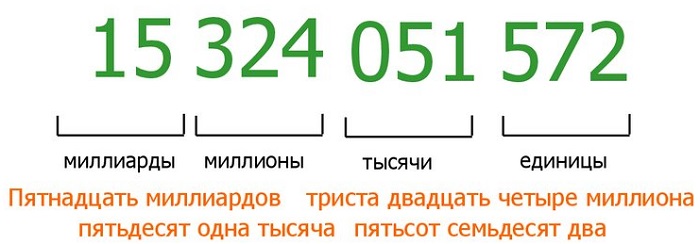
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
Разряды чисел
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
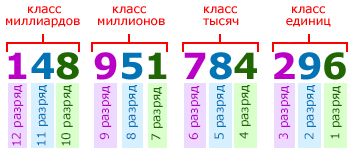
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Пример. Запишите цифрами число, которое содержит:
1) 37 единиц второго класса и 565 единиц первого класса;
2) 450 единиц второго класса и 9 единиц первого класса;
3) 8 единиц второго класса и 50 единиц первого класса.
Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:
| 10 единиц | = | 1 десяток; |
| 10 десятков | = | 1 сотня; |
| 10 сотен | = | 1 тысяча; |
| 10 тысяч | = | 1 десяток тысяч; |
| 10 десятков тысяч | = | 1 сотня тысяч; |
| 10 сотен тысяч | = | 1 тысяча тысяч (1 миллион); |
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра 0 в каком-нибудь разряде означает отсутствие единиц в данном разряде.
Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
24 527 — двадцать четыре тысячи пятьсот двадцать семь.
Классы и разряды
Видеоурок по этой теме можно посмотреть по ссылке: Разряды и классы. Десятичная система счисления.
Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!
Мы выяснили, что в записи натурального числа значение, роль любой цифры зависит от места ее расположения в числе.
Разряд – это позиция, место расположения цифры в записи числа, начиная справа.
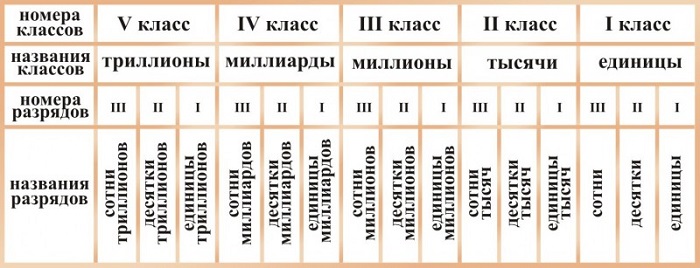
То есть, таблицу 2. в разделе чтение и запись натуральных чисел можно переписать следующим образом:
Таблица 1. Значение разрядов натуральных чисел.
Например, единицы 6-го разряда – это высший разряд по отношению к единицам 3-го разряда, и низшим разрядом по сравнению с единицами 9-го разряда.
Например, в числе 7777 четыре цифры 7, стоящих в разных разрядах, первом, втором, третьем и четвертом.
Если в натуральном числе нет ни одной единицы какого-либо разряда, тогда в этом разряде пишется цифра 0 (нуль).
В начале числа (слева) нули не ставятся.
Число 503 содержит 5 сотен, 0 десятков, 3 единицы.
Любые 10 единиц какого-нибудь разряда создают 1 единицу следующего за ним большего разряда. К примеру, 10 простых единиц создают 1 десяток, 10 сотен создают 1 тысячу.
И наоборот, любая единица высшего разряда включает в себя 10 единиц следующего за ней низшего разряда.
Из таблицы 1 можно заметить, что определенные части в наименовании значений, а именно: единицы, десятки, сотни, повторяются с различными дополнениями, такими как тысячи, миллионы, миллиарды. Например, единицы сотен и единицы миллиардов, сотни миллионов и сотни тысяч и пр.
Класс – это группа разрядов, содержащая в себе три разряда: единицы, десятки и сотни.
Классы, как и разряды, считают справа налево.
При записи многозначного числа можно оставлять небольшой пробел между разными классами, либо разделять их точками. Делается это для удобства чтения натуральных чисел.
Сколько содержится в числе единиц какого-нибудь разряда
Рассмотрим на примере. Допустим, необходимо определить, сколько всего десятков содержит в себе число 28924, то есть, сколько их содержится в десятках тысяч, в тысячах, в сотнях и в десятках данного числа вместе.
Итак, всего число в нашем примере содержит 2000 десятков, да еще 800 десятков, да еще 90 десятков, и еще 2 десятка, то есть, 2892 десятка.
Аналогичным образом можно узнать, что в числе из нашего примера содержится 289 сотен.
Для того, чтобы узнать, сколько всего единиц какого-нибудь разряда содержится в любом числе, необходимо мысленно убрать из него все единицы более низких разрядов, после чего прочитать то число, которое получилось.
Еще один пример: число 54.128.312 содержит: 5.412.831 десятков, 541.283 сотен, 54.128 тысяч, 5.412 десятков тысяч, 541 сотен тысяч, 54 миллиона, 5 десятков миллионов.
Округление чисел
Числа округляют, когда полная точность не нужна или невозможна.
Округлить число до определенной цифры (знака), значит заменить его близким по значению числом с нулями на конце.
Натуральные числа округляют до десятков, сотен, тысяч и т.д. Названия цифр в разрядах натурального числа можно вспомнить в теме натуральные числа.
В зависимости от того, до какого разряда надо округлить число, мы заменяем нулями цифру в разрядах единиц, десятков и т.д.
Если число округляется до десятков, то нулями заменяем цифру в разряде единицы.
Если число округляется до сотен, то цифра ноль должна стоять и в разряде единиц, и в разряде десятков.
Число, полученное при округлении, называют приближённым значением данного числа.
Записывают результат округления после специального знака « ≈ ». Этот знак читается как «приближённо равно».
При округлении натурального числа до какого-либо разряда надо воспользоваться правилами округления.
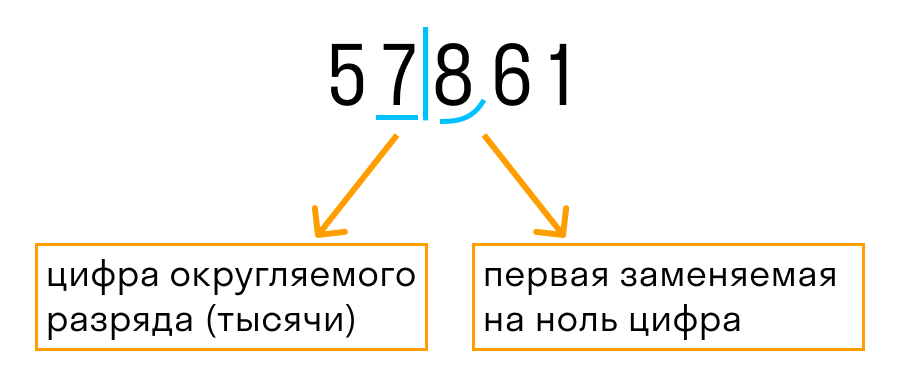
Поясним на примере. Округлим 57 861 до тысяч. Выполним первые два пункта из правил округления.
Теперь округлим 756 485 до сотен.
Округлим 364 до десятков.
Число 360 — приближённое значение с недостатком, а число 370 — приближённое значение с избытком.
В нашем случае, округлив 364 до десятков, мы получили, 360 — приближённое значение с недостатком.
Округлённые результаты часто записывают без нулей, добавляя сокращения «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард).
Округление также применяется для прикидочной проверки ответа в вычислениях.
Пусть нам нужно посчитать:
До точного вычисления сделаем прикидку ответа, округлив множители до наивысшего разряда.
794 · 52 ≈ 800 · 50 ≈ 40 000
Аналогично можно выполнять прикидку округлением и при делении чисел.
Правильное округление чисел
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
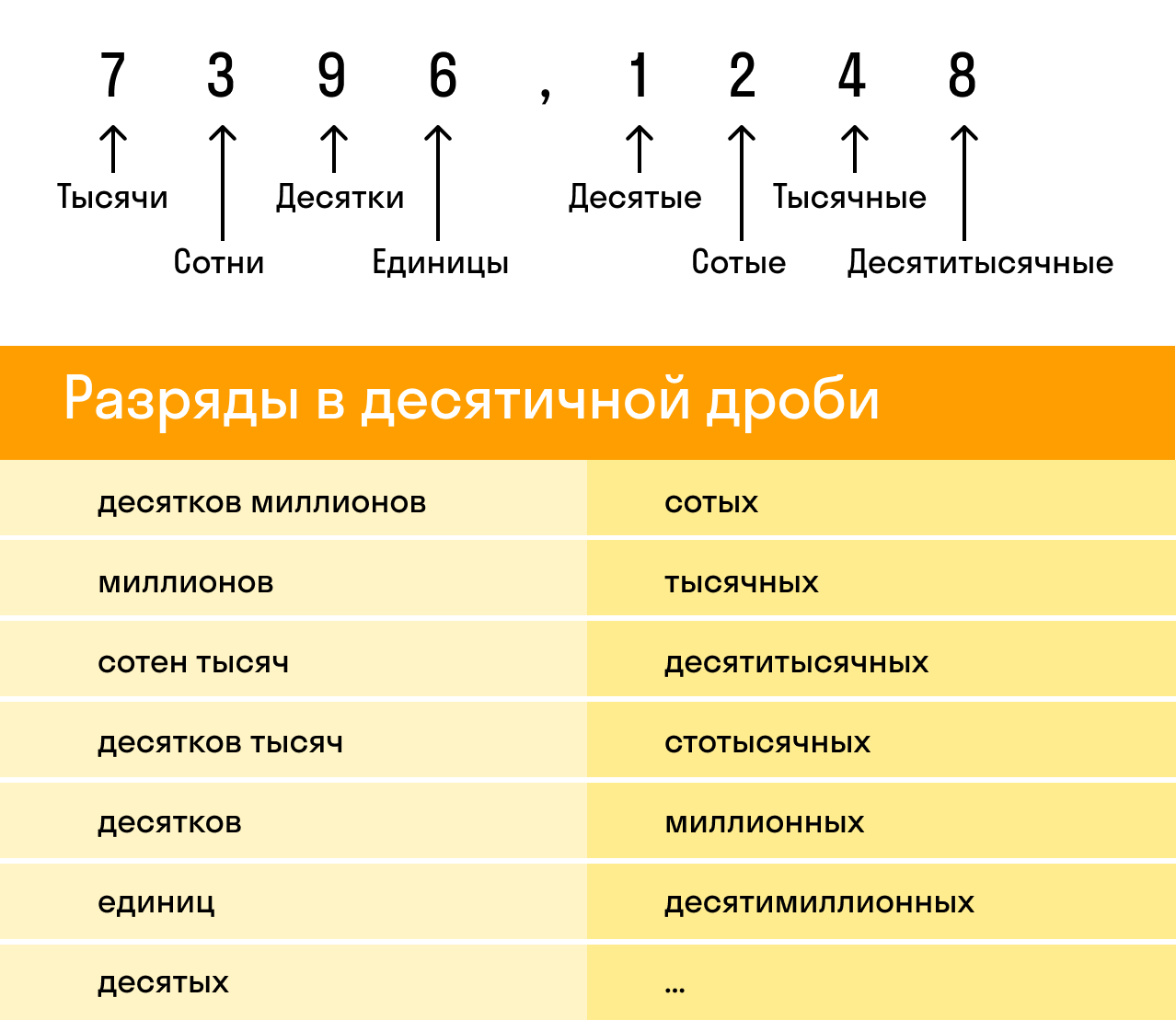
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
Разряды дробной части:
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Разряды чисел – необходимая база для правильного решения примеров любой сложности. Числовые значения являются центральным объектом математики. С ними выполняются все математические действия – от сложения и вычитания до вычисления сложных тригонометрических функций.
Многозначные числа в математике
Прежде чем перейти к основному понятию, требуется вспомнить о натуральных числах – тех, что используются при счете.
Их особенность в том, что они имеют наименьшее значение (1), но не имеют наибольшего или конечного. Ведь счет не имеет конца.
Их можно разделить на группы, в зависимости от того, сколько символов входит в их состав:
Однозначные – если для отображения требуется один символ (1, 2, 3 и т. д.).
Двузначные – когда для записи нужно две цифры (10, 11, 12 и т. д.).
Трехзначные – записывают с помощью трех символов (100, 101, 102 и т. д.).
Перечисление можно продолжать дальше – четырехзначные, пятизначные и т. д. Но для простоты обозначения все числа, содержащие в своей структуре более 1 цифры, называют многозначными.
Разряды чисел
Все натуральные числа записываются с помощью 10 цифр от нуля до девяти. Такая система счисления носит название десятичной.
Кроме того, эта система – позиционная, цифровые символы могут менять положение. Значение каждой следующей позиции больше предыдущей в 10 раз – единицы, десятки, сотни, тысячи и т. д.
Пример 1
Имеются числа 321 и 123. Посмотрим, что они означают, складывая сначала единицы, потом десятки, потом сотни:
321 = 1 * 1 + 2 * 10 + 3 * 100;
123 = 3 * 1 + 2 * 10 + 1 * 100.
Из примера видно, что цифровые символы меняют свое местоположение. Вместе с тем, изменяется числовое значение – в первом случае оно больше.
Место, которое цифра занимает в числе, именуется разрядом. Название каждого элемента соответствует названиям величин счета в десятичной системе. Выделение позиции происходит справа налево, от меньшего к большему.
Важно! Нулем обозначается отсутствие единиц в разрядной позиции. Поэтому он не может стоять на высшей позиции. Например, записывать двадцать три как «023» – некорректно. Правильное написание – 23.
Отнесение цифр к тому или иному месту в числовой записи называется разрядным составом числа.
Пример 2
Разложить на разрядные составляющие число 275.
5 располагается на I разрядной позиции (единицы);
7 – на II разрядном месте десятков;
Классы
Группы разрядов (единица, десяток и сотня) образует классы. Их количество бесконечно.
Чаще всего встречаются следующие:
Как видно, каждый последующий больше предыдущего в 1000 раз.
На письме классы располагаются на небольшом расстоянии друг от друга. Это требуется для более комфортного восприятия написанного.
Например, один миллион двести двенадцать тысяч триста проще прочитать, когда оно записано 1 212 300, а не 1212300.
Пример 3
Классовый разбор числа 56 456 345 выглядит следующим образом:
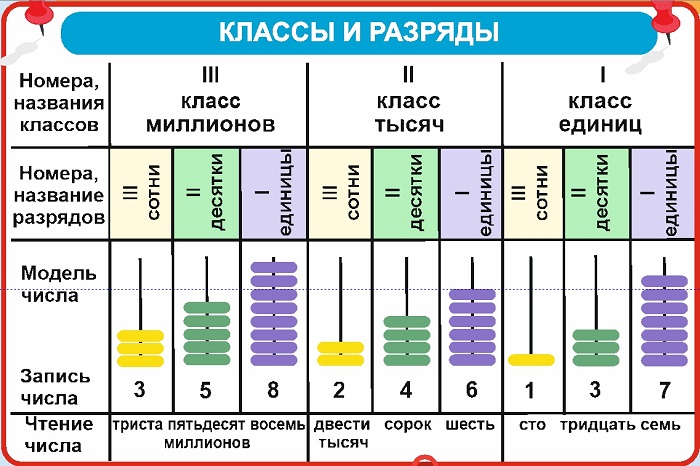
Таблица разрядов и классов цифр
Разрядное и классовое построение легче понять, представив его в виде таблицы: