Наклонная что такое геометрия
Наклонная к прямой
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
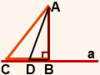
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.
На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
2 Comments
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №10. Перпендикуляр и наклонные
Перечень вопросов, рассматриваемых в теме.
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.
НАКЛОННАЯ
Смотреть что такое «НАКЛОННАЯ» в других словарях:
наклонная — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
наклонная — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Наклонная к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого. * * * НАКЛОННАЯ НАКЛОННАЯ к прямой l, прямая, пересекающая прямую l под углом,… … Энциклопедический словарь
Наклонная — ж. разг. Наклонная плоскость. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Наклонная — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Н. к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого … Большая советская энциклопедия
НАКЛОННАЯ — к прямой I прямая, пересекающая прямую Iпод углом, отличным от прямого. Н. к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого. БСЭ 3 … Математическая энциклопедия
НАКЛОННАЯ — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Н. к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого … Естествознание. Энциклопедический словарь
НАКЛОННАЯ — Характеристика линии или плоскости, которая, пересекав другую линию или плоскость под углом, отличным от угла в 90°. В графически представлениях факторного анализа две оси, представляющие коррелир щие факторы, являются наклонными … Толковый словарь по психологии
наклонная поверхность подошвы рельса — Ндп. наклонная грань подошвы рельса Поверхность, соединяющая шейку рельса с боковой гранью подошвы. Примечания 1. В рельсах типов Р75, Р65, Р50, Р38, Р33, Р24, Р18, P11, Р8 и Р5 наклонная поверхность подошвы выполнена в виде прямой линии под… … Справочник технического переводчика
наклонная орбита — Любая орбита спутника, кроме экваториальных и полярных. Наклонные орбиты бывают эллиптические и круговые, синхронные и несинхронные. Термин “наклонная орбита” применим и к геостационарным спутникам, орбита которых из за нестабильности … Справочник технического переводчика
НАКЛОННАЯ ПЛОСКОСТЬ — НАКЛОННАЯ ПЛОСКОСТЬ, простейшее устройство, представляющее собой плоскость, приподнятую с одного края. Проще толкать груз (массой ) вверх по наклонной плоскости (под углом к горизонтали), чем поднимать его вертикально это дает МЕХАНИЧЕСКИЙ… … Научно-технический энциклопедический словарь
НАКЛОННАЯ
Смотреть что такое «НАКЛОННАЯ» в других словарях:
НАКЛОННАЯ — к прямой l прямая, пересекающая прямую l под углом, отличным от прямого. Наклонная к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого … Большой Энциклопедический словарь
наклонная — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
наклонная — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Наклонная к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого. * * * НАКЛОННАЯ НАКЛОННАЯ к прямой l, прямая, пересекающая прямую l под углом,… … Энциклопедический словарь
Наклонная — ж. разг. Наклонная плоскость. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Наклонная — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Н. к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого … Большая советская энциклопедия
НАКЛОННАЯ — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Н. к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого … Естествознание. Энциклопедический словарь
НАКЛОННАЯ — Характеристика линии или плоскости, которая, пересекав другую линию или плоскость под углом, отличным от угла в 90°. В графически представлениях факторного анализа две оси, представляющие коррелир щие факторы, являются наклонными … Толковый словарь по психологии
наклонная поверхность подошвы рельса — Ндп. наклонная грань подошвы рельса Поверхность, соединяющая шейку рельса с боковой гранью подошвы. Примечания 1. В рельсах типов Р75, Р65, Р50, Р38, Р33, Р24, Р18, P11, Р8 и Р5 наклонная поверхность подошвы выполнена в виде прямой линии под… … Справочник технического переводчика
наклонная орбита — Любая орбита спутника, кроме экваториальных и полярных. Наклонные орбиты бывают эллиптические и круговые, синхронные и несинхронные. Термин “наклонная орбита” применим и к геостационарным спутникам, орбита которых из за нестабильности … Справочник технического переводчика
НАКЛОННАЯ ПЛОСКОСТЬ — НАКЛОННАЯ ПЛОСКОСТЬ, простейшее устройство, представляющее собой плоскость, приподнятую с одного края. Проще толкать груз (массой ) вверх по наклонной плоскости (под углом к горизонтали), чем поднимать его вертикально это дает МЕХАНИЧЕСКИЙ… … Научно-технический энциклопедический словарь
Перпендикуляр и наклонная:
Рассмотрим понятия перпендикуляра и наклонной к прямой в плоскости.
Пусть точка О и прямая а лежат в плоскости, а точка О не лежит на прямой а.
Перпендикуляром, проведенным из точки О к прямой а, называется отрезок ОB, такой, что точка B лежит на прямой а и отрезок ОB перпендикулярен прямой а. Точка B называется основанием перпендикуляра.
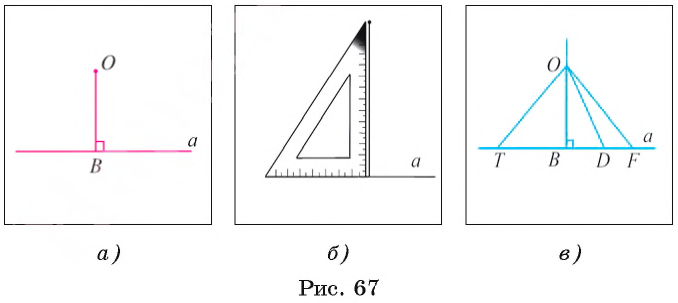
На рисунке 67, а отрезок ОB — перпендикуляр, проведенный из точки О к прямой а.
При изображении перпендикулярных прямых или перпендикуляра пользуются чертежным угольником (рис. 67, б).
Пусть точка B — основание перпендикуляра ОB, проведенного из точки О к прямой а.
Отрезок, соединяющий точку О с любой точкой прямой а, не совпадающей с основанием B перпендикуляра, называется наклонной к прямой а.
На рисунке 67, в изображены наклонные OF, OD и ОТ к прямой а.
Теорема 1 (о существовании единственного перпендикуляра, проведенного из точки к прямой).
Из точки, не лежащей на прямой в плоскости, можно провести единственный перпендикуляр к данной прямой.
1. Докажем, что такой перпендикуляр существует.
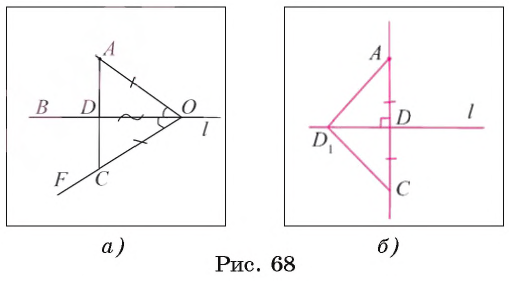
Пусть точка А не принадлежит прямой l. Возьмем на этой прямой некоторую точку О и проведем луч ОА (рис. 68, а). Далее от луча OB в другой полуплоскости отложим угол BOF, равный углу АОВ. На луче OF отложим отрезок ОС, равный отрезку ОА. Пусть точка D — точка пересечения отрезка АС и прямой l. Треугольник AOD равен треугольнику COD по первому признаку равенства треугольников, т. к. АО = ОС, сторона OD — общая, 
2. Докажем единственность перпендикуляра.
Воспользуемся методом доказательства от противного. Предположим, что из точки А можно провести еще один перпендикуляр АD к прямой l. Пусть DС — луч, противоположный лучу DА, и DС = DА (рис. 68, б). Треугольники D1DA и D1DС равны по первому признаку равенства треугольников, так как DС = DА, сторона DD1— общая, ADD1 = CDD1. Следовательно, AD1D = CD1D. Так как по предположению AD1D = 90°, то CD1D = 90°, т. е. угол AD1C развернутый и лучи D1A и D1C составляют прямую. Таким образом, получаем, что через две точки А и С проходят две прямые, что противоречит аксиоме о существовании единственной прямой, проходящей через две точки. Значит, предположение о том, что из точки можно провести два перпендикуляра к прямой, неверно. Следовательно, такой перпендикуляр единственный.
Теорема 2. Если две прямые плоскости перпендикулярны третьей прямой этой плоскости, то они не пересекаются.
Пусть прямые а и b перпендикулярны прямой l. Докажем, что прямые а и b не пересекаются. Допустим, что прямые а и b пересекаются в некоторой точке О. Пусть прямые а и b пересекают прямую l в точках F и D соответственно. Тогда получаем, что из точки О к прямой l проведены два перпендикуляра OF и ОD. Это противоречит теореме о существовании единственного перпендикуляра, проведенного из точки к прямой. Значит, наше предположение о том, что прямые а и b пересекаются, неверно. Прямые а и b не пересекаются.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.