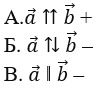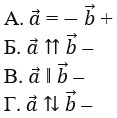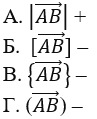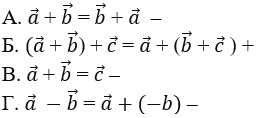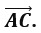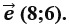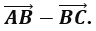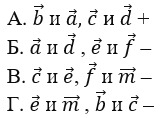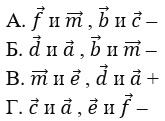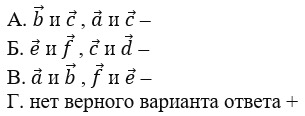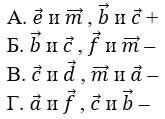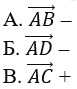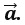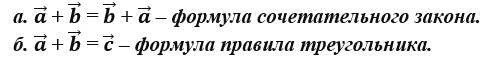Направление и размер это характеристики чего ответ
Направление и размер это характеристики чего ответ
Тесты по геометрии 9 класс. Тема: «Векторы»
Правильный вариант ответа отмечен знаком +
1. Отрезок, для которого указано, какой из его концов является началом, а какой – концом, называется:
Г. нет верного варианта ответа –
2. Любая точка пространства может рассматриваться как вектор. Такой вектор называется:
3. Два ненулевых вектора, лежащие на одной прямой или на параллельных прямых, называются:
В. противоположно направленными –
4. Какие слова пропущены в предложении?
Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково (тогда их называют …), либо противоположно (тогда их называют …).
А. сонаправленные; разнонаправленные –
Б. противоположно направленные: сонаправленные –
В. сонаправленные: противоположно направленные +
Г. нет верного варианта ответа –
5. Длиной ненулевого вектора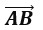 
называется:
Б. длина отрезка AB +
Г. нет верного варианта ответа –
6. Выберите верное обозначение сонаправленных векторов.
Г. нет верного варианта ответа –
7. Векторы называются равными, если:
В. они сонаправлены –
Г. они сонаправлены и их длины равны +
8. Выберите верное обозначение противоположных векторов.
9. Выберите верное обозначение длины вектора
тест 10. 
11. 
– это формула:
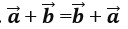
А. разности вектора –
Б. сочетательного закона –
В. нет верного варианта ответа –
Г. переместительного закона +
12. Выберите верную формулу сочетательного закона.
13. Вектор 
отложен от точки M. Точка M является:
А. концом вектора –
Б. началом вектора +
В. серединой вектора –
Г. нет верного варианта ответа –
14. Если длины двух ненулевых векторов равны, и они противоположно направлены, то они называются:
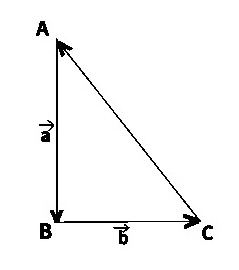
15. ABC – прямоугольный треугольник,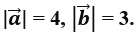 
Найдите длину вектора 
16. 
17. Найдите длину вектора 
18. Дан правильный треугольник ABC со стороной 2. Найдите длину вектора 
Г. недостаточно данных –
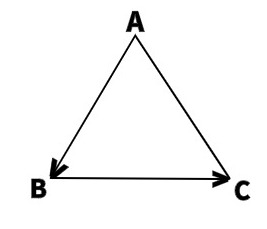
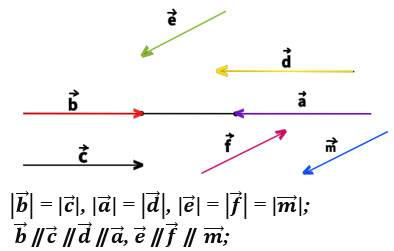
19. Выберите пары противоположно направленных векторов.
тест-20. Выберите пары сонаправленных векторов.
21. Выберите пары противоположных векторов.
22. Выберите пары равных векторов.
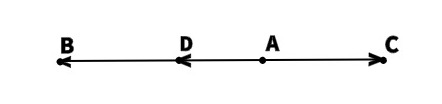
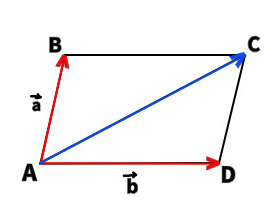
23. Дан параллелограмм ABCD, AC – диагональ Найдите сумму векторов 
Г. нет верного варианта ответа –
24. Выберите верную формулировку правила многоугольника.
А. Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов. +
Б. От любой точки можно отложить вектор, равный данному, и притом только один. –
В. Чтоб сложить два вектора, нужно из произвольной точки отложить один вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало одного с концом второго. –
Г. Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов. –
25. Верны ли следующие суждения?
а. Векторы называются равными, если они коллинеарные и их длины равны.
б. Длиной нулевого вектора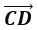 
является длина отрезка CD.
В. оба суждения верны –
Г. оба суждения неверны –
26. Верны ли следующие суждения?
а. Направленный отрезок (вектор), длина которого равна нулю, – это нулевой вектор.
б. От любой точки можно отложить вектор, равным данному, и притом только один.
В. оба суждения верны +
Г. оба суждения неверны –
27. Верны ли следующие суждения?
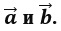
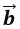
а. Разностью векторов называется такой вектор, сумма которого с вектором 
равна вектору 
б. Два ненулевых вектора называются коллинеарными, если их длины равны и они противоположно направлены.
В. оба суждения верны –
Г. оба суждения неверны –
28. Верны ли следующие суждения?
В. оба суждения верны –
Г. оба суждения неверны –
29. Верны ли следующие суждения?
а. Вектор называется нулевым, если его начальная и конечная точка совпадает.
б. Модулем вектора называется длина вектора, выраженная числовым выражением.
В. оба суждения верны +
Г. оба суждения неверны –
тест_30. Верны ли следующие суждения?
а. Скалярные величины характеризуются числом и направлением, а векторные только числом.
б. К векторным величинам относятся скорость, ускорение, перемещение.
Характеристики вектора: длина, направление, координаты
У любого вектора есть 2 главные характеристики:
Третья характеристика вектора – это его координаты.
Примечание:
Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.
Что такое координаты вектора
Координаты вектора – это длины его теней на осях координат (его проекции на оси).
Координаты вектора указывают так:
\( a_
\( a_
Координаты вектора можно получить из координат его начальной и конечной точек:
«координата вектора» = «конец» — «начало»
Пример:
\( A \left( 1;1 \right) \) — начальная точка,
\( B \left( 4;3 \right) \) — конечная точка,
\[ \overrightarrow
\[ \begin
Длина вектора (в чем измеряется, как посчитать)
Длину вектора (его модуль) обозначают так:
Как вычислить длину вектора по его координатам
Когда известны координаты вектора, его длину считают так:
\( a_
Для двухмерного вектора:
Для трехмерного вектора:
Как вычислить длину вектора с помощью рисунка
Если вектор нарисован на клетчатой бумаге, длину считаем так:
1). Если вектор лежит на линиях клеточек тетради:
— считаем количество клеточек.
Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.
2). Если вектор не лежит вдоль линий:
— проводим вертикаль и горизонталь пунктиром.
\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;
— затем применяем формулу:
Как указать направление вектора
Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.
Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.
Для двумерного вектора
Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:
Словами указать направление вектора можно так:
Такой способ указания координат используют в полярной системе координат.
Для трехмерного вектора
Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.
Такой способ указания координат используют в сферической системе координат.
Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).
Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.
Для указания сферических координат принято использовать:
Электрическое поле и его характеристики
теория по физике 🧲 электростатика
Вокруг заряженных тел существует особая среда — электрическое поле. Именно это поле является посредником в передаче электрического взаимодействия.
Свойства электрического поля
Характеристики электрического поля
Напряженность численно равна электрической силе, действующей на единичный положительный заряд:
q 0 — пробный заряд.
Пример №1. Сила, действующая в поле на заряд в 20 мкКл, равна 4Н. Вычислить напряженность поля в этой точке.
20 мкКл = 20∙10 –6 Кл
Силовые линии — линии, касательные к которым совпадают с вектором напряженности.
Потенциальная энергия взаимодействия двух зарядов W (Дж) в вакууме:
Потенциальная энергия взаимодействия двух зарядов W (Дж) в среде:
Знак потенциальной энергии зависит от знаков заряженных тел:
Потенциал — энергетическая характеристика электрического поля. Обозначается как ϕ. Единица измерения — Вольт (В).
Численно потенциал равен отношению потенциальной энергии взаимодействия двух зарядов к единичному положительному заряду:
q 0 — пробный заряд.
Потенциал — скалярная физическая величина. Знак потенциала зависит от знака заряда, создающего поле. Отрицательный заряд создает отрицательный потенциал, и наоборот.
Значение потенциала зависит от выбора нулевого уровня для отсчета потенциальной энергии, а разность потенциалов — от выбора нулевого уровня не зависит.
Напряжение — разность потенциалов. Обозначается как U. Единица измерения — Вольт (В). Численно напряжение равно отношению работы электрических сил по перемещению заряда из точки 1 в точку 2:
Эквипотенциальные поверхности — поверхности, имеющие одинаковый потенциал. Они равноудалены от заряженных тел и обычно повторяют их форму. Эквипотенциальные поверхности перпендикулярны силовым линиям.
Пылинка, имеющая массу 10 −6 кг, влетела в однородное электрическое поле в направлении против его силовых линий с начальной скоростью 0,3 м/с и переместилась на расстояние 4 см. Каков заряд пылинки, если её скорость уменьшилась при этом на 0,2 м/с, а напряжённость поля 105 В/м?