Напряжение в чем измеряется сопромат нормальное
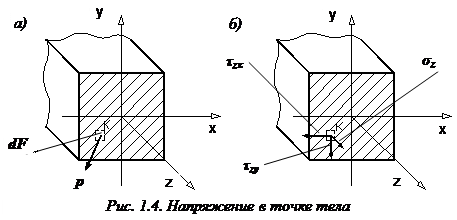
Напряжение в точке тела
Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения.
Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы 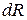
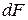
В количественном выражении 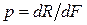
Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K.
Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).
Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( 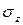
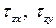
Между полным (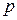
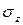
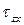
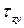
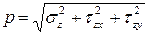
Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.
Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:
1 МПа = 106 Па; 1 кН/см2 = 107 Па.
изучаем сопротивление материалов
Напряжения
Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_
Тензор напряжений
Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений
$$ T _\sigma = \left[\matrix <
\sigma _x & \tau _
\tau _
>\right]$$
Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.
При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.
В каждой точке можно провести три взаимно-перпендикулярных главных площадки.
При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).
Связь внутренних усилий и напряжений
Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.

Выполнив интегрирование по площади поперечного сечения получим:
То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.
1 Проекция вектора полного напряжения на нормаль к данной площадке называется нормальным напряжением и обозначается через σn.
iSopromat.ru
Напряжение в механике — это мера интенсивности распределения внутренних сил R в окрестности точки в пределах данного сечения площадью A.
Таким образом, напряжения p измеряются в единицах силы, отнесенной к единице площади dA

Единица измерения напряжений — Паскаль (Н/м 2 =Па).
Рассмотрим подробнее:
Система приложенных к телу внешних нагрузок, приводит к возникновению в его сечениях внутренней силы R и момента M
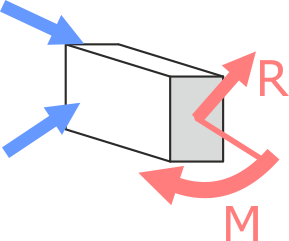
При этом надо понимать что внутренняя сила и внутренний момент воздействуют на всё сечение бруса в целом.
Выделим в рассматриваемом сечении элементарную площадку dA бесконечно малой площади.
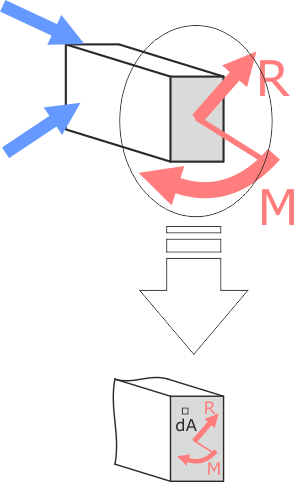
Полное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.
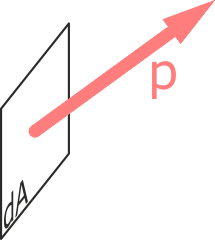
Обозначение полного напряжения в точке – p.
Единица измерения – Паскаль [Па] (Н/м 2 ).
Ввиду того, что большинство конструкционных материалов обладает высокой прочностью часто напряжения, возникающие в них, измеряются в кратных величинах, например мегапаскаль [МПа].
В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):
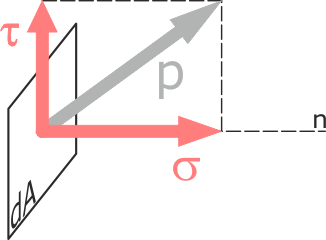
Проекция вектора полного напряжения p на нормаль к сечению называется нормальным напряжением и обозначается через σ, а проекция вектора полного напряжения на плоскость сечения называется касательным напряжением и обозначается через τ.
Разложение вектора полного напряжения на две указанные составляющие имеет конкретный физический смысл – с нормальным напряжением связано разрушение путем отрыва, а с касательным – разрушение путем сдвига или среза.
В частных случаях (например при растяжении-сжатии и кручении) в поперечных сечениях бруса имеют место только нормальные и только касательные напряжения соответственно.
При решении таких задач, величина нормальных и касательных напряжений сравнивается с соответствующими допустимыми значениями напряжений.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Напряжения

Рис. 3.1. Среднее напряжение на площадке

Величина p называется истинным напряжением или просто напряжением в данной точке данного сечения.
Напряжения, как и силы, являются векторными величинами. В каждой точке сечения тела полное напряжение p можно разложить на две составляющие (рис. 3.2):
1) составляющую, нормальную к плоскости сечения. Эта составляющая называется нормальным напряжением и обозначается σ ;
Рис. 3.2. Разложение вектора полного напряжения
Вычислим сумму моментов всех элементарных сил, действующих на элемент (рис.3.3), относительно координатных осей, так, например, для оси x с учетом равновесия элемента, имеем:

Повторяя указанные действия для других осей, получим закон парности касательных напряжений :

ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Нормальные напряжения при изгибе
При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит название чистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу.

Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называется нейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки. Нейтральная линия — это линия, в которой нормальные напряжения равны нулю.
Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе.
Допущения для вывода формул нормального напряжения: 1) Выполняется гипотеза плоских сечений. 2) Продольные волокна друг на друга не давят (гипотеза о ненадавливании) и, следовательно, каждое из волокон находится в состоянии одноосного растяжения или сжатия. 3) Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми. 4) Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости. 5) Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков. 6) Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.
Рассмотрим балку произвольного сечения, но имеющую ось симметрии.


Формула (1) выражает статическую сторону задачи об изгибе прямого бруса, но по ней по известному изгибающему моменту нельзя определить нормальные напряжения, пока не установлен закон их распределения.
Выделим на среднем участке балки и рассмотрим участок длиной dz, подвергающийся изгибу. Изобразим его в укрупненном масштабе.
К выводу формул при изгибе: а) участок балки до деформации; б) участок балки после деформации



Подставим полученное выражение кривизны (4) в выражение (3) и получим формулу для вычисления нормальных напряжений в любой точке поперечного сечения:
Тогда максимальные напряжения: 
Условие прочности при изгибе:
Нейтральная линия. Вопрос о положении нейтральной линии.
При изгибе отсутствует продольная сила, поэтому можно записать 



Условие 



Установив положение нейтральной линии, несложно построить эпюру нормальных напряжений по высоте сечения. Ее линейный характер определяется уравнением первой степени.
Характер эпюры σ для симметричных сечений относительно нейтральной линии, М Запись опубликована 18.04.2015 автором admin в рубрике Изгиб.