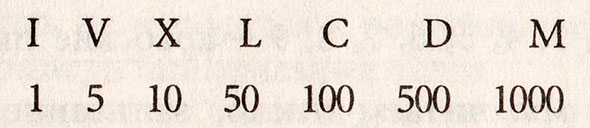Натуральные числа для чего людям понадобились эти числа
Что такое натуральные числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое НАТУРАЛЬНЫЕ ЧИСЛА.
С ними человек встречается с самого рождения. Например, когда считает пальцы на руке – 1, 2, 3, 4, 5. Или отмечает праздники – 8 марта, 23 февраля, 9 мая, 31 декабря.
Натуральные числа — это.
Натуральные числа – это те числа, которые возникают при подсчете чего-либо. Например, одно яблоко, два яблока, пять яблок десять яблок и так далее.
Лучше даже представить, что вы подсчитываете людей, ибо их нельзя поделить на части, как большинство предметов (например, разрезов яблоко пополам).
Само слово «naturalis» в переводе с латинского означает «естественный».
Если число не является ни дробным, ни отрицательным, то его можно назвать натуральным.
Натуральными числами люди пользуются уже много тысячелетий. Просто у разных народов были разные системы исчисления. Например, римляне для счета использовали палочки. Так и появились знаменитые римские цифры – I, V, X, L, C, D и M.
А вот в Древнем Вавилоне использовали шестеричную систему. И до наших дней она дошла в виде часов, в которых 1 час равен 60 минутам, а 1 минута равна 60 секундам.
И наконец, современное обозначение цифр (0, 1, 2, 3, 4, 5 и так далее) принадлежит арабам, хотя за основу они взяли индийскую десятеричную систему и добавили к ней «ноль».
Натуральный ряд
Если расположить натуральные числа в порядке возрастания, то полученная цепочка будет называться натуральным рядом.
Он всегда появляется, когда нам нужно что-то посчитать поштучно. Например, в магазине мы обычно так делаем с овощами или фруктами, берем 5 морковок или 3 яблока. А уже только потом взвешиваем их, так как цены указаны за килограмм.
И конечно, именно так учатся считать школьники в первом классе. Например, если в задачке нарисовано пять флажков и вопрос звучит «сколько?», то любой ребенок будет считать «пальцем», отмечая каждый флажок и озвучивая натуральный ряд «один, два, три, четыре, пять».
Ну и тут же будет важным упомянуть, что количество натуральных чисел бесконечно. А значит, и натуральный ряд является бесконечным.
Это записано в основном законе натуральных чисел:
Каким бы большим не было натуральное число N, всегда найдется натуральное число N+1, которое будет больше.
Ноль — это натуральное число или нет
Натуральный ряд можно построить двумя способами:
Вы спросите, в чем разница? Во втором случае возможен вариант, когда нужного предмета может и не быть вовсе. И тогда его количество равно нулю.
То есть натуральный ряд начинается не с единицы, а с ноля. И выглядит вот так: 0, 1, 2, 3, 4, 5 и так далее.
Соответственно, в первом случае ноль нельзя считать натуральным числом. А во втором – можно. Интересно, что споры, какой подход более правильный, у математиков идут до сих пор. И сторонников обеих теорий примерно поровну.
Но у российских школьников проблем с выбором нет. В нашей стране придерживаются той версии, что ноль – это натуральное число.
Операции с натуральными числами
Школьники в младших классах на уроках математики имеют дело только с натуральными числами. Помимо самих цифр учатся и самым простым действиям:
Вот и все, что мы хотели рассказать о натуральных числах.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
А стоит ли себе забивать голову, какое число натуральное, а какое нет? Мир от этого не станет, ни проще, ни сложнее. Да и что неестественного в отрицательных числах? Если человеку не хватает денег, чтобы рассчитаться с долгами, то его имущество как раз уйдет в минус, отдал за долги всё, что было, но остался должен, значит необходимо ещё заработать, чтоб из минуса выйти в ноль.
Презентация по математике на тему «Натуральные числа в жизни человека»
Описание презентации по отдельным слайдам:
Натуральные числа в жизни человека Работа ученицы 7 класса Европейской школы Тропиковой Ани Руководитель Галдобина О.В.
Натуральные числа в жизни человека Число – одно из основных понятий математики, позволяющее выразить результаты счета или измерения. Понятие числа служит исходным для многих математических теорий. Числа находят широкое применение В физике, механике, астрономии, химии и многих других науках. Числами постоянно пользуются в повседневной жизни.
Натуральные числа в жизни человека При рождение мы сразу же сталкиваемся с числами так как нашу дату рождения вес, рост и возраст записываю числами.
Натуральные числа в жизни человека Когда мы идем в школу, класс, получаем оценки и это все записывается числами. Наш урок длится определенное время, у нас определенное количество уроков каждый день, которые определяются в числах.
Натуральные числа в жизни человека На уроках алгебры, геометрии, физики и других предметах мы изучаем цифры во всех их проявлениях.
Натуральные числа в жизни человека Числа нас окружают во всем: когда мы идем домой наш адрес обозначен числами, праздники, цена товара в магазине, ряд и место в кинотеатре, номер телефона, регистрационный номер автомобиля.
Натуральные числа в жизни человека Числа окружают нас всю жизнь, и являются неотъемлемой частью нашей жизни.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-447895
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин призвал повышать уровень общей подготовки в колледжах
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Минздрав включил вакцинацию подростков от ковида в календарь прививок
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Думу внесли законопроект об обязательном образовании для находящихся в СИЗО подростков
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
История появления чисел
По мнению ученых числа появились еще тогда, когда человеку удалось научиться считать окружающие предметы. Это произошло очень и очень давно. Но знаки, обозначающие числа, появились по меркам истории относительно недавно.
Наука считает, что это произошло в 3000-2000 гг. до н. э. Их изобретение приписывают шумерам – народу, проживавшему на территории Месопотамии (в нынешнее время Ирак).
Историки полагают, что глиняные таблички, на которых они выдавливали определенные черточки, привели к изобретению клинописи. Ею обозначали своеобразные разрядные числа: единицы, десятки, сотни, и также они являлись обозначением цифр. Все остальные записи делались при помощи объединения данных знаков.
Использование цифр существенно упрощало подсчеты: вели счет дням недели, количеству голов скота, объемам урожая, считали размеры участков земли. После шумеров в Месопотамии появились вавилоняне. Они получили систему чисел в наследство от шумеров. До наших дней сохранились таблички-клинопись, на которых изображены превращения шумерских единиц для измерений в вавилонские.
Древние египтяне также использовали цифры. Свидетельством тому является находка Ринда – папирус с математическим трактатом, носящим имя изучавшего Египет англичанина и купившего его в 1858 году в стране пирамид. Такой случай представился в Луксоре. Документ содержит записи 84 математических заданий. Все они с решениями. Глядя на папирус, видно использование в Египте такого порядка цифр, где числовое обозначение – это сумма цифровых значений. При обозначении разрядных чисел, кратных десяти: 1, 10, 100, и т.д., египтяне придумали специальный иероглиф. Записывая разные числа, этот символ использовали такое количество раз, сколько в числе единиц данного разряда.
Похожая система счета существовала у римлян. Ей повезло больше других: она оказалась долгожителем среди древних систем счисления. Иногда ее используют и наши современники.
Такие народы, как финикийцы или древние греки, использовали в качестве цифр буквы.
Историки считают, что появление в Индии первых начертаний знакомых нам цифр произошло в 5 веке. Но индийские обозначения чисел появились в Европе лишь в 10-13 веке. Это сделали путешественники с Ближнего Востока. Поэтому их называют «арабские».
Распространение индийских числовых обозначений в арабских странах приписывают работам двух математиков. Это Хорезми, живший ок. 780-ок. 850 гг. в Средней Азии и арабский ученый Кинди (ок.800-ок. 870). Первый, в Багдаде написал трактат о цифрах из Индии. Европейскую известность труд получил после перевода математика из Италии Леонардо Пизанского (Фибоначчи). Эта работа привела к закреплению арабо-индийской числовой системы в Европе.
Такой подход к написанию чисел предполагает зависимость цифрового значения от местоположения при записи. Например, в числе 151 первая единица – это 100, а последняя – один. По-арабски «ноль» – это сифр, что и преобразовалось в «цифру». Арабское обозначение чисел вошло в обиход в Западной Европе в 15 веке.
Арифметика каменного века
Обучаться счету наши предки стали на заре своего развития. Учила их этому окружающая жизнь. Охота была главным способом добычи еды. Чтобы не упустить жертву, ее окружали с разных сторон. Пять человек с одной стороны, четыре с другой. Здесь счет выходил на первое место. Люди, даже не имея понятий о цифрах, обходились показом на пальцах. До сих пор существуют племена, пользующиеся таким видом счета.
Они используют слово «рука» при счете «пять», 10 – это «две руки». Числительное 20 – это «весь человек», при подсчетах учитываются и пальцы ног.
Число 5 – рука, шестерка – это один палец на второй руке. Десятку составляют две руки или полчеловека. Пятнадцать – плюс пальцы одной ноги, двадцать –полностью человек. А вот 23 – это уже плюс 3 пальца на руке соплеменника. Пересчитывая стадо, состоящее из 128 голов, нужно было 7 человек. Вот так счет начинался с того, чем люди обладали с рождения. Может быть, выражение «Знаю, как свои пять пальцев» означало умение считать вообще, знание того, что на одной руке у человека именно пять пальцев.
Археологи, нашедшие поселение древних людей, обнаружили среди волчьих останков кость, с нанесенными отметинами. 55 нанесенных зазубрин указывают на то, что древний охотник вел расчеты при помощи пальцев. Из рисунка на кости можно узнать, что количество зарубок составляет 11 групп по 5 отметин. Начальные 5 групп отделены от других удлиненной отметиной.
Человечество далеко продвинулось вперед с той поры. Но и поныне швейцарские фермеры, отвозя молоко для обработки, зарубками отмечают количество отправляемых емкостей.
Математика, как наука, начиналась с понятий «меньше», «больше», «столько же». Когда племена производили обмен товарами, можно было обойтись без счета. Просто, рядом с товаром, произведенным одним племенем, раскладывали свой собственный. Этого было достаточно, чтобы произвести обмен между людьми.
Для успешного занятия сельским хозяйством, необходимы были знания арифметики. Не рассчитав количество дней, определить время посева, начало полива составляло определенные трудности. Нужно было определять сроки появления приплода у животных, численность скота в загоне, какое количество урожая помещено в амбары.
Примерно за 6 тыс. лет до н. э. скотоводы того времени начали лепить из глины различные предметы для подсчета животных в стаде. Чтобы узнать, все ли стадо вернулось домой, пастух откладывал в сторону один глиняный кружочек за каждую возвратившуюся овцу. Когда число кружочков и количество животных совпадало, считавший шел отдыхать. Его стадо состояло не только из овец. На пастбища выгоняли коров, коз и других животных. Поэтому возникала потребность в изготовлении и других глиняных фигурок. Люди, обрабатывавшие землю, при помощи таких изделий подсчитывали размеры полученного урожая. Число мешков в амбаре, количество выжатого масла в кувшинах. Сколько у него имеется кусков полотна. Все это требовало подсчета. Когда в стаде случался приплод, хозяин добавлял новые кружочки. При забое скота некоторые фигурки приходилось убирать в сторону.
Так, не зная счета, древние совершали арифметические действия.
Получение названий числами
Постоянное перекладывание фигурок из глины – не самое приятное занятие. Также при больших обменах приходилось вначале пересчитать товары, а затем начинался сам процесс сделки. Но до умения пересчитывать предметы, пролетело немало времени. При этом нужно было найти имена для обозначения количества. «Без названия нет знания» – гласит народная мудрость.
Когда именно числа начали называть определенными именами, историки обнаружили, обратившись к языкам этнических групп и народностей. У нивхов, поселившихся на территории Сахалина и Приамурья, обозначение числительных зависит от вещей, которые пересчитывают. Главную роль при подобных подсчетах играет вид предмета. В языке нивхов при подсчетах «двух яиц», «двух камней», «двух глаз»-числа имеют различные названия. На слово «два» у народности приходятся многие десятки слов. Большое количество несхожих наименований одного и того же числа используют и различные африканские народности, и представители народов, живущих в тихоокеанском регионе.
Прошло немало столетий, или даже тысячелетий, чтобы одинаковые числа стали относиться к различным предметам. В это время и возникли универсальные числовые названия.
Историки думают, что первые названия получили числительные 1 и 2. В радиоэфире и телепрограммах нередко употребляются слова «соло», «солист». Так говорят об одном певце или музыканте. Слово пришло из латинского языка. «Солюс» – один. «Солнце» также походит на «солист». Здесь совсем несложная разгадка. Когда римляне искали название единице, то опирались на свои наблюдения, что Солнце в небе постоянно в одиночестве.
Наименование двойки связывают в различных языковых группах с парными объектами. Это глаза, уши, крылья… Но иногда происходило получение числами 1 и 2 других названий. В этих случаях имена чисел привязывали к местоимениям «я» и «ты». В некоторых языках «один» созвучен «мужчине», «два» повторяет слово «женщина». Числа, после двойки, назывались «много». Позже понадобились и наименования другим числам. Ведь собаки, овцы, стрелы у пастуха или охотника чаще всего были в количестве, большем, чем 2. У небольших народностей не так давно совсем отсутствовали числительных, обозначающих количество предметов, больше двух. И здесь нашелся хороший метод для обозначения чисел. Это повторение названий единиц и двоек.
Позже у некоторых народностей появилось имя у числительного, знакомого нам, как число «три». Это слово применялось для употребления вместо «много», следовавшим за первыми двумя числами.
Сердясь на кого-то, мы произносим: «Я что, три раза должен повторять то же самое!».
В русском фольклоре: «Обещанного три года ждут».
Добры молодцы в сказках ходят за «тридевять земель».
«Четыре» встретить в сказаниях можно не так часто. Но и это числительное имело когда-то свое особое значение. Это видно из правил русского языка. Если вслушаться, то говорится: «одна собака», «две собаки». А начиная с числа 5, говорится: «пять собак», «шесть собак» и так сколько угодно. Хоть миллион, но все равно «собак». Это значит, что во времена наших пращуров, при счете, после числительного «четыре», только начиналось неизведанное. Огромное количество чисел, с таинственным названием «много». И эта область простиралась необозримо далеко.
Натуральные числа
Реферат по математике на тему
г. Новосибирск, 2012 год
Для чего нам нужны натуральные числа – 4
Использованная литература – 7
В настоящее время люди не могут обойтись без чисел. Числа окружают нас повсюду, мы сталкиваемся с ними каждую минуту нашей жизни. Из огромного множества чисел самой простой группой являются натуральные числа, с которых мы и начинаем наш счет.
Цель: узнать, на какие виды можно разделить натуральные числа.
Для чего нам нужны натуральные числа.
Натуральные числа применяют для счета предметов. Любое натуральное число можно записать с помощью десяти цифр: 0, 1,2, 3, 4, 5, 6, 7, 8, 9. Цифры являются «кирпичиками» при построении чисел. Для написания числа может быть использована одна или несколько цифр. Такую запись чисел называют десятичной, потому что используется всего 10 различных цифр.
Натуральный ряд бесконечен, у него есть начало, но нет конца, то есть наибольшего натурального числа нет, всегда можно найти натуральное число, которое будет больше.
Самое маленькое натуральное число — единица (1), а каждое следующее число на 1 больше предыдущего.
Значение цифры зависит от ее места в записи числа. Например, цифра 4 означает: 4 единицы, если она стоит на последнем месте в записи числа (в разряде единиц): 4 десятка, если она стоит на предпоследнем месте (в разряде десятков), 4 сотни, если она стоит на третьем месте от конца (в разряде сотен).
Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа «нуль». Это число означает «ни одного». Счет 0 : 3 футбольного матча говорит о том, что первая команда не забила ни одного гола в ворота противника.
Нужно запомнить, что нуль не относят к натуральным числам. Это значит что сам по себе нуль не является натуральным числом, но его часто используют для написания натуральных чисел, чтобы обозначить что в числе нет единиц, или десятков, или сотен.
Виды натуральных чисел.
Если запись натурального числа состоит из одного знака — одной цифры, то его называют однозначным. Например, числа 1, 5, 8 — однозначные.
Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным. Например, числа 14, 33, 28, 95 — двузначные.
Так же по числу знаков в данном числе дают названия и другим числам: числа 386, 555, 951 — трехзначные; числа 1346, 5787, 9999 — четырехзначные и т. д.
Эти группы называют классами. Три первые цифры справа составляют класс единиц, три следующие — класс тысяч, далее идут классы миллионов, миллиардов и т. д.
Миллион — это тысяча тысяч (1000 тыс.). Его записывают: 1 млн или 1
Миллиард — это тысяча миллионов(1000 млн). Его записывают: 1 млрд или 1 000.
Это число имеет 286 единиц в классе единиц, н единиц в классе миллионов и 15 единиц в классе миллиардов.
Чтобы прочитать число, называют слева по очереди число единиц каждого класса и добавляют название класса:
Не произносят название класса единиц, а также класса, все три цифры которого — нули.
15 миллиардов 389 миллионов 286. (тысяч нуль, поэтому не произносим).
Теперь можно с уверенностью сказать, что натуральные числа можно разделить на несколько видов. А при чтении натуральных чисел, нужно быть очень внимательным.
Натуральные числа для чего людям понадобились эти числа
Можно ли представить мир без чисел? Вспомните, что мы с вами делаем изо дня в день: без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие достижения! Они были бы попросту невозможны, если бы не наука о числах.
Число одно из основных понятий математики, позволяющее выразить результаты счета или измерения.
КАК ПОЯВИЛИСЬ ЦИФРЫ И ЧИСЛА.
1. Арифметика каменного века.
Сначала люди научились узнавать число предметов или животных, делая особые зарубки на счетных палочках, вести счет.
Мысль о счете пришла людям в голову раньше, чем появились цифры. Люди могли сообщить друг другу, что в одном стаде животных больше чем в другом, а вот, сколько именно – сосчитать не умели.
Несколько десятков лет назад ученые-археологи обнаружили стойбище древних людей. В нем они нашли волчью кость, на которой 30 тысяч лет тому назад какой-то древний охотник нанес 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам. Узор на кости состоял из 11 групп, по 5 зарубок в каждой. При этом первые 5 групп он отделил от остальных длинной чертой. Позднее в Сибири и других были найдены сделанные в ту далекую эпоху каменного века (каменные орудия) и украшения, на которых тоже были черточки и точки, сгруппированные по 3, по 5 или по 7. Много тысячелетий прошло с того времени. Но и сейчас швейцарские крестьяне, отправляя молоко на сыроварни, отмечают число фляг такими же зарубками. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером или надписью, которую привязывают к кулям с товаром, ящикам и тюкам и т.д. А еще двести –триста лет назад это слово означало совсем иное. Так называли куски дерева, на которых зарубками отмечали сумму долга и подати. Бирку с зарубками раскладывали пополам, после чего одна половинка оставалась у должника, а другая у сборщика податей. При счёте
половинки складывали вместе, и это позволяло определить сумму долга или подати без спора и сложных вычислениях.
Они могли представить себе такие числа как один, два, три. Все другие числа они означали понятием «Много». Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
В древние времена, когда человек хотел показать, сколькими животными он владел, он клал в большой мешок столько камешков, сколько у него было животных. Чем больше животных, тем больше камешков. Отсюда и произошло слово «калькулятор», «калькулюс» по латински означает «камень».
Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги. Поэтому, если в те времена кто-то хвалился, что у него «две руки и одна нога кур», это означало, что у него пятнадцать кур, а если это называлось «весь человек», то есть две руки и две ноги.
Перуанские инки вели счет животных и урожая, завязывая узелки на ремешках или шнурках разной длины и цвета (Рис. 1). Эти узелки назывались кипу. У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают 4 узелочка шнурочке! Поэтому того, кто завязывал узелки, называли вспоминателем.
Первыми придумали запись чисел древние шумеры. Они пользовались всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а угол из двух лежачих чёрточек – десять. Эти чёрточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали. Вот так выглядели эти дощечки (Рис. 2).
После счета по зарубкам люди изобрели особые символы, названные цифрами. Они стали применяться для обозначения различных количеств каких-либо предметов. Разные цивилизации создавали свои собственные цифры.
Так, например, в древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел 1, 10, 100, 1000, …: (Рис. 3).
Для того чтобы изобразить, например, целое число 23145, достаточно записать в ряд два иероглифа, изображающие десять тысяч, затем три иероглифа для тысячи, один – для ста, четыре – для десяти и пять иероглифов для единицы: (Рис.4).
Этого одного примера достаточно, чтобы научиться записывать числа так, как их изображали древние египтяне. Это система очень проста и примитивна.
В начале нашей эры индейцы племени майя, которые жили на полуострове Юкатан в Центральной Америке, пользовались другой системой счисления – двадцатеричной. Они обозначали 1 точкой, а 5 – горизонтальной чертой, например, запись ‗‗‗‗‗‗ означала 14. системе счисления майя был и знак для нуля. По своей форме он напоминал полузакрытый глаз.
В Древней Греции сначала числа 5, 10, 100, 1000, 10000 обозначали буквами Г, Н, Х, М, а число 1 – черточкой /. Из этих знаков составляли обозначения r r r Г (35) и т.д. Позднее числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000, 20000 стали обозначать буквами греческого алфавита, к которому пришлось добавить еще три устаревшие буквы. Чтобы отличить цифры от букв, над буквами ставили черточку.
Древние индийцы изобрели для каждой цифры свой знак. Вот как они выглядели (Рис.5)
Они похожи на многие наши цифры. Слово «цифра» тоже досталось нам от арабов по наследству. Арабы нуль, или «пусто», называли «сифра». С тех пор и появилось слово «цифра». Правда, сейчас цифрами называются все десять значков для записи чисел, которыми мы пользуемся: 0, 1, 2,3,4,5,6,7,8,9.
Постепенное превращение первоначальных цифр в наши современные цифры.
Из всех странных нумераций римская является единственной, сохранившейся до сих пор и довольно широко применяемой. Римские цифры употребляются и сейчас для обозначения столетий, нумерации глав в книгах и др.
1 5 10 50 100 500 1000
С их помощью можно записать любое число не больше 4000. Некоторые числа записываются при помощи повторения римских цифр:
III = 3 · 1 = 3, XX = 2 · 10 = 20.
Кроме того, используется принцип сложения и вычитания. Если меньшая по значению буква стоит после большей, то их значения складывают:
VI = 5 + 1 = 6, MC = 1000 + 100 = 1100
Если меньшая цифра стоит перед большей, то из большего вычитают меньшее:
IV = 5 – 1 = 4, СМ = 1000 – 100 = 900.
(ХХХ VI = 3 · 10 + (5 + 1) = 36,
CXLV = 100 + (50 – 10) + 5 = 145.)
Наши предки пользовались алфавитной нумерацией, то есть числа изображались буквами, над которыми ставился значок
, называемый «титло». Чтобы отделить такие буквы – числа от текста, спереди и сзади ставились точки.
Этот способ обозначения цифр называется цифирью. Он был заимствован славянами от средневековых греков – византийцев. Поэтому цифры обозначались только теми буквами, для которых есть соответствия в греческом алфавите (Рис. 7).
Для обозначения больших чисел славяне придумали свой оригинальный способ:
Десять тысяч – тьма,
десять тем – легион,
десять легионов – леорд,
десять леордов – ворон,
десять воронов – колода.
Такой способ обозначения чисел по сравнению с принятой в Европе десятичной системой был очень неудобен. Поэтому Пётр I ввёл в России привычные для нас десять цифр, отменив буквенную цифирь.
Вот до какого огромного числа простирается натуральный ряд. Но и это число не последнее. За ним еще числа, числа, числа, числа… до бесконечности. Если натуральный ряд чисел кажется вам скучным и однообразным, всмотритесь в него повнимательнее, и вы найдете много удивительного и неожиданного.
Например, обыкновенное число 37. А теперь умножьте его на три, потом на шесть и так далее… На этом чудеса числа 37 не кончаются. Возьмем любое трехзначное число, которое делится на 37. Пусть это будет 185. И сделаем в нем круговую перестановку – последнюю цифру поставим на первое место, не изменив порядка остальных. Получим 518. Сделаем еще одну перестановку. Получим 851. Оба эти числа также делятся на 37. Вот вам и диковинка!
Первые математики считали по пальцам одной руки. До пяти. А если предметов было больше, то говорили «пять и один», «пять и два»… Так возникла пятеричная система счисления. Потом пальцев руки стало недостаточно и появилось десятеричная система счисления – на пальцах обеих рук. Дальше – больше. Человеку пришлось «разуться» и считать по пальцам рук и ног. Возникла двадцатеричная система счисления.
Но и этого, как вы понимаете, оказалось мало. Тогда придумали шестидесятеричную систему. Стали считать тройками, по числу суставов на каждом пальце левой руки без большого пальца, то есть до двенадцати. Каждый палец левой руки означал 12. Если один палец это 12, то пять пальцев – это 60.
И, наконец, счет так усложнился, что людям пришлось изобрести цифры для обозначения числа, которых становилось все больше и больше. Разные народы изобретали свои цифры для записи чисел.
Шестидесятеричную систему изобрели древние вавилоняне. В наследство от них нам осталось деление суток на 24 или 12 двойных часов, деление часа на 60 минут, а минут на секунды и деление круга на 360 градусов.
А самой удобной оказалась десятеричная система, та самая, которой мы пользуемся и сегодня. Цифры, которыми мы записываем числа, называются арабскими. Их всего 10. Изобретены эти цифры были в Индии, но получили название арабских, потому что в Европу пришли из арабских стран. Многие годы форма цифр совершенствовалась и теперь принята во всем мире. Так постепенно зарождалась математика. Человек незаметно очутился в мире чисел. И оказалось, что в этом мире его ждет много удивительного и даже таинственного…
Когда-то числа служили только для решения практических задач. А потом их стали изучать, узнавать их свойства. С помощью чисел выражали и такие понятия, как справедливость, дружба. Ученые установили, как по записи числа узнавать, на какие другие числа оно делится. Они научились находить простые числа и стали изучать их свойства. Иногда открытия в науке о числах делали совсем юные математики. Математику применяют и для шифрования и для расшифровки донесений разведчиков, сообщений дипломатов, военных приказов. Некоторые методы шифровки и расшифровки сообщений основаны на свойствах чисел, в частности на особой арифметике, которую. Называют арифметикой остатков.
1. Депман И.Я., Виленкин Н.Я. За страницами учебника матема ики. – М.: Просвещение, 1989.
2. Крейг А. и Росни К. Наука. Энциклопедия. – М.: «Росмэн», 1994.
3. Математика: Учебник-собеседник для 5-6 классов средней школы / Шаврин Л.Н., Гейн А.Г., Коряков И.О., М.В. Волков М.В. – М.: Просвещение, 1989.
4. Ризванова Х.Я. Книга для внеклассного чтения по математике. – Уфа: Китап, 1998.
5. Шпорер З. Ох, эта математика! – М.: педагогика, 1985.
6. Энциклопедический словарь юного математика / Сост. Савин А.П. – М.: Педагогика, 1989.