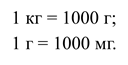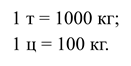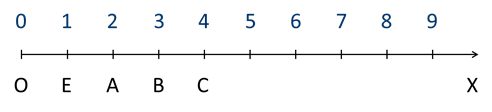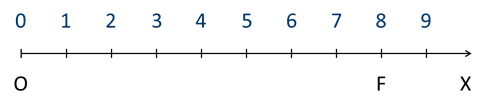Натуральные координаты 5 класс что это
Шкалы. Координатный луч
Содержание
Для измерения длины отрезка используется линейка. Измерение возможно за счет того, что на линейку нанесена шкала — это штрихи через одинаковые промежутки.
На школьный линейках, как правило, расстояние между штрихами равно 1 мм, оно называется делением.
Дополнительно на линейках обозначены и сантиметровые интервалы — под удлиненными штрихами стоят цифры. Один сантиметровый отрезок содержит в себе 10 делений по 1 мм.
Шкалу также можно увидеть в термометре. Там одно деление соответствует одному градусу, цифрами обозначены величины, равные 10, 20, 30 градусам и т.д.
Еще шкала бывает на весах. Обычно одно деление весов равно 100 гр. Цифрами обозначены величины в 1, 2, 3 кг и т. д.
Но если нужно взвешивать большие предметы, то применяются весы, деление шкалы в которых больше чем 100 гр. В этом случае используются такие единицы измерения массы, как тонна и центнер.
1 тонна обозначается как 1 т, 1 т = 1000 кг.
1 центнер обозначается как 1 ц, 1 ц = 100 кг.
Шкала также есть на таком приборе, как динамометр
Координатный луч
В математике шкалу можно встретить на координатном луче. Разберем подробнее, что это за луч и как его построить.
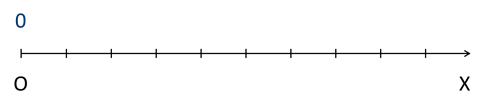
Начертим луч ОХ, как показано на рисунке 1.
Рисунок 1
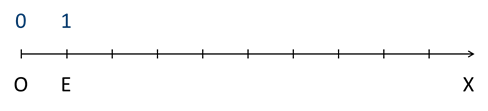
Точка О является его началом. Она соответствует числу 0. От точки О вправо отложим отрезок, равный 1 см, а полученную точку обозначим Е (рисунок 2).
Рисунок 2
Точка Е будет соответствовать числу 1. Отрезок ОЕ называется единичным.
Таким образом, луч ОХ стал координатным лучом, где О — это начало координат, а ОЕ — единичный отрезок. (Единичный отрезок в нашем примере равен 1 см, но он может быть любой длины, именно это длина будет приниматься на координатном луче за единицу измерения.)
Числа, соответствующие точкам на координатном луче, называются координатами этих точек. Говорят так: точка О имеет координату 0, точка Е имеет координату 1. Записывается это следующим образом: О(0), Е(1).
Рисунок 3
Отметим на координатной луче точки А(2), В(3), С(4) — рисунок 3. Так мы получили на координатном луче шкалу, которую можно продолжать бесконечно.
Шкалы и координаты
Урок 5. Математика 5 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Шкалы и координаты»
На этом уроке мы поговорим о величинах. Посмотрим, как измеряются различные величины и для чего они используются. Разберёмся в понятиях «шкала», «координатный луч» и «координата».
К уроку вы должны были подготовиться и принести линейки. Положите, пожалуйста, линейку перед собой.
Обратите внимание на то, что у всех они разные: разного цвета, разного материала и разной длины. Но все линейки имеют общие черты – на них нанесены штрихи.
Все штрихи находятся на одинаковом расстоянии друг от друга. Около некоторых штрихов написаны числа. Все штрихи на линейке разбивают её на равные части. Эти части называют делениями. Длину деления называют ценой. Цена деления на вашей линейке равна 1 мм. Все деления линейки вместе с написанными числами образуют шкалу. Линейки используют для измерения длины.
Давайте измерим длину отрезка АВ.
Приложим к нему линейку.
Видим, что длина отрезка АВ равна 6 см.
Шкалы имеют и другие измерительные приборы, например комнатный термометр.
Используют его для измерения температуры. Его шкала состоит из 55 делений. Каждое деление соответствует одному градусу Цельсия. Посмотрите: какую температуру показывает термометр на рисунке? Правильно! 15 °С.
Шкалы могут иметь различные формы. Например, спидометр:
На его шкале на промежутке от 0 км/ч до 20 км/ч содержится 4 деления. Поэтому одному делению шкалы соответствует 20 км/ч : 4 = 5 км/ч. Значит, каждое деление спидометра соответствует 5 км/ч. С помощью спидометра контролируют скорость автомобиля.
На весах тоже бывают шкалы:
На рисунке видно, что масса яблок равна 2 кг. При взвешивании меньших предметов применяют единицы массы: грамм (г) и миллиграмм (мл).
При взвешивании больших предметов применяют единицы массы: тонну (т) и центнер (ц).
А вспомним механические часы или часы с циферблатом:
Со шкалами мы разобрались, а теперь давайте перейдём к чертежам. Начертим луч ОХ, так чтобы он шёл слева направо. Его начало, точку О, пометим числом 0.
Отметим на луче ОХ некоторую точку Е и пометим её числом 1. Получили отрезок ОЕ, его длину примем равной единице.
Такой отрезок называют единичным отрезком.
Отложим на луче ОХ вправо от точки Е такой же единичный отрезок. Получим новую точку, обозначим её А, а над ней запишем число 2. Повторим это ещё раз, получим точку В, которую пометим числом 3. Этот процесс можно повторить бесконечное количество раз. В результате получится бесконечная шкала.
Её называют координатным лучом, а точку О – началом отсчёта.
И так как конца у координатного луча нет, то завершим его стрелочкой, которая нам будет показывать, что числа продолжаются и дальше.
Натуральное число изображается определённой точкой координатного луча. Например, число 3 изображается точкой В. Говорят, что число 3 является координатой точки В или точка В имеет координату 3.
Это записывают так: В (3).
Координата точки показывает расстояние от этой точки до начала координат, измеренное единичным отрезком.
На рисунке точка F имеет координату 8. Это говорит о том, что расстояние от точки F до точки О равно 8, или отрезок ОF имеет длину 8 (ОF = 8).
Итак, сегодня на уроке мы рассмотрели различные величины и их единицы измерения. Узнали такое понятие, как шкала. Научились строить координатный луч и находить точки по их координатам.
Шкалы, координаты
Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.
Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.
Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).
Рисунок 1. Измерительная линейка.
Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.
Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).
Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.
Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.
Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.
Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.
Рисунок 2 Цена деления шкалы
Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?
Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:
Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.
Координатный луч, единичный отрезок, координаты точки
Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.
Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.
Рис. 3. Луч с началом в точке O
Рис. 4. Луч с равными отрезками
Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).
Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.
Рис. 5. Луч с отрезками и цифрами
Покажу еще раз на примере точки S :
так как RS=OP (по условиям построения данных отрезков),
подставив известные нам значения длины отрезков OR и OP, получим:
Значит, точке S на нашем лучу соответствует число 3.
Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.
Рис. 6. Координатный луч
Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.
Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.
Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.
Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.
Координатный луч — это не что иное, как бесконечная шкала.
Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.
Рис. 7. Разные варианты единичного отрезка
Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).
Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.
Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.
Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.
Рис. 8. Координаты точек
Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).
В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.
Рис. 9. Большие числа на координатном луче.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.2 / 5. Количество оценок: 9
Натуральные числа и координатный луч. 5-й класс
Разделы: Математика
Класс: 5
Цели урока:
Оборудование:
Тип урока: урок по комплексному применению знаний и способов деятельности.
Логика урока:
Мотивация —> актуализация знаний и способов деятельности —> самостоятельное применение знаний в различных ситуациях —> самоконтроль и контроль —> коррекция —> рефлексия.
Система упражнений для повторения делится:
Устные упражнения предназначены для фронтальной работы с учащимися (при выполнении требуется подробное обоснование ответа или решения).
При выполнении письменных упражнений определяется способ решения, выполняются необходимые преобразования.
Ход урока
I. Организационный момент.
Вступительное слово учителя. Определение целей урока.
Рефлексия: ребята, у вас на партах лежат по три фигурки: круг, квадрат, треугольник. Поднимите ту фигурку, которая соответствует вашему настроению.
II. Актуализация знаний учащихся по теме «Натуральные числа и координатный луч».
III. Применение знаний, умений и способов действий по теме.
Учитель: Ребята, откройте рабочие тетради и напишите число, классная работа. У вас на парте лежат листы с заданиями.
К доске вызываю по 1 ученику, он решает, класс проверяет, ошибки анализируются. Для того, чтобы оценить ответ работающего у доски, выдаю ему карточку с дополнительным заданием. Работа выполняется на боковой доске, проверяю сама.
Провести физкультминутку: разминку для глаз, для кистей рук, для шеи.
IV. Самостоятельная работа (тестирование)
Учитель: А теперь, ребята, пришло время для подготовки к нашему будущему экзамену. На парте у вас лежат тестовые задания. На эту работу я отвожу вам 15 минут. По истечении этого времени работы сдаются. Приложение 3.
V. Подведение итогов урока.
Учитель: Итак ребята, сегодня на нашем уроке мы повторили с вами что такое натуральные числа, многозначные числа, какие математические действия с натуральными числами можно выполнять; что.такое координатный луч и как отмечаются на нем координаты точек. Вы все молодцы. Все хорошо работали, особенно (ФИ ученика). Отметки получили следующие ребята.
На ваших листах, с которыми мы работали на уроке, во второй колонке записано: домашняя работа. Откройте дневники и запишите д.з. на следующий урок: карточка. Выполнять д.з. вы будете на этих листах. На них подпишите свою фамилию. Задания на дом аналогичные тем, которые мы решали с вами на уроке. Если у кого-то возникнут трудности, на следующем уроке мы их разберем
Рефлексия: Спасибо вам за урок. Мое настроение к концу урока не испортилось, оно такое же яркое и светлое, как кружок. А какое настроение у вас?
Урок 7 Бесплатно Координатный луч
Ответим на вопрос, почему луч подходит больше всего для обозначения натуральных чисел, а также научимся определять с помощью него длины отрезков.
Определение
Луч- это часть прямой ограниченная с одной стороны точкой, называемой началом луча.
Начертим луч с началом в точке О так, чтобы он шел слева направо, и отметим на нем точку А не очень далеко от начала.
Отрезок ОА назовем единичным отрезком.
Далее отложим от точки А следующий отрезок АВ, равный отрезку ОА.
Затем отложим от точки В отрезок ВС, также равный единичному отрезку.
Продолжим процесс, уже не называя точки.
Так мы получили шкалу, которую называют координатным лучом.
В самом деле, для шкалы нам необходимы были такие объекты, как штрих, деление, цена деления, посмотрим, чем они представлены в данном случае.
В роли штрихов выступают точки.
Изображая координатный луч, можно точки обозначать как небольшие штрихи, это ничуть не делает рисунок менее точным.
Делением в данном случае является отрезок между любыми соседними точками.
Этот отрезок всегда равен единичному по построению, ведь мы всегда откладывали отрезок, равный единичному.
Ценой деления в данном случае является единица.
Может быть немного непривычно, что единица идет без наименования, ведь на других шкалах обычно цена деления 1 кг, 1 см, 1 км/ч.
Но здесь идет измерение натуральных чисел, поэтому просто единица.
Так что координатный луч вполне можно считать шкалой.
Если же говорить про более конкретное определение, то вот оно.
Нередко к этому определению добавляют помимо единичного отрезка еще два объекта: точку начала отсчета и направление увеличения чисел.
А на координатном луче точка начала отсчета и точка начала луча всегда совпадают.
Направление задавать тоже нет необходимости, ведь у луча только одно вполне определенное направление: от начала.
Единичный отрезок же необходим, ведь без него не будет одинакового расстояния между соседними точками и смысла в луче не будет.
Отметим важный момент: в одном координатном луче всегда один единичный отрезок.
Пройти тест и получить оценку можно после входа или регистрации
Координаты
Мы уже поговорили про координатный луч, но важно понять, почему он “координатный” и как определены координаты в данном случае.
Обычно можно услышать слово “координаты” в географическом контексте.
Когда мы узнаем координаты, а это два числа, то можем однозначно сказать, про какую точку на карте идет речь.
Другими словами, в географическом смысле, координаты являются числами, определяющими положение точки на карте.
В случае с координатным лучом все даже проще.
Координата точки на координатном луче соответствует количеству единичных отрезков между этой точкой и точкой начала отсчета.
Посмотрим еще раз на рисунок из прошлой главы:
Точка А находится на расстоянии одного единичного отрезка от точки начала отсчета.
Точке А соответствует число 1
Точка В находится на расстоянии двух единичных отрезков от точки начала отсчета.
И точке В соответствует число 2
Аналогично каждой следующей точке соответствует число на единицу больше.
Число, соответствующее точке на координатном луче, называют координатой этой точки.
Заметим теперь, как соответствуют друг другу натуральный ряд и координатный луч.
За исключением точки начала отсчета, каждой точке соответствует натуральное число.
Если смотреть от начала отсчета, то координата следующей точки после данной равна следующему натуральному числу после координаты данной точки.
И также мы знаем, что координата точки P равняется 276
Тогда мы сможем сказать координату точки Q, это будет следующее натуральное число после числа 276, то есть ответ: 277
Аналогичная логика работает и в другую сторону.
Координата точки, идущей перед данной, является предыдущим натуральным числом по отношению к координате данной точки.
Допустим, точки E и R соседние.
Также известно, что R находится дальше от точки начала отсчета, чем Е; а также известна координата точки R, она равна 315
Чтобы найти координату точки Е достаточно взять предыдущее натуральное число от числа 315, это будет число 314
Эти примеры показывают, как натуральный ряд ложится на координатный луч.
Отметим, что именно луч идеально соответствует натуральным числам, ведь и луч, и натуральный ряд ограничены с одной стороны (с начала), но продолжаются бесконечно.
Если же нам надо найти координату точки безотносительно соседних точек, то достаточно отсчитать количество единичных отрезков между данной точкой и точкой начала отсчета.
Найдем координату точки Н.
Между ей и точкой О (началом отсчета) 4 единичных отрезка, значит, координата точки Н равна 4
Пройти тест и получить оценку можно после входа или регистрации