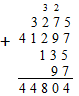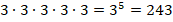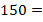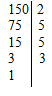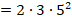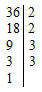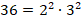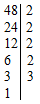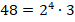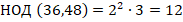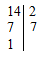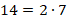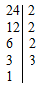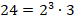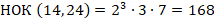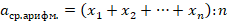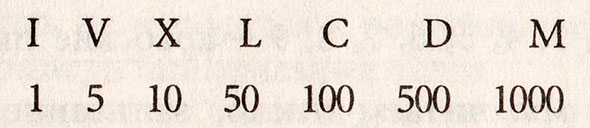Натуральный ряд в математике что это такое
Натуральные числа
Натуральные числа: определение, операции, свойства
Определение
Натуральными числами называются числа, предназначенные для счета предметов. Для записи натуральных чисел используются 10 арабских цифр (0–9), положенных в основание общепринятой для математических расчетов десятичной системы счисления.
Последовательность натуральных чисел
Иногда в ряд натуральных чисел вводят и 0. Это допустимо, и тогда говорят о расширенном натуральном ряде.
Классы натуральных чисел
Каждая цифра натурального числа выражает определенный разряд. Самая последняя – это всегда количество единиц в числе, предыдущая перед ней – количество десятков, третья от конца – количество сотен, четвертая – количество тысяч и так далее.
Для больших и очень больших чисел можно увидеть устойчивую тенденцию (если исследовать число справа налево, то есть от последней цифры к первой):
То есть всякий раз мы имеем дело с тремя цифрами, означающими единицы, десятки и сотни более крупного наименования. Такие группы формируют классы. И если с первыми тремя классами в повседневной жизни приходится иметь дело более или менее часто, то другие следует перечислить, потому что далеко не все помнят наизусть их названия.
Сложение натуральных чисел
Сложение натур.чисел представляет собой арифметическое действие, позволяющее получить число, в котором содержится столько же единиц, сколько имеется в складываемых числах вместе.
Знаком сложения является знак «+». Складываемые числа называются слагаемыми, получаемый результат – суммой.
Небольшие числа складывают (суммируют) устно, письменно такие действия записывают в строку.
Многозначные числа, которые прибавлять в уме затруднительно, принято складывать в
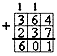
Если в столбик складывается не 2, а больше чисел, то при суммировании цифр разряда избыточным может оказаться не 1 десяток, а несколько. В этом случае на следующий разряд переносится количество таких десятков.
Вычитание натуральных чисел
Вычитание – это арифметическое действие, обратное сложению, которое сводится к тому, что по имеющейся сумме и одному из слагаемых нужно найти другое – неизвестное слагаемое. Число, из которого вычитают, называется уменьшаемым; число, которое вычитают, – вычитаемым. Результат вычитания называют разностью. Знак, которым обозначают действие вычитания, является «–».
При переходе к сложению вычитаемое и разность превращаются в слагаемые, а уменьшаемое – в сумму. Сложением обычно проверяют правильность выполненного вычитания, и наоборот.
Здесь 74 – уменьшаемое, 18 – вычитаемое, 56 – разность.
Обязательным условием при вычитании натуральных чисел является следующее: уменьшаемое обязательно должно быть больше вычитаемого. Только в этом случае полученная разность тоже будет натуральным числом. Если действие вычитания осуществляется для расширенного натурального ряда, то допускается, чтобы уменьшаемое было равно вычитаемому. И результатом вычитания в этом случае будет 0.
Примечание: если нулю равно вычитаемое, то операция вычитания не изменяет величины уменьшаемого.
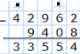
Вычитание многозначных чисел обычно производят в столбик. Записывают при этом числа так же, как и для сложения. Вычитание выполняется для соответствующих разрядов. Если же оказывается, что уменьшаемое меньше вычитаемого, то берут единицу из предыдущего (находящегося слева) разряда, которая после переноса, естественно, превращается в 10. Эту десятку суммируют с цифрой уменьшаемого данного разряда и после этого производят вычитание. Далее при вычитании следующего разряда обязательно учитывают, что уменьшаемое стало на 1 меньше.
Произведение натуральных чисел
Произведение (или умножение) натуральных чисел – это арифметическое действие, представляющее собой нахождение суммы произвольного количества одинаковых слагаемых. Для записи действия умножения используют знак «·» (иногда «×» или «*»). Например: 3·5=15.
Действие умножение незаменимо при необходимости складывать большое количество слагаемых. Например, если нужно число 4 прибавить 7 раз, то перемножить 4 на 7 проще, нежели выполнять такое сложение: 4+4+4+4+4+4+4.
Числа, которые перемножают, называются множителями, результат умножения – произведением. Соответственно, термин «произведение» может в зависимости от контекста выражать собой как процесс умножения, так и его результат.
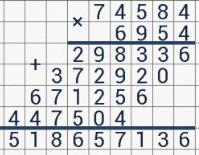
Многозначные числа перемножают в столбик. Для этого числа записывают так же, как и для сложения и вычитания. Рекомендуется первым (выше) записывать то из 2-х чисел, которое длиннее. В этом случае процесс умножения будет более простым, а следовательно, более рациональным.
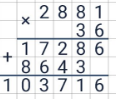
При умножении в столбик выполняют последовательное умножение цифры каждого из разрядов второго числа на цифры 1-го числа, начиная с его конца. Найдя первое такое произведение, записывают цифру единиц, а цифру десятков держат в уме. При умножения цифры 2-го числа на следующую цифру 1-го числа к произведению прибавляют ту цифру, которую держат в уме. И снова записывают цифру единиц полученного результата, а цифру десятков запоминают. При умножении на последнюю цифру 1-го числа полученное таким способом число записывают полностью.
Результаты умножения цифры 2-го разряда второго числа записывают вторым рядом, сместив его на 1 клетку вправо. И так далее. В итоге будет получена «лесенка». Все получившиеся ряды цифр следует сложить (по правилу сложения в столбик). Пустые клетки при этом нужно считать заполненными нулями. Полученная сумма и есть конечное произведение.
Примечание
Деление натуральных чисел
Делением называют арифметическое действие, с помощью которого по известному произведению и одному из множителей может быть найдет другой – неизвестный – множитель. Деление является действием, обратным умножению, и используется для проверки правильности выполненного умножения (и наоборот).
Число, которое делят, называют делимым; число, на которое делят, – делителем; результат деления называется частным. Знаком деления является «:» (иногда, реже – «÷»).
Здесь 48 – делимое, 6 – делитель, 8 – частное.
Не все натуральные числа можно поделить между собой. В этом случае выполняют деление с остатком. Заключается оно в том, что для делителя подбирается такой множитель, чтобы его произведение на делитель было бы числом, максимально близким по значению к делимому, но меньшим него. Делитель умножают на этот множитель и вычитают его из делимого. Разность и будет остатком от деления. Произведение делителя на множитель называют неполным частным. Внимание: остаток обязательно должен быть меньше подобранного множителя! Если остаток больше, то это означает, что множитель подобран неверно, и его следует увеличить.
где a – перемножаемое само на себя число, x – количество таких множителей.
Простые и составные натуральные числа
Всякое натуральное число, кроме 1, можно разделить как минимум на 2 числа – на единицу и на само себя. Исходя из этого критерия, натуральные числа разделяют на простые и составные.
Простыми считаются числа, которые делятся только на 1 и на само себя. Числа, которые делятся более чем на эти 2 числа, называют составными. Единица, делящаяся исключительно на саму себя, не относится ни к простым, ни к составным.
Простыми являются числа: 2,3,5,7,11,13,17,19 и т.д. Примеры составных чисел: 4 (делится на 1,2,4), 6 (делится на 1,2,3,6), 20 (делится на 1,2,4,5,10,20).
Всякое составное число можно разложить на простые множители. Под простыми множителями при этом понимаются его делители, являющиеся простыми числами.
Пример разложения на простые множители:
Делители натуральных чисел
Под делителем понимают число, на которое можно без остатка разделить данное число.
В соответствии с этим определением, простые натур.числа имеют 2 делителя, составные – больше 2 делителей.
Многие числа имеют общие делители. Общим делителем называется число, на которое данные числа делятся без остатка.
Особое значение имеет наибольший общий делитель (НОД). Это число, в частности, полезно уметь находить для сокращения дробей. Для его нахождения требуется разложить данные числа на простые множители и представить его как произведение их общих простых множителей, взятых в наименьших своих степенях.
Требуется найти НОД чисел 36 и 48.
Делимость натуральных чисел
Далеко не всегда представляется возможным «на глазок» определить, делится ли одно число на другое без остатка. В таких случаях полезным оказывается соответствующий признак делимости, то есть правило, по которому за считанные секунды можно определить, можно ли разделить числа без остатка. Для обозначения делимости используется знак «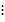
Наименьшее общее кратное
Эта величина (обозначается НОК) представляет собой наименьшее число, которое делится на каждое из заданных. НОК может быть найден для произвольного набора натуральных чисел.
НОК, как и НОД, имеет значительный прикладной смысл. Так, именно НОК нужно находить, приводя обыкновенные дроби к общему знаменателю.
НОК определяется путем разложения заданных чисел на простые множители. Для его формирования берется произведение, состоящее из каждого из встречающихся (хотя бы для 1 числа) простых множителей, представленных в максимальной степени.
Требуется найти НОК чисел 14 и 24.
Среднее арифметическое
Средним арифметических произвольного (но конечного) количества натуральных чисел является сумма всех этих чисел, разделенная на количество слагаемых:
Среднее арифметическое представляет собой некоторое усредненное значение для числового множества.
Даны числа 2,84,53,176,17,28. Требуется найти их среднее арифметическое.
Понятие о натуральном числе
Натуральные числа и десятичная запись числа
Чтобы сосчитать некоторое количество предметов, используются числа, которые называют натуральными.
С помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можно записать любое натуральное число. (подобным образом мы используем буквы алфавита, чтобы записать слова)
Такую запись числа называют десятичной ‒ десять единиц каждого разряда составляют одну единицу следующего старшего разряда.
Натуральный ряд
Если натуральные числа записать в порядке возрастания, то получится ряд натуральных чисел ‒ натуральный ряд.
Каждое число в этом ряду меньше последующего на единицу. Наименьшее число среди натуральных чисел — это 1, а наибольшего числа нет.
Многозначные числа
Натуральное число называют однозначным, если его запись состоит из одного знака — одной цифры.
Например, числа 3, 7, 9 — однозначные.
Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным.
Например, числа 25, 44, 65, 80 — двузначные.
Числа 100, 543, 888 — трёхзначные:
Числа 2000, 6791, 1060 — четырёхзначные и т. д.
Двузначные, трехзначные, четырёхзначные, пятизначные и т. д. — это многозначные числа.
Классы и разряды
Прочитать записи однозначных, двузначных и трехзначных чисел (например: 7, 54, 976) затруднений не вызывает.
Чтобы прочесть многозначное натуральное число, его необходимо разбить справа налево на группы по три цифры в каждой. Крайняя левая группа может состоять из одной или двух цифр.
Эти группы называют классами.
Три первые цифры справа ‒ это класс единиц, три следующие — класс тысяч, затем класс миллионов, класс миллиардов и т. д.
Место, занимаемое цифрой в записи числа, называют разрядом.
Если считать справа налево, то первое место в записи числа называют разрядом единиц, второе — разрядом десятков, третье — разрядом сотен и т. д.
Например, в числе 5034 имеем 4 единицы разряда единиц, 3 единицы разряда десятков, 0 единиц разряда сотен и 5 единиц разряда тысяч.
Можно также сказать, что в классе единиц 34 единицы.
Названия некоторых больших чисел
1 тысяча (1 тыс.) – 1 000 (тысяча)
1 миллион (1 млн) – 1 000 000 (тысяча тысяч)
1 миллиард (1 млрд) – 1 000 000 000 (тысяча миллионов)
1 триллион (1 трлн) – 1 000 000 000 000 (тысяча миллиардов)
Рассмотрим число 6 000 126 754.
Его читают: 6 миллиардов 126 тысяч семьсот пятьдесят четыре.
В классе миллионов во всех разрядах стоят нули. Поэтому при чтении числа 6 000 126 754 не произносят название этого класса.
Примеры прочтения чисел:
а) Число 200 700 читается так: двести тысяч семьсот;
б) Число 6 000 008 читается так: шесть миллионов восемь;
в) Число 14 000 002 000 читается так: четырнадцать миллиардов две тысячи.
Значение цифры в записи числа
Значение цифры зависит от её позиции (места) в записи числа.
Например, в записи числа 56 978 цифра 8 означает 8 единиц, так как она стоит на последнем месте в записи числа (в разряде единиц);
В записи числа 42 389 цифра 8 означает 8 десятков, так как она стоит на предпоследнем месте в записи числа (в разряде десятков);
В записи числа 5 300 847 цифра 8 означает 8 сотен, так как она стоит на третьем месте от конца в записи числа (в разряде сотен).
Число 0 и цифра 0
Число 0 натуральным не является.
Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа «нуль» (что означает ‒ «ни одного»).
(Например, счёт 1 : 0 хоккейного матча говорит о том, что вторая команда не забила ни одной шайбы в ворота противника.)
Поделись с друзьями в социальных сетях:
Что такое Натуральное число
Определение натурального числа
Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.
Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.
Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.
Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.
Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).
Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.
Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.
Множество натуральных чисел
Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:
Натуральные числа:
Натуральные числа с нулём:
Ряд натуральных чисел
Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:
Наибольшего натурального числа не существует — натуральный ряд бесконечен.
Ненатуральные числа
Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).
Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;
Свойства натуральных чисел
Натуральные числа обладают следующими свойствами:
Что такое натуральные числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое НАТУРАЛЬНЫЕ ЧИСЛА.
С ними человек встречается с самого рождения. Например, когда считает пальцы на руке – 1, 2, 3, 4, 5. Или отмечает праздники – 8 марта, 23 февраля, 9 мая, 31 декабря.
Натуральные числа — это.
Натуральные числа – это те числа, которые возникают при подсчете чего-либо. Например, одно яблоко, два яблока, пять яблок десять яблок и так далее.
Лучше даже представить, что вы подсчитываете людей, ибо их нельзя поделить на части, как большинство предметов (например, разрезов яблоко пополам).
Само слово «naturalis» в переводе с латинского означает «естественный».
Если число не является ни дробным, ни отрицательным, то его можно назвать натуральным.
Натуральными числами люди пользуются уже много тысячелетий. Просто у разных народов были разные системы исчисления. Например, римляне для счета использовали палочки. Так и появились знаменитые римские цифры – I, V, X, L, C, D и M.
А вот в Древнем Вавилоне использовали шестеричную систему. И до наших дней она дошла в виде часов, в которых 1 час равен 60 минутам, а 1 минута равна 60 секундам.
И наконец, современное обозначение цифр (0, 1, 2, 3, 4, 5 и так далее) принадлежит арабам, хотя за основу они взяли индийскую десятеричную систему и добавили к ней «ноль».
Натуральный ряд
Если расположить натуральные числа в порядке возрастания, то полученная цепочка будет называться натуральным рядом.
Он всегда появляется, когда нам нужно что-то посчитать поштучно. Например, в магазине мы обычно так делаем с овощами или фруктами, берем 5 морковок или 3 яблока. А уже только потом взвешиваем их, так как цены указаны за килограмм.
И конечно, именно так учатся считать школьники в первом классе. Например, если в задачке нарисовано пять флажков и вопрос звучит «сколько?», то любой ребенок будет считать «пальцем», отмечая каждый флажок и озвучивая натуральный ряд «один, два, три, четыре, пять».
Ну и тут же будет важным упомянуть, что количество натуральных чисел бесконечно. А значит, и натуральный ряд является бесконечным.
Это записано в основном законе натуральных чисел:
Каким бы большим не было натуральное число N, всегда найдется натуральное число N+1, которое будет больше.
Ноль — это натуральное число или нет
Натуральный ряд можно построить двумя способами:
Вы спросите, в чем разница? Во втором случае возможен вариант, когда нужного предмета может и не быть вовсе. И тогда его количество равно нулю.
То есть натуральный ряд начинается не с единицы, а с ноля. И выглядит вот так: 0, 1, 2, 3, 4, 5 и так далее.
Соответственно, в первом случае ноль нельзя считать натуральным числом. А во втором – можно. Интересно, что споры, какой подход более правильный, у математиков идут до сих пор. И сторонников обеих теорий примерно поровну.
Но у российских школьников проблем с выбором нет. В нашей стране придерживаются той версии, что ноль – это натуральное число.
Операции с натуральными числами
Школьники в младших классах на уроках математики имеют дело только с натуральными числами. Помимо самих цифр учатся и самым простым действиям:
Вот и все, что мы хотели рассказать о натуральных числах.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
А стоит ли себе забивать голову, какое число натуральное, а какое нет? Мир от этого не станет, ни проще, ни сложнее. Да и что неестественного в отрицательных числах? Если человеку не хватает денег, чтобы рассчитаться с долгами, то его имущество как раз уйдет в минус, отдал за долги всё, что было, но остался должен, значит необходимо ещё заработать, чтоб из минуса выйти в ноль.
Натуральные числа
Натуральные числа — это числа, которые используются при счёте или нумерации.
Натуральные числа, записанные в порядке их возрастания (начиная с 1) и без пропусков, образуют ряд натуральных чисел, или короче натуральный ряд:
В натуральном ряду есть первое число — 1 (один или единица), но нет последнего числа — за каждым натуральным числом следует ещё одно, которое больше предшествующего на единицу. Таким образом, есть наименьшее натуральное число — 1, а наибольшего натурального числа не существует. Следовательно 1 — это самое маленькое натуральное число.
Натуральный ряд бесконечен.
Все натуральные числа записать невозможно. Поэтому при записи натурального ряда выписывают подряд несколько первых чисел, следующих друг за другом в натуральном ряду, и в конце ставят многоточие (три точки).
Отсутствие предметов для счёта условились обозначать числом 0 (нуль).
Нуль не считается натуральным числом.
Чётные и нечётные натуральные числа
В натуральном ряду чередуются нечётные и чётные числа, то есть числа, которые делятся на 2 и которые на 2 не делятся. Начинается натуральный ряд с нечётного числа:
Нечётные числа обозначены чёрным цветом, а чётные — красным.
Прямой и обратный счёт
Прямой счёт — это перечисление чисел в порядке их возрастания. Под порядком возрастания, в данном случае, подразумевается что каждое последующее число больше предыдущего на единицу.
Рассмотрим прямой счёт от 1 до 10:
| 1, | 2, | 3, | 4, | 5, | 6, | 7, | 8, | 9, | 10 |
| один | два | три | четыре | пять | шесть | семь | восемь | девять | десять |
Перечисление чисел натурального ряда в порядке их возрастания называется прямым счётом.
Обратный счёт — это перечисление чисел в порядке их убывания. Под порядком убывания, в данном случае, подразумевается что каждое последующее число меньше предыдущего на единицу.
Рассмотрим обратный счёт от 10 до 1:
| 10, | 9, | 8, | 7, | 6, | 5, | 4, | 3, | 2, | 1 |
| десять | девять | восемь | семь | шесть | пять | четыре | три | два | один |
Перечисление чисел натурального ряда в порядке их убывания называется обратным счётом.