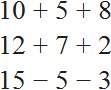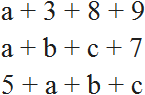Найди значение выражения что это значит
Значение числового, буквенного выражения и выражения с переменными.
При изучении темы числовые, буквенные выражения и выражения с переменными необходимо уделить внимание понятию значение выражения. В этой статье мы ответим на вопрос, что такое значение числового выражения, и что называют значением буквенного выражения и выражения с переменными при выбранных значениях переменных. Для разъяснения этих определений приведем примеры.
Навигация по странице.
Что называют значением числового выражения?
Знакомство с числовыми выражениями начинается чуть ли не с первых уроков математики в школе. Практически сразу вводится и понятие «значение числового выражения». Его относят к выражениям, составленным из чисел, соединенных знаками арифметических действий (+, −, ·, :). Дадим соответствующее определение.
Значение числового выражения – это число, которое получается после выполнения всех действий в исходном числовом выражении.
Часто в словосочетании «значение числового выражения» слово «числового» опускают, и говорят просто «значение выражения», так как все равно понятно, о значении какого выражения идет речь.
Часто на практике интерес представляет не столько числовое выражение, как его значение. То есть, встает задача, заключающаяся в определении значения данного выражения. При этом обычно говорят, что нужно найти значение выражения. В указанной статье подробно разобран процесс нахождения значения числовых выражений различного вида, и рассмотрена масса примеров с детальными описаниями решений.
Значение буквенного выражения и выражения с переменными
Помимо числовых выражений изучают буквенные выражения, то есть выражения, в записи которых вместе с числами присутствует одна или несколько букв. Буквы в буквенном выражении могут обозначать различные числа, и если буквы заменить этими числами, то буквенное выражение станет числовым.
Числа, которыми заменяют буквы в буквенном выражении, называют значениями этих букв, а значение полученного при этом числового выражения называют значением буквенного выражения при данных значениях букв.
Итак, для буквенных выражений говорят не просто о значении буквенного выражения, а о значении буквенного выражения при данных (заданных, указанных и т.п.) значениях букв.
В старших классах при изучении алгебры буквам в буквенных выражениях позволяют принимать различные значения, такие буквы называют переменными, а буквенные выражения – выражениями с переменными. Для этих выражений вводится понятие значения выражения с переменными при выбранных значениях переменных. Разберемся, что это такое.
Значением выражения с переменными при выбранных значениях переменных называется значение числового выражения, которое получается после подстановки выбранных значений переменных в исходное выражение.
Остается лишь добавить, что существуют выражения с переменными, значения которых не зависят от значений входящих в них переменных. Например, значение выражения с переменной x вида 2+x−x не зависит от значения этой переменной, оно равно 2 при любом выбранном значении переменной x из области ее допустимых значений, которая в данном случае является множеством всех действительных чисел.
Числовые и буквенные выражения
Числовые выражения
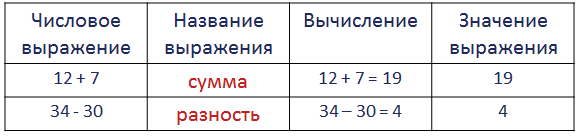
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
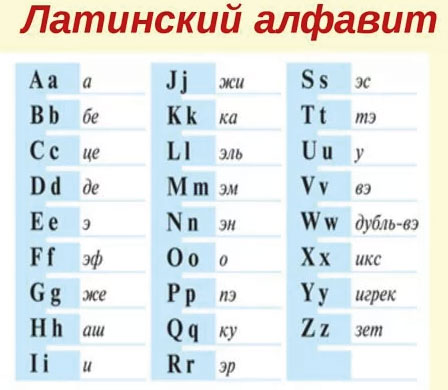
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
Значение переменной a подставляется в исходное выражение.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
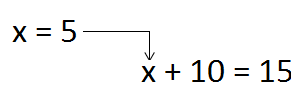
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b
Решение:
Значение выражения
Фраза « выполнить действие » означает выполнить одну из операций действия.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Пример 1. Значение числового выражения
Выполним сначала умножение и деление. Получаем:
Теперь проводим вычитание и получаем окончательный результат:
Сначала выполняем преобразование дробей, деление и умножение:
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Сначала вычисляем подкоренные выражения.
Теперь можно вычислить значение всего выражения.
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Начинаем вычислять по порядку.
Осталось только провести операцию сложение и узнать значение выражения:
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
Перепишем наше выражение и вычислим его значение:
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
Исходное выражение принимает вид:
Вычислим значение этого выражения:
Выражения с логарифмами
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
По свойству логарифмов:
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
Теперь можно переходить к вычислению значения исходного выражения.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
Подставляем значения в выражение и вычисляем его значение:
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
Пример 14. Значение числового выражения
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π
Теперь можно узнать значение синуса:
Вычисляем значение подкоренного выражения:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4
Со знаменателем дроби все проще:
Теперь мы можем записать значение всей дроби:
С учетом этого, запишем все выражение:
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Подставляем значения переменных в выражение и вычисляем:
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Еще один пример. Значение выражения x x равно единице для всех положительных иксов.