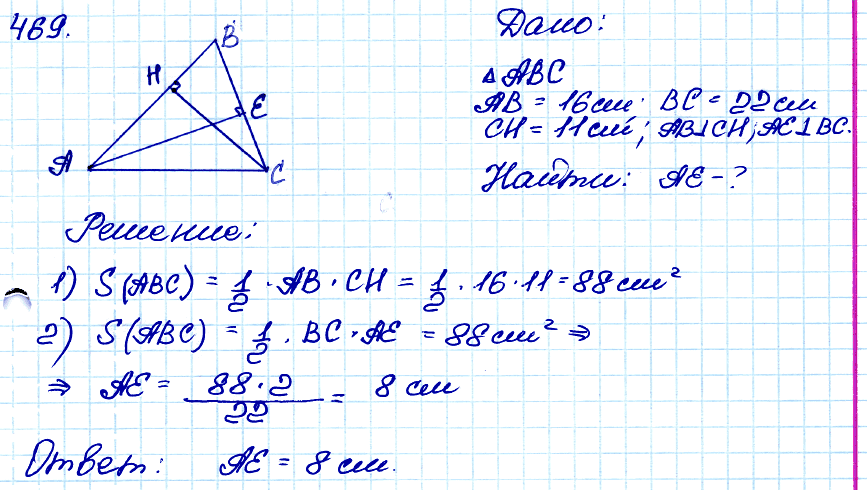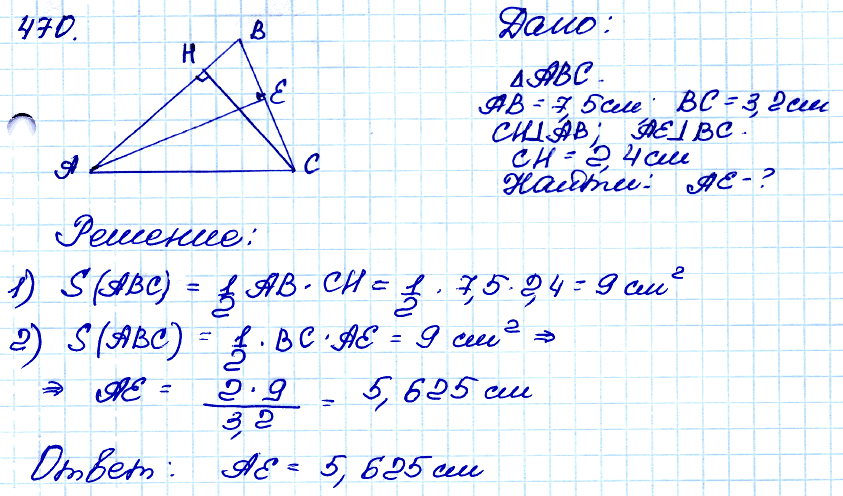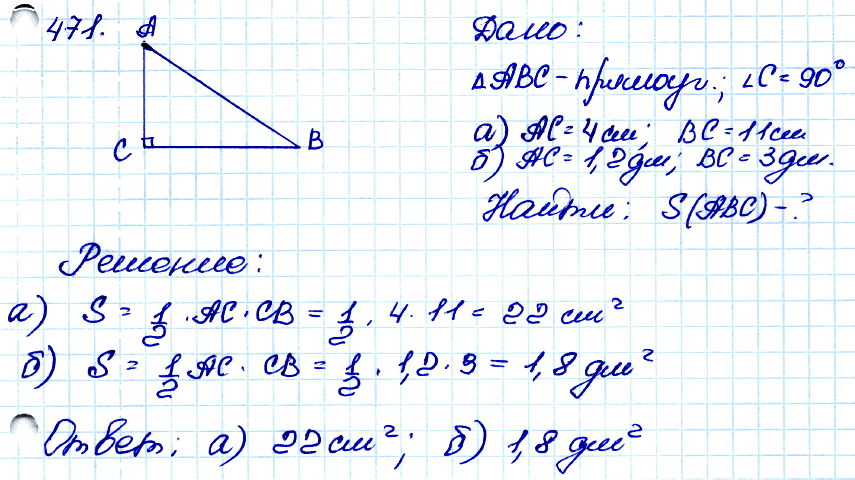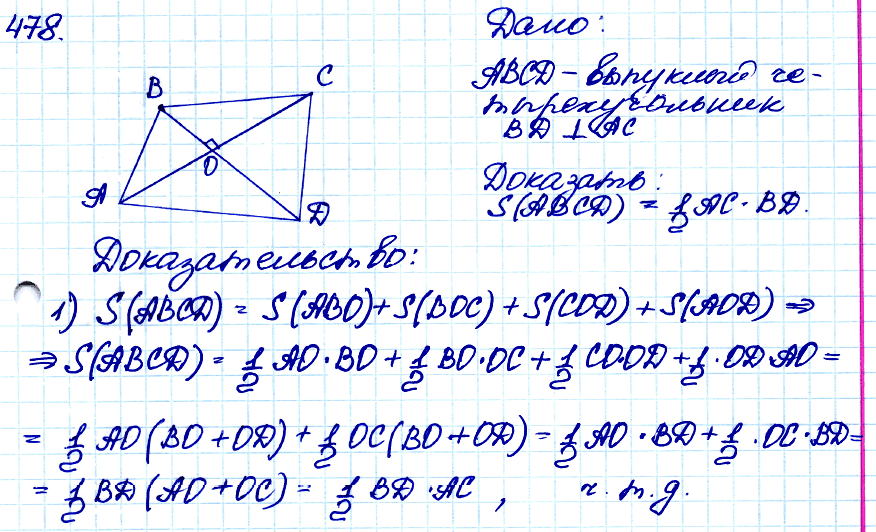Найдите углы треугольника если известно что площадь s этого треугольника

Геометрия 8 класс Атанасян Задачи 459-482

Упражнения 459-482 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.

Нажмите на спойлер, чтобы посмотреть ответ на задание.

Геометрия Атанасян. Глава 6.
§ 2. Площади параллелограмма,
треугольника и трапеции
Задачи №№ 459-482:

Задача № 460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.

Задача № 461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.

Задача № 462. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.

Задача № 463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма.

Задача № 465. Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.

Задача № 466. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если большая его сторона равна 15,2 см, а один из его углов 45°.

Задача № 467. Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.

Задача № 469. Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведённая к стороне АВ, равна 11 см. Найдите высоту, проведённую к стороне ВС.

Задача № 470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведённая к большей стороне, равна 2,4 см. Найдите высоту, проведённую к меньшей из данных сторон.

Задача № 471. □ Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11 см; б) 1,2 дм и 3 дм.

Задача № 473. Через вершину С треугольника АВС проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.

Задача № 474. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.

Задача № 475. □ Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.

Задача № 476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм и 14 см; б) 4,6 дм и 2 дм.

Задача № 478. В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.

Задача № 480. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 21 см, CD = 17 см, высота ВН равна 7 см;
б) ∠D = 30°, АВ = 2 см, CD = 10 см, DA = 8 см;
в) ВС ⊥ АВ, АВ = 5 см, ВС = 8 см, CD = 13 см.

Задача № 481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.

Задача № 482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведённая из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.

Источник

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

.

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:

.

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Источник

Как найти площадь треугольника

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Формула площади треугольника

Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.

Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.

Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!

Общая формула

1. Площадь треугольника через основание и высоту

, где — основание, — высота.

2. Площадь треугольника через две стороны и угол между ними

3. Площадь треугольника через описанную окружность и стороны

4. Площадь треугольника через вписанную окружность и стороны

Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:

5. Площадь треугольника по стороне и двум прилежащим углам

, где — сторона, и — прилежащие углы.

6. Формула Герона для вычисления площади треугольника

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

Для прямоугольного треугольника

Площадь треугольника с углом 90° по двум сторонам

Площадь треугольника по гипотенузе и острому углу

, где — гипотенуза, — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу

, где — катет, — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.

Площадь треугольника через гипотенузу и радиус вписанной окружности

, где — гипотенуза, — радиус вписанной окружности.

Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу

Площадь прямоугольного треугольника по формуле Герона

Для равнобедренного треугольника

Вычисление площади через основание и высоту

, где — основание, — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними

, где — боковая сторона, — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности

, где — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности

, где — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону

Площадь равностороннего треугольника через высоту

Таблица формул нахождения площади треугольника

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.

Источник

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Источник

Найдите углы треугольника если известно что площадь s этого треугольника

Загрузка решений доступна для зарегистрировавшихся пользователей

В остроугольном треугольнике ABC проведены высоты AP и CQ.

а) Докажите, что угол PAC равен углу PQC.

б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ABC = 60°.

Загрузка решений доступна для зарегистрировавшихся пользователей

В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и ∠KMN = 45°.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка О — центр окружности, вписанной в треугольник ABC. На продолжении отрезка AO за точку О отмечена точка K так, что BK = OK.

а) Докажите, что четырехугольник ABKC вписанный.

б) Найдите длину отрезка AO, если известно, что радиусы вписанной и описанной окружностей треугольника ABC равны 3 и 12 соответственно, а OK = 5.

Загрузка решений доступна для зарегистрировавшихся пользователей

В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 12, BC = 5. Окружность радиуса с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.

а) Докажите, что радиус второй окружности меньше, чем длины катета AC.

б) Найдите радиус второй окружности.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.

а) Докажите, что отрезок BK втрое больше отрезка CK.

б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 18 и BN = 17.

Загрузка решений доступна для зарегистрировавшихся пользователей

а) Докажите, что треугольник ABC прямоугольный.

Загрузка решений доступна для зарегистрировавшихся пользователей

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите расстояние между центрами его вписанной и описанной окружностей, если известно, что R = 4.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.

а) Докажите, что прямые AD и MC параллельны.

б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD= R.

а) Докажите, что треугольник ABC прямоугольный.

б) Вписанная окружность касается сторон AB и BC в точках E и F. Найдите площадь треугольника BEF, если известно, что R= 5 и CD =15.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD = R.

а) Докажите, что треугольник ABC прямоугольный.

б) Вписанная окружность касается сторон AB и BC в точках E и F. Найдите площадь треугольника BEF, если известно, что R = 2 и CD = 10.

Загрузка решений доступна для зарегистрировавшихся пользователей

Около остроугольного треугольника ABC описана окружность с центром O. На продолжении отрезка AO за точку O отмечена точка K так, что BAC + AKC=90°.

а) Докажите, что четырёхугольник OBKC вписанный.

б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если а

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность с центром O, вписанная в треугольник ABC, касается стороны BC в точке P и пересекает отрезок BO в точке Q. При этом отрезки OC и QP параллельны.

а) Докажите, что треугольник ABC ― равнобедренный.

б) Найдите площадь треугольника BQP, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2a.

Загрузка решений доступна для зарегистрировавшихся пользователей

Около равнобедренного треугольника ABC с основанием BC описана окружность. Через точку C провели прямую, параллельную стороне AB. Касательная к окружности, проведённая в точке B, пересекает эту прямую в точке K.

а) Докажите, что треугольник BCK — равнобедренный.

б) Найдите отношение площади треугольника ABC к площади треугольника BCK, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A. Вторая окружность с центром O₁ касается основания ML и продолжений боковых сторон.

а) Докажите, что треугольник OLO₁ прямоугольный.

б) Найдите радиус второй окружности, если известно, что радиус первой равен 6 и AK = 16.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что

а) Докажите, что точка I лежит на окружности, описанной около треугольника BOC.

б) Найдите угол OIH, если

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.

а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.

б) Найдите если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точки A₁, B₁ и C₁ — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.

а) Докажите, что отличная от A₁ точка пересечения окружностей, описанных около треугольников A₁CB₁ и A₁BC₁, лежит на окружности, описанной около треугольника B₁AC₁.

б) Известно, что AB = AC = 10 и BC = 12. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры окружностей, описанных около треугольников A₁CB₁, A₁BC₁ и B₁AC₁.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.

а) Докажите, что треугольник ABC равнобедренный.

б) Найдите, в каком отношении высота этого треугольника делит сторону BC.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC точки A₁, B₁ и C₁ — середины сторон BC, AC и AB соответственно, AH — высота,

б) Найдите A₁H, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка M — середина гипотенузы AB прямоугольного треугольника ABC. Серединный перпендикуляр к гипотенузе пересекает катет BC в точке N.

а) Докажите, что ∠CAN = ∠CMN.

б) Найдите отношение радиусов окружностей, описанных около треугольников ANB и CBM, если

Загрузка решений доступна для зарегистрировавшихся пользователей

В прямоугольном треугольнике ABC проведена высота CH из вершины прямого угла. В треугольники ACH и BCH вписаны окружности с центрами O₁ и O₂ соответственно, касающиеся прямой CH в точках M и N соответственно.

а) Докажите, что прямые AO₁ и CO₂ перпендикулярны.

б) Найдите площадь четырёхугольника MO₁NO₂, если AC = 20 и BC = 15.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.

а) Докажите, что AD = 4BC.

б) Найдите длину отрезка MN, если радиус окружности равен

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность с центром O, вписанная в треугольник ABC, касается его сторон BC, AB и AC в точках K, L и M соответственно. Прямая KM вторично пересекает в точке P окружность радиуса AM с центром A.

а) Докажите, что прямая AP параллельна прямой BC.

Загрузка решений доступна для зарегистрировавшихся пользователей

Угол BAC треугольника ABC равен Сторона BC является хордой такой окружности с центром O и радиусом R, которая проходит через центр окружности, вписанной в треугольник ABC.

а) Докажите, что около четырёхугольника ABOC можно описать окружность.

б) Известно, что в четырёхугольник ABOC можно вписать окружность. Найдите радиус r этой окружности, если R = 6,

Загрузка решений доступна для зарегистрировавшихся пользователей

Вневписанная окружность равнобедренного треугольника касается его боковой стороны.

а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на его основание.

б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка I — центр окружности S₁, вписанной в треугольник ABC, точка O — центр окружности S₂, описанной около треугольника BIC.

а) Докажите, что точка O лежит на окружности, описанной около треугольника ABC.

б) Найдите косинус угла BAC, если радиус описанной окружности треугольника ABC относится к радиусу окружности S₂ как 3:5.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка O — центр окружности, описанной около остроугольного треугольника ABC, а BH — высота этого треугольника.

а) Докажите, что углы ABH и CBO равны.

б) Найдите BH, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка O — центр окружности, описанной около остроугольного треугольника ABC, а BH — высота этого треугольника.

а) Докажите, что углы ABH и CBO равны.

б) Найдите BH, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан треугольник ABC со сторонами и Точки M и N — середины сторон AB и AC соответственно.

а) Докажите, что окружность, вписанная в треугольник ABC, касается одной из средних линий.

б) Найдите общую хорду окружностей, одна из которых вписана в треугольник ABC, а вторая описана около треугольника AMN.

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан треугольник ABC со сторонами AC = 30, BC = 40 и AB = 50. Вписанная в него окружность с центром I касается стороны BC в точке L, M — середина BC, AP — биссектриса треугольника ABC, O — центр описанной около него окружности.

а) Докажите, что P — середина отрезка LM.

б) Пусть прямые OI и AC пересекаются в точке K, а продолжение биссектрисы AP пересекает описанную окружность в точке Q. Найдите площадь четырёхугольника OKCQ.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC биссектрисы AD и CE пересекаются в точке O, величина угла AOC составляет 120°.

а) Докажите, что около четырехугольника BDOE можно описать окружность.

б) Найдите площадь треугольника ABC, если а

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность с центром O, вписанная в треугольник ABC, касается стороны BC в точке K. К этой окружности проведена касательная, параллельная биссектрисе AP треугольника и пересекающая стороны AC и BC в точках M и N соответственно.

а) Докажите, что угол MOC равен углу NOK.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность, вписанная в треугольник ABC, касается сторон BC и AC в точках M и N соответственно, E и F — середины сторон AB и AC соответственно. Прямые MN и EF пересекаются в точке D.

а) Докажите, что треугольник DFN равнобедренный.

б) Найдите площадь треугольника BED, если AB = 20 и ∠ABC = 60°.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность, касающаяся сторон AB и BC треугольника ABC, пересекает сторону AC в точках M и P, причем

а) Докажите, что треугольник ABC — равнобедренный.

б) Найдите радиус окружности, если а центр окружности лежит на высоте к стороне BC.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC биссектриса угла B пересекает описанную окружность этого треугольника в точке F. Точка E — центр окружности, касающейся стороны АС и продолжений сторон AB и BC (вневписанной окружности). Точка O — центр вписанной окружности треугольника ABC.

а) Докажите, что отрезки AF и OF равны.

б) Найдите длину отрезка CF, если OE = 14.

Загрузка решений доступна для зарегистрировавшихся пользователей

Вписанная в треугольник ABC окружность с центром O касается сторон AB и AC в точках M и N соответственно. Прямая BO пересекает окружность, описанную около треугольника CON вторично в точке P.

а) Докажите, что точка P лежит на прямой MN.

б) Найдите площадь треугольника ABP, если площадь треугольника ABC равна 24.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC проведены биссектрисы BM и CN. Оказалось, что точки B, C, M и N лежат на одной окружности.

а) Докажите, что треугольник ABC равнобедренный.

б) Пусть P — точка пересечения биссектрис треугольника ABC. Найдите площадь четырёхугольника AMPN, если MN : BC = 2 : 5, а BN = 14.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность проходит через вершины B и C треугольника ABC и пересекает AB и AC в точках C₁ и B₁ соответственно.

а) Докажите, что треугольник ABC подобен треугольнику AB₁C₁.

б) Найдите радиус данной окружности, если ∠A = 45°, B₁C₁ = 6 и площадь треугольника AB₁C₁ в восемь раз меньше площади четырёхугольника BCB₁C₁.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC проведена биссектриса BK.

а) Докажите, что

б) Найдите площадь треугольника ABC, если AB = 13, BC = 7 и

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольник ABC вписана окружность радиуса 4, касающаяся стороны AC в точке M, причём AM = 8 и CM = 12.

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите расстояние между центрами вписанной и описанной окружностей треугольника ABC.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С₁ и В₁ соответственно.

а) Докажите, что треугольник АВC подобен треугольнику АВ₁С₁

б) Вычислите радиус данной окружности, если и площадь треугольника АВ₁С₁ в четыре раза меньше площади четырёхугольника ВСВ₁С₁.

Загрузка решений доступна для зарегистрировавшихся пользователей

Две окружности касаются внутренним образом в точке С. Вершины A и B равнобедренного прямоугольного треугольника ABC c прямым углом C лежат на большей и меньшей окружностях соответственно. Прямая AC вторично пересекает меньшую окружность в точке D. Прямая BC вторично пересекает большую окружность в точке E.

а) Докажите, что AE параллельно BD.

б) Найдите AC, если радиусы окружностей равны 8 и 15.

Загрузка решений доступна для зарегистрировавшихся пользователей

Прямоугольный треугольник ABC с прямым углом C вписан в окружность. Биссектриса угла A пересекает описанную окружность в точке A₁, биссектриса угла B пересекает описанную окружность в точке B₁, биссектриса угла C пересекает описанную окружность в точке C₁.

б) Известно, что Найдите B₁C₁.

Загрузка решений доступна для зарегистрировавшихся пользователей

В остроугольном треугольнике ABC провели высоту CC₁ и медиану AA₁. Оказалось, что точки A, A₁, C, C₁ лежат на одной окружности.

а) Докажите, что треугольник ABC равнобедренный.

Загрузка решений доступна для зарегистрировавшихся пользователей

В прямоугольный треугольник АВС с катетами АС = 4, ВС = 3 вписана окружность с центром О, касающаяся сторон ВС, АС и АВ треугольника в точках R, Q, P соответственно.

а) Докажите, что AO · BO · CO = 10.

б) Найдите площадь треугольника PQR.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка О₁ — центр вписанной окружности равнобедренного треугольника АВС, а точка О₂ — центр вневписанной окружности, касающейся основания ВС.

а) Докажите, что расстояние от середины отрезка О₁О₂ до точки С вдвое меньше О₁О₂.

б) Известно, что радиус первой окружности в пять раз меньше радиуса второй. В каком отношении точка касания первой окружности с боковой стороной треугольника делит эту сторону?

Загрузка решений доступна для зарегистрировавшихся пользователей

В остроугольном треугольнике АВС провели высоты АН₁ и СН₂, затем провели луч НМ, который пересекает окружность, описанную около треугольника АВС, в точке К, где М — середина АС, а Н — точка пересечения высот.

а) Докажите, что НМ = МК.

б) Найдите площадь треугольника ВСК, если AC = 1.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность с центром О, вписанная в треугольник АВС, касается его сторон ВС, АВ и АС в точках K, L и М соответственно. Прямая КМ вторично пересекает в точке Р окружность радиуса АМ с центром А.

а) Докажите, что прямая АР параллельна прямой ВС.

б) Пусть AM = 3, CM = 2, Q — точка пересечения прямых КМ и АВ, а Т — такая точка на отрезке РQ, что Найдите QT.

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан прямоугольный треугольник АВС с прямым углом С. На катете АС взята точка М. Окружность с центром О и диаметром СМ касается гипотенузы в точке N.

а) Докажите, что прямые MN и ВО параллельны.

б) Найдите площадь четырехугольника BOMN, если CN = 8, AM : MC = 1 : 3.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC AB = 3, Хорда KN окружности, описанной около треугольника ABC, пересекает отрезки AC и BC в точках M и L соответственно. Известно, что площадь четырёхугольника ABLM равна 2, LM = 1.

а) Докажите, что треугольник KNC равнобедренный.

б) Найдите площадь треугольника KNC.

Загрузка решений доступна для зарегистрировавшихся пользователей

В остроугольном треугольнике ABC высоты BB₁ и CC₁ пересекаются в точке H.

а) Докажите, что

б) Найдите расстояние от центра описанной окружности треугольника ABC до стороны BC, если B₁C₁ = 12 и

Загрузка решений доступна для зарегистрировавшихся пользователей

В окружности с центром O проведена хорда AB, на которой выбрана точка M. Вторая окружность, описанная около треугольника MAO, повторно пересекает первую окружность в точке K.

а) Докажите, что BM = MK.

б) Найдите площадь треугольника OMK, если OM = 11 и BK = 12.

Загрузка решений доступна для зарегистрировавшихся пользователей

б) Найдите площадь четырёхугольника ACBM, если дополнительно известно, что площадь треугольника BCM равна 24.

Загрузка решений доступна для зарегистрировавшихся пользователей

В каждый угол равнобедренного треугольника ABC, в котором вписана окружность единичного радиуса, точки О₁, О₂ и О₃ центры этих окружностей. Найдите:

а) радиус окружности, вписанной в треугольник ABC;

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике АВС известно, что АВ = АС = 10, ВС = 12. На стороне АВ отметили точки М₁ и М₂ так, что AM₁

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC биссектриса угла A пересекает сторону BC в точке D. Окружность, описанная около треугольника ACD пересекает сторону AB в точке E.

а) Докажите, что треугольник CDE равнобедренный.

б) Найдите площадь треугольника CDE, если AB = 8, BC = 7, AC = 6.

Загрузка решений доступна для зарегистрировавшихся пользователей

На окружности с центром O и диаметром MN, равным 34, взята точка K на расстоянии 15 от этого диаметра. Хорда KE пересекает радиус OM в точке F под углом, равным

а) Докажите, что KF : FE = 125 : 29.

б) Найдите площадь треугольника KEN.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точки D и E — середины сторон AC и BC треугольника ABC соответственно. На отрезке DE как на диаметре построена окружность, пересекающая продолжения сторон AC и BC в точках M и N соответственно.

а) Докажите, что биссектрисы углов MEN и NDM пересекаются на этой окружности.

б) Найдите MN, если известно, что AB = 14, BC = 10, AC = 6.

Загрузка решений доступна для зарегистрировавшихся пользователей

Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H. Отрезок AP — диаметр окружности, описанной около треугольника ABC.

а) Докажите, что прямая HP пересекает отрезок BC в его середине.

б) Луч PH вторично пересекает окружность, описанную около треугольника ABC, в точке M. Найдите длину отрезка MC₁, если расстояние от центра этой окружности до прямой BC равно 4, ∠BPH = 120°.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность, вписанная в треугольник ABC, делит медиану BM на три равные части.

а) Докажите, что BC : CA : AB = 5 : 10 : 13.

б) Найдите радиус вписанной окружности, если BM = 12.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность, проходящая через вершину B треугольника ABC, касается стороны AC в точке D, такой, что BD — биссектриса угла B, и пересекает стороны AB и BC в точках E и F соответственно.

б) Найдите отношение площадей треугольников AED и DFC, если известно, что AE : CF = 2 : 3.

Загрузка решений доступна для зарегистрировавшихся пользователей

Треугольник ABC прямоугольный с прямым углом C. Проведена высота CH. На сторонах AC и BC соответственно отмечены точки M и N так, что угол MHN прямой.

а) Докажите, что треугольники MNH и ABC подобны.

б) Найдите BN, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Треугольник ABC прямоугольный с прямым углом C. Проведена высота CH. На сторонах AC и BC соответственно отмечены точки M и N так, что угол MHN прямой.

а) Докажите, что треугольники MNH и ABC подобны.

б) Найдите BN, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Отрезок CH — высота прямоугольного треугольника ABC с прямым углом C. На катетах AC и BC выбраны точки M и N соответственно такие, что

a) Докажите, что треугольник MNH подобен треугольнику ABC.

б) Найдите CN, если BC = 3, AC = 5, CM = 2.

Загрузка решений доступна для зарегистрировавшихся пользователей

Окружность с центром О, построенная на катете AC прямоугольного треугольника ABC как на диаметре, пересекает гипотенузу AB в точках A и D. Касательная проведенная к этой окружности в точке D, пересекает катет BC в точке M.

а) Докажите, что BM = CM.

б) Прямая DM пересекает прямую AC в точке P, прямая OM пересекает прямую BP в точке K. Найдите если

Загрузка решений доступна для зарегистрировавшихся пользователей

На стороне KM остроугольного треугольника PKM (PK ≠ PM) как на диаметре построена полуокружность, пересекающая высоту PS в точке T, PS = 8, TS = 6, H — точка пересечения высот треугольника PKM.

б) Полуокружность пересекает стороны PK и PM в точках L и N соответственно. Найдите коэффициент подобия треугольников PKM и PNL, если радиус полуокружности равен 20.

Загрузка решений доступна для зарегистрировавшихся пользователей

Высота BH треугольника ABC в раз больше радиуса описанной около треугольника ABC окружности с центром O.

а) Доказать, что прямая, проходящая через точки K и M — основания перпендикуляров, опущенных из точки H на стороны AB и BC соответственно, проходит через точку O.

б) Найдите радиус описанной около треугольника ABC окружности, если AB = 6,

Загрузка решений доступна для зарегистрировавшихся пользователей

Источник