Найдите вероятность того что при подбрасывании кубика выпадет четное число очков
Решение задач о бросании игральных костей
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Одна игральная кость
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
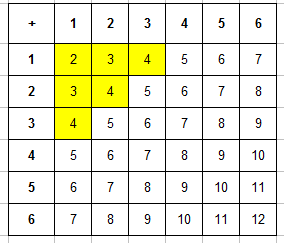
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
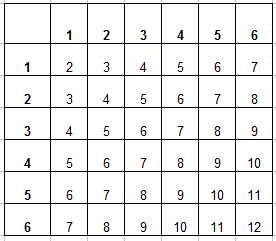
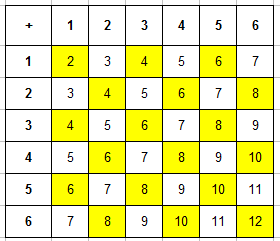
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
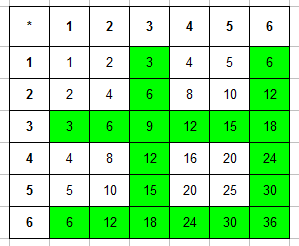
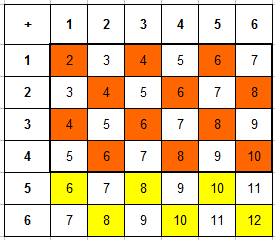
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.
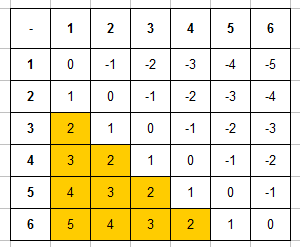
Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:
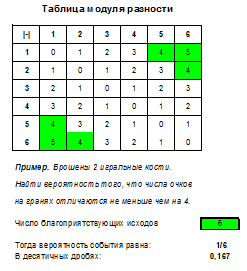
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).
Другие задачи про кости и кубики
Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.
Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.
В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.
Теперь подберем такие исходы, которые дают в сумме 15 очков.
Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.
Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.
В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.
Приведем еще пример, решаемый аналогичным образом.
Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.
Полезные ссылки
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.
В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.
Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.
Еще по теории вероятностей:
В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):
Вероятность игральной кости.
Задачи на вероятность игральной кости не менее популярны, чем задачи о подбрасывании монет. Условие такой задачи обычно звучит так: при бросании одной или нескольких игральных костей (2 или 3), какова вероятность того, что сумма очков будет равна 10, или число очков равно 4, или произведение числа очков, или делится на 2 произведение числа очков и так далее.
Применение формулы классической вероятности является основным методом решения задач такого типа.
Одна игральная кость, вероятность.
Задача 1. Один раз брошена игральная кость. Какова вероятность выпадения четного числа очков?
Поскольку игральная кость собой представляет кубик (или его еще называют правильной игральной костью, на все грани кубик выпадет с одинаковой вероятностью, так как он сбалансированный), у кубика 6 граней (число очков от 1 до 6, которые обычно обозначаются точками), это значит, что в задаче общее число исходов: n=6. Событию благоприятствуют только исходы, при которых выпадает грань с четными очками 2,4 и 6, у кубика таких граней: m=3. Теперь можем определить искомую вероятность игральной кости: P=3/6=1/2=0.5.
Задача 2. Брошен один раз игральный кубик. Какова вероятность, что выпадет не менее 5 очков?
Решается такая задача по аналогии с примером, указанным выше. При бросании игрального кубика общее число равновозможных исходов равно: n=6, а удовлетворяют условие задачи (выпало не менее 5 очков, то есть выпало 5 или 6 очков) только 2 исхода, значит m=2. Далее находим нужную вероятность: P=2/6=1/3=0.333.
Две игральные кости, вероятность.
Задача 3. Брошены одновременно 2 игральные кости. Какова вероятность выпадения суммы менее 5 очков?
Теперь можно заполнить таблицу, для этого в каждую ячейку заносится число суммы очков, которые выпали на первой и второй кости. Заполненная таблица выглядит так:
Благодаря таблице определим число исходов, которые благоприятствуют событию » выпадет в сумме менее 5 очков». Произведем подсчет числа ячеек, значение суммы в которых будет меньше числа 5 (это 2, 3 и 4). Такие ячейки для удобства закрашиваем, их будет m=6:
Учитывая данные таблицы, вероятность игральной кости равняется: P=6/36=1/6.
Задача 4. Было брошено две игральные кости. Определить вероятность того, что произведение числа очков будет делиться на 3.
Для решения задачи составим таблицу произведений очков, которые выпали на первой и на второй кости. В ней сразу же выделим числа кратные 3:
Записываем общее число исходов эксперимента n=36 (рассуждения такие же как в предыдущей задаче) и число благоприятствующих исходов (число ячеек, которые закрашены в таблице) m=20. Вероятность события равняется: P=20/36=5/9.
Задача 5. Дважды брошена игральная кость. Какова вероятность, что на первой и второй кости разность числа очков будет равна от 2 до 5?
Чтобы определить вероятность игральной кости запишем таблицу разностей очков и выделим в ней те ячейки, значение разности в которых будет между 2 и 5:
Число благоприятствующих исходов (число ячеек, закрашенных в таблице) равно m=10, общее число равновозможных элементарных исходов будет n=36. Определит вероятность события: P=10/36=5/18.
В случае простого события и при бросании 2-х костей, требуется построить таблицу, затем в ней выделить нужные ячейки и их число поделить на 36, это и будет считаться вероятностью.
Найдите вероятность того что при подбрасывании кубика выпадет четное число очков
Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.
При бросании кубика равновозможны шесть различных исходов. Событию «выпадет более трёх очков» удовлетворяют три случая: когда на кубике выпадает 4, 5 или 6 очков. Поэтому вероятность того, что на кубике выпадет более 3 очков равна 
Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет менее 4 очков.
При бросании кубика равновозможны шесть различных исходов. Событию «выпадет менее четырёх очков» удовлетворяют три случая: когда на кубике выпадает 1, 2 или 3 очка. Поэтому вероятность того, что на кубике выпадет менее 4 очков равна
Во время вероятностного эксперимента монету бросили 1000 раз, 532 раза выпал орел. На сколько частота выпадения решки в этом эксперименте отличается от вероятности этого события?
Всего возможны два исхода эксперимента, выпадению решки удовлетворяет один из них, поэтому вероятность выпадения решки в этом эксперименте равна 1 : 2 = 0,5. Частота выпадения решки в данном эксперименте равна (1000 − 532) : 1000 = 0,468. Поэтому частота выпадения решки в этом эксперименте отличается от вероятности этого события на 0,5 − 0,468 = 0,032.
Решение задач по теории вероятностей
Теория вероятностей ( для выполнения заданий ЕГЭ)
Купив лотерейный билет, мы можем выиграть, а можем и не выиграть; на очередных выборах правящая партия может победить, а может и не победить; завтра на уроке математики вас могут вызвать к доске, а могут и не вызвать.
Все это примеры случайных событий, которые при одних и тех же условиях могут произойти, а могут и не произойти.
Примеры случайных событий:
Если же событие при данных условиях обязательно произойдет, то его называют достоверным. Например:
Для лучшего понимания понятия «вероятность» приведём в качестве примера задачи:
Пусть ровно m из этих n исходов приводят к наступлению некоторого события А. Будем называть такие исходы благоприятными для этого события (они ему благоприятствуют, т. е. событие А наступает при любом из этих исходов).
Классическое определение вероятности
Вероятностью случайного события А назовем дробь m / n , где n — число всех возможных исходов эксперимента, m — число исходов, благоприятных для события А:
Следовательно, Р(А) = 18/36 = 1/2 = 0,5.
Совершенно аналогично находим число благоприятных исходов и вероятности для оставшихся событий:
для события С т = 0, Р(С) = 0/36 = 0;
для события D т = 4, Р( D ) = 4/36 = 1/9 =0,111;
для события Е т = 1, Р(Е) = 1/36 = 0,028.
№ 2. В двух коробках лежат карандаши одинаковой величины и формы, но разного цвета. В первой коробке 4 красных и 6 черных, а во второй 3 красных, 5 синих и 2 черных. Из обеих коробок вынимается наугад по одному карандашу. Какова вероятность того, Что оба карандаша окажутся красными?
Решение. Испытание состоит в том, что из каждой коробки » вынимается по одному карандашу. Пусть событие А означает, что вынутый карандаш из первой коробки оказался красным, событие
В — что вынутый карандаш из второй коробки тоже красный. Тогда событие АВ означает, что оба вынутые карандаша оказались красными. Поскольку события А и В независимы, то P (АВ) = P (А) P (В). Вероятности событий А и В равны соответственно P (А) = 0,4, P (В) = 0,3. Следовательно, вероятность того, что оба карандаша оказались красными, равна P (АВ) =
№ 3. Брошена игральная кость. Какова вероятность того, что выпадет четное число очков?
№ 4. Родительский комитет закупил 30 пазлов для подарков детям на окончание учебного года, из них 12 с персонажами мультфильмов и 18 с видами природы. Подарки распределяются случайным образом. Найдите вероятность того, что Маше достанется пазл с персонажем из мультфильма.
№ 5. На тарелке 15 пирожков: 6 с яблоками, 4 с капустой, 5 с печенью. Варя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с яблоками.
№ 6. На экзамене 40 билетов, Игорь не выучил 2 из них. Найдите вероятность того, что ему попадется выученный билет.
Решение: Число возможных исходов 40, число благоприятных исходов: 40-2=38.
Искомая вероятность равна: 38/40=0,95.
№ 7. При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что первый раз выпало меньше трех очков.
Сумму в 6 очков можно получить следующими способами ( переберем варианты):1+5,2+4,3+3,4+2,5+1 – всего их пять, это и есть число возможных исходов. Из представленных вариантов также видно, что менее трёх очков при первом броске может выпасть только в двух случаях. Искомая вероятность равна:2/5=0,4.
№ 8. Марина и Дина бросают кубик по одному разу. Выигрывает та девочка, у которой выпадет больше очков. Первой бросила Марина, у неё выпало 3 очка. Найдите вероятность того, что Дина выиграет.
Решение: Для того, что бы выиграть у Дины должно выпасть 4, 5 или 6 очков. Т. е. 3 благоприятных исхода из 6 – ти возможных (1,2,3,4,5 или 6). 3/6= 0,5.
Решение: Комбинации выпадения очков : 4:1, 4:2, 4:3, 4:4, 4:5, 4:6. Всего 6. Из них выигрышных для первого 3 (первые из перечисленных). Значит вероятность того, что он выиграет: 3/6=0,5.
№ 7. Монету бросают трижды. Найдите вероятность того, что первые два броска окончатся одинаково.
Решение: Найдем число возможных исходов, переберем все варианты бросков. В подобных задачах удобнее составит таблицу:
Всего возможных исходов восемь.
Первые два одинаково могут закончиться в четырех случаях, это 1,2,5,6 варианты, т.е. благоприятных исходов 4. Искомая вероятность равна: 4/8=0,5.
(Эту же задачу можно решить и при помощи произведения и суммы вероятностей, но в данном случае этот способ, по-моему, сложнее)
№ 8. Монету бросают трижды. Найдите вероятность того, что только первые два броска окончатся одинаково.
Решение: В этой формулировке благоприятных исходов будет уже только 2 ( 2 и 6 варианты). А всего исходов, как и в предыдущей задаче, будет 8. Искомая вероятность равна: 2/8=0,25.
№ 9. При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало меньше 3 очков.
Решение: 6 очком могло выпасть только при следующих раскладах: 1 и 5, 2 и 4, 3 и 3, 5 и 1, 4 и 2. Всего 5 возможных вариантов. В первый раз выпадает меньше 3 очков только в двух случаях. Вычислим искомую вероятность: 2/5=0,4.
№ 10. Найдите вероятность того, что при бросании двух кубиков на каждом выпадет менее 4 очков.
Решение: Всего возможных комбинаций будет 36. Из них благоприятными будут 9:
№ 11. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары с помощью жребия. Всего в чемпионате участвует 26 спортсменов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение: Выясним чему равно число исходов, а так же число благоприятных исходов. Всего спортсменов 26, включая Руслана, значит играть он сможет с кем-либо из оставшихся 25-ти. Т.о. число возможных исходов – 25. Среди оставшихся 25-ти спортсменов 9( Руслана не считаем) из России. Значит, благоприятных исходов – 9. Искомая вероятность равна: 9/25=0,36.
№ 12. В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября. Найдите вероятность того. Что будут дежурить два мальчика.
Решение: для каждого из 21- го ребенка может быть в паре один из оставшихся 20. Т.е. число возможных пар: 21*20=420. Благоприятными будут пары, когда для каждого из 7 мальчиков в пару попадет один из оставшихся 6-ти. Т.о. количество благоприятных исходов вычислим: 6*7=42.
Искомая вероятность: 42/420=0,1.
№ 13. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвуют 56 шашистов, среди которых 12 участников из России, в том числе и Валерий Стремянкин. Найдите вероятность того, что в первом туре Валерий Стремянкин будет играть с каким-либо шашистом из России.
Решение: Всего Валерий Стремянкин может играть с каким-либо из 55 (исключая его самого из общего количества) шашистов. Благоприятными для нас являются 11 исходов из них (Из России всего12 шашистов, 1 из них сам Стремянкин, значит соперников возможных у него 11). Находим исходную вероятность: 11/55=0,2.
№ 14. В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайным образом. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдет приз в своей банке.
Решение: В четырёх банках из пяти нет приза. Значит, исходная вероятность будет равна: 4/5=0,8.
№ 15. В среднем на 150 карманных фонариков приходится 3 неисправных. Какова вероятность купить исправных фонариков?
Количество возможных исходов 150. Количество благоприятных исходов: 150-3=147. Вероятность купить исправный фонарик 147 к 150: 147/150 = 0,98.
№ 16. В среднем на 150 исправных карманных фонариков приходится 3 неисправных. Какова вероятность купить исправный фонарик?
В этом случае число возможных исходов: 150+3=153 ( 150 исправных плюс 3 неисправных).
Число благоприятных исходов = 150 ( число исправных фонариков). Вероятность купить исправный фонарик равна: 150/153 = 50/51 ≈ 0,9804…
№ 17. Фабрика выпускает сумки. В среднем на 100 качественных приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение: Сказано, что на 100 качественных сумок приходится 8 с дефектом, значит число возможных исходов 100+8=108. Число благоприятных исходов 100(качественные сумки). Вероятность того, что купленная сумка окажется качественной, равна 1оо к 108: 100/108=0,9259…≈ 0, 93.
№ 18. Какая сумма, скорее всего, выпадет при бросании двух кубиков?
Решение: Возможные суммы : 1+1=2, 1+2=3, 1+3=4, 1+4=5, 1+5=6, 1+6=7,2+1=3, 2+2=4, 2+3=5, 2+4=6, 2+5=7, 2+6=8, 3+1=4, 3+2=5,3+3=6, 3+4=7,3+5=8,3+6=9, 4+1=5, 4+2=6, 4+3=7, 4+4=8, 4+5=9,4+6=10, 5+1=6, 5+2=7, 5+3=8, 5+4=9, 5+5=10,5+6=11, 6+1=7, 6+2=8,6+3=9, 6+4=10, 6+5=11, 6+6=12. Возможные суммы:
Чаще всего выпадает сумма 7.
№ 19. Валя выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 51.
Решение: Найдём количество всех трёхзначных чисел, делящихся на 51. Первое из них 102, далее 153 и т.д. Сколько будет таких чисел среди трёхзначных? 999: 51=19, 588…, т.е. чисел кратных 51 до 999 будет 19. Из них одно двузначное 51, значит 19-1=18. 18 трёхзначных чисел, делящихся на 51. А всего трёхзначных чисел : 999-99=900. Найдём искомую вероятность: 18/900=0,02.
Все вышеперечисленные задачи решались, опираясь на классическое определение вероятности.
Сборники заданий ЕГЭ предлагают так же ряд задач, решаемых при помощи произведения и сложения вероятностей.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на вероятность другого.
(Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, исчисленную в предположении, что первое событие уже произошло.
Условной вероятностью события В называется вероятность события В, найденная в предположении, что событие А уже наступило.)
Суммой событий А и В называется событие С=А+В, состоящее в наступлении, по крайней мере, одного из событий А или В, т. е. в наступлении события А, или события В, или обоих этих событий вместе, если они совместны.
Теорема. Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий: 
.
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий.
а) только одно отделение получит газеты вовремя;
б) хотя бы одно отделение получит газеты с опозданием.
Решение: Введем события
А1 = (газеты доставлены своевременно в первое отделение),
А2 = (газеты доставлены своевременно во второе отделение),
А3 = (газеты доставлены своевременно в третье отделение),
по условию P(A1)=0,95; P(A2) = 0,9; P(A3)=0,8.
Найдем вероятность события Х = (только одно отделение получит газеты вовремя). Событие Х произойдет, если
или газеты доставлены своевременно в 1 отделение, и доставлены не вовремя во 2 и 3,
или газеты доставлены своевременно в 2 отделение, и доставлены не вовремя во 1 и 3,
или газеты доставлены своевременно в 3 отделение, и доставлены не вовремя во 2 и 1.
Таким образом, 
Найдем вероятность события У=(хотя бы одно отделение получит газеты с опозданием). Введем противоположное событие = 
(все отделения получат газеты вовремя). Вероятность этого события
Тогда вероятность события У:
№ 21. В двух коробках лежат карандаши одинаковой величины и формы, но разного цвета. В первой коробке 4 красных и 6 черных, а во второй 3 красных, 5 синих и 2 черных. Из обеих коробок вынимается наугад по одному карандашу. Какова вероятность того, Что оба карандаша окажутся красными?
Решение. Испытание состоит в том, что из каждой коробки » вынимается по одному карандашу. Пусть событие А означает, что вынутый карандаш из первой коробки оказался красным, событие
В — что вынутый карандаш из второй коробки тоже красный. Тогда событие АВ означает, что оба вынутые карандаша оказались красными. Поскольку события А и В независимы, то P (АВ) = P (А) P (В). Вероятности событий А и В равны соответственно P (А) = 0,4, P (В) = 0,3. Следовательно, вероятность того, что оба карандаша оказались красными, равна P (АВ) =
№ 22. В случайном эксперименте монету бросают трижды. Найти вероятность того, что орел не выпадет ни разу.
Решение: Задачу можно решить, пользуясь классическим определением вероятности или теоремой о произведении вероятностей.
1 способ. Решим задачу, используя теорему о произведении вероятностей.
Орел не выпадет ни разу только в случае выпадения: решка, решка, решка. Вероятность выпадения решки в 1-ый раз =0,5 (1 из двух вариантов выпадения). Аналогично: вероятность выпадения решки во 2-ой раз=0,5. И в 3-ий раз тоже =0,5. Поскольку это вероятности зависимых событий, мы находим их произведение: 0,5*0,5*0,5=0,125.
2 способ. Решим задачу, используя классическое определение вероятности.
Переберем все варианты выпадения:
Всего 8 возможных исходов, из которых только 1 благоприятный. Т.о. искомая вероятность равна: 1/8=0,125.
Решение: Эту задачу так же можно решить двумя способами.
1/36+1/36+1/36+1/36+1/36=5/36≈ 0,14. (применили сложения вероятностей).
2 способ. Найдем число возможных исходов, переберём все варианты бросков. В подобных задачах удобнее составлять таблицу. Составим таблицу для суммы двух костей. ( все варианты суммы, которые могут выпасть):
Всего исходов 36 (6 на 6). Благоприятных исходов 5 ( легко подсчитать в таблице). Вероятность того, что в сумме выпадет 8 очков, равна: 5/36≈0, 14.
№ 24. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение: 1способ. Найдем число возможных исходов, перебрав все варианты бросков. Составим таблицу, т.к. при решении подобных задач это удобно.
Всего возможных исходов 4. Орел выпадет один раз во втором и третьем вариантах. То есть число благоприятных исходов 2. Вероятность того, что орел выпадет ровно один раз равна: 2/4=0,5.
Найдем все комбинации при двух бросках, когда орел выпадает ровно один раз:
Вероятность выпадения орла (впрочем, как и решки) при одном броске равна 0, 5.
Найдем вероятность выпадения первой комбинации: орел и решка. Решка при втором броске должна выпасть при условии выпадения орла при первом броске, значит, применяем теорему о произведении :0,5*0,5=0,25.
Вероятность выпадения второй комбинации находим так же:0,5*0,5=0,25.
Вероятность появления одной из этих комбинаций находим, как сумму вероятностей:
№ 25. Перед началом матча по футболу судья бросает монету, что бы определить, какая из команд будет первая владеть мячом. Команда «Белые» по очереди играет с командами «Красные», «Синие», и «Зеленые». Найдите вероятность того, что ровно в одном матче право первой владеть мячом получит команда «Белые».
Решение: Пусть разыгрывается первенство владения мячом между командами «Белые» и «Красные». При бросании монеты вероятность того, что право владеть мячом первой у команды «Белые» равна 0,5. Вероятность, что у неё не будет этого права тоже равна 0,5. Такие же вероятности будут и при разыгрывании первенства владения мячом по отношению команд «Синие» и «Зеленые».
Для того, что бы ровно в одном матче право первой владеть мячом получила команда «Белые» рассмотрим все возможные расклады:
Других раскладов, учитывая условие задачи, быть не может.
Т.к. каждый из этих раскладов независимые события, из которых должно произойти одно,
то искомую вероятность находим как сумму: 0,125+0,125+0,125 = 0,375.
№ 26. Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера Б с вероятностью 0,6. Если А играет чёрными, то А выигрывает у Б с вероятностью 0,4. Гроссмейстеры А и Б играют две партии, причем АО второй партии меняют цвет фигур. Найдите вероятность того, что А выиграет оба раза.
Решение: Один раз гроссмейстер А будет играть белыми и вероятность его выигрыша в этом случае согласно условию равна 0,6. Второй раз гроссмейстер А будет играть обязательно черными (т.к. цвет фигур меняется) и вероятность его выигрыша равна в этом случае 0,4. Поскольку эти два события совместны, то их вероятности перемножаем: 0,6*0,4=0,24.
№ 27. В некоторой местности наблюдении показали:
Если июньское утро ясное, то вероятность дождя в этот день 0,1.
Если июньское утро пасмурное, то вероятность дождя в течение дня равна 0,4.
Вероятность того, что утро в июне будет пасмурным, равна 0,3.
Найдите вероятность того, что в случайно взятый июньский день дождя не будет.
Решение: Возьмем случайно взятый июньский день. Утро в этот день может быть пасмурным( вероятность 0,3) или ясным (вероятность 1-0,3=0,7). Если утро пасмурное, то вероятность того, что дождя не будет равна 1-0,4=0,6. Найдем вероятность того, что в при пасмурном утре пойдет дождь: 0,3*0,6=0,18 (вероятности перемножаются, потому что эти события совместные).
Если утро ясное, то вероятность, что дождя не будет равна 1-0,1=0,9. Найдем вероятность того, что при ясном утре пойдет дождь: 0,7*0,9=0,63 (вероятности перемножаются, потому что эти события совместные). Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: 0,18+0,63=0,81.
№ 28. Две фабрики выпускают одинаковые стёкла для автомобильных фар.
Решение: 0,3*0,03=0,009 0,7*0,04=0,028 0,028+0,009=0,037. В ответе ответ:0,043.
Типовые тестовые задания «Математика. ЕГЭ» 2013 г. под ред. А.Л. Семенова, И.В. Ященко. Изд-во «Экзамен» Москва 2013.
«ЕГЭ. 2013. Математика» Авторы-составители: И.Р.Высоцкий, Д.Д. Гущин. АСТ. Астрель. Москва