Найти среднюю скорость поезда если известно что на прохождение отдельных участков дистанции
Скорость. Единицы скорости. Расчет пути и времени движения
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
110. Выразите в метрах в секунду (м/с) скорости: 60 км/ч; 90 км/ч; 300 км/ч; 120 м /мин.
111. Пассажирский самолет летит со скоростью 414 км/ч. Выразите эту скорость в м/с.
414 км/ч = 414000 м/ч = 115 м/с
112. Скорость мотоцикла 20 м/с, а скорость гоночного автомобиля – 360 км/ч. Чья скорость больше и во сколько раз?
113. Автомобиль прошел расстояние 500 м за 25 с. Найти скорость автомобиля.
114. Танк Кристи (рис. 12) развивает скорость при движении на колесах 100 км/ч, а при движении на гусеницах 60 км/ч. Определите, за какое время этот танк пройдет расстояние в 450 км?
115. Пуля, выпущенная из винтовки, долетела до цели, находящейся на расстоянии 1 км, за 2,5 секунды. Найти скорость пули.
116. Самолет развивает скорость 180 км/ч. Какое расстояние может пролететь этот самолет за 25 минут?
117. Два автомобиля движутся равномерно. Первый в течение 5 мин проходит 6 км, а второй в течение 3 с – 90 м. Скорость какого автомобиля больше?
118. Пароход, двигаясь против течения со скоростью 14 км/ч, проходит расстояние между двумя пристанями за 4 часа. За какое время он пройдет то же расстояние по течению, если его скорость в этом случае равна 5,6 м/с?
119. В подрывной технике для взрыва шпуров (скважин, наполненных взрывчатым веществом) применяют особый, сгорающий с небольшой скоростью шнур (бикфордов шнур). Какой длины шнур надо взять, чтобы успеть, после того как он зажжен, отбежать на расстояние 150 м, если скорость бега 5 м/с, а скорость распространения пламени по шнуру 0,8 м/с?
120. Земноводный танк может двигаться на гусеницах по суше со скоростью 70 км/ч и плавать со скоростью 10 км/ч. Сколько времени потребуется этому танку, чтобы пройти общее расстояние 61 км, если на пути буде озеро шириною в 5 км?
121. Двигаясь равномерно, пассажирский реактивный самолет ТУ-104 пролетел 8250 м за 30 с. Какова скорость самолета в м/с и км/ч?
122. Пешеход прошел 900 м за 10 мин. Вычислите его среднюю скорость движения (в м/с).
123. При испытании скорости револьверной пули при вылете оказалось, что расстояние между двумя картонными пластинками длиною в 20 см пуля пролетела за 0,0004 секунды. Определить по этим данным скорость пули.
124. Скоростной лифт в небоскребе поднимается равномерно со скоростью 3 м/с. За сколько времени можно подняться на таком лифте на высоту 90 м?
125. Длина конвейера 20 м. За какое время вещь, поставленная у начала конвейера, придет к его концу, если скорость движения конвейера 10 см/с?
126. Клеть подъемной машины в шахте опускается со скоростью 4 м/с. За какое время можно достигнуть дна глубины шахты глубиной 300 м?
127. Автомобиль проехал равномерно участок дороги длиной 3,5 км за 3 мин. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак «скорость не более 50 км/ч» (рис. 13)?
128. Какой путь пролетит реактивный истребитель, двигающийся со скоростью 3600 км/ч, за 5 ч?
129. Велосипедист едет со скоростью 5 м/с. За какое время он преодолеет 99 км?
130. Скорость автомобиля 180 км/ч, а скорость самолета 600 м/с. Сколько времени затратят автомобиль и самолет для прохождения пути в 2000 м?
132. Длина земного экватора 40000 км. За какое время самолет может облететь Землю по экватору, если его скорость равна 800 км/ч?
133. В морском деле принимается за единицу скорости узел. Вычислите, скольким км/ч соответствует 1 узел, если известно, что 1 узел = 1 морская миля/ч и 1 морская миля равна длине дуги земного экватора, соответствующей одной минуте градусного измерения (длина дуги экватора равна 39805 км).
134. Росток бамбука за сутки вырастает на 86,4 см. На сколько он вырастает за 1 мин?
135. Спортсмен пробегает дистанцию в 60 м за 9,4 с. С какой скоростью он бежит?
136. В течение двух часов поезд двигался со скоростью 110 км/ч, затем сделал остановку на 10 мин. Оставшуюся часть пути он шел со скоростью 90 км/ч. Какова средняя скорость поезда на всем пути, если он прошел 400 км?
137. Автобус за первые два часа проехал 90 км, а следующие три часа двигался со скоростью 50 км/ч. Какова средняя скорость автобуса на всем пути?
138. Мотоциклист едет первую половину пути со скоростью 90 км/ч, а вторую половину пути – со скоростью 70 км/ч. Найдите среднюю скорость мотоцикла на всем пути.
139. Средняя скорость велосипедиста на всем пути равна 40 км/ч. Первую половину пути он ехал со скоростью 60 км/ч. С какой скоростью велосипедист проехал остаток пути?
140. Изобразите графически векторы скорости: 5 км/ч; 15 км/ч; 10 м/с.
141. Приняв, что сторона одной клеточки в тетради равна скорости 1 м/с, изобразите в тетради скорость 5 м/с.
142. На графике скорость 3,6 км/ч изображена стрелкой длиной 2 см. Изобразите в том же масштабе скорость 2 м/с.
143. По графику зависимости пути от времени на рисунке 14 определите скорость при равномерном движении (в м/с).
144. На рисунке 15 изображен график движения лыжника. Сколько метров он проедет за 12 мин, если его скорость останется неизменной?
145. Гоночный автомобиль мчится со скоростью 360 км/ч. Начертите в тетради график зависимости его пути от времени.
146. Аэроплан летит со скоростью 720 км/ч в течение 25 мин. Начертите график его движения, приняв для оси времени масштаб: 5 мин – 1 см; а для оси пути масштаб выберите самостоятельно.
147. Расстояние между двумя пристанями 144 км. Сколько времени потребуется пароходу для совершения рейса между пристанями туда и обратно, если скорость парохода в стоячей воде 18 км/ч, а скорость течения 3 м/с?
148. Самолет, летящий со скоростью 300 км/ч, пролетел расстояние между аэродромами А и В за 2,2 ч. Обратный полет из-за встречного ветра он совершил за 2,4 ч. Определите скорость ветра.
149. С двух пристаней, расстояние между которыми 70 км, одновременно отправляются два парохода навстречу друг другу. Пароходы встретились через 2,5 ч, причем пароход, идущий по течению, прошел за это время путь 55,5 км. Скорость течения 2 м/с. Определите скорости пароходов в стоячей воде.
150. Определите по графику пути равномерного движения, изображенному на рисунке 16:
а) путь, пройденный телом в течение 4,5 с,
б) время, в течение которого пройден путь 15 м,
в) скорость движения,
если сторона клетки соответствует 1 м и 1 с.
а) 18 м; б) 3,75 с; в) 4 м/с
151. Постройте на одном и том же чертеже графики путей двух равномерных движений со скоростью 7,2 км/ч и 18 км/ч.
152. Постройте график пути движения, уравнение которого s = 5t.
153. На рисунке 17 дан график пути движения поезда. Определите, в котором часу отправился поезд и направление его движения.
В 7 часу, в направлении Москва → Серпухов
154. На рисунке 18 дан график пути движения поезда. Определите скорости движения на участках, изображенных отрезками графика ОА, АВ и ВС. Какой путь пройден поездом в течение 3 часов с начала его движения?
155. Постройте график пути движения поезда между станциями А и В по следующим данным. Расстояние от А до В равно 60 км. Двигаясь от А к В со скоростью 40 км/ч, поезд на полпути делает пятиминутную остановку, потом продолжает двигаться дальше со скоростью 60 км/ч. На станции В поезд стоит 20 мин, затем движется обратно без остановок со скоростью 45 км/ч.
156. От одной и той же станции в одном и том же направлении отправляются два поезда. Скорость первого 30 км/ч, второго 40 км/ч. Второй поезд отправляется через 10 мин после первого. После сорокаминутного движения первый поезд делает пятиминутную остановку, потом продолжает двигаться дальше с прежней скоростью. Определите графически, когда и на каком расстоянии от станции второй поезд догонит первый. Графическое решение проверьте вычислением.
157. Чем отличаются движения I и II, графики которых даны на рисунках 19 и 20? Что обозначает точка пересечения графиков и что по ней можно узнать?
158. По графику движения корабля, подходящего к причалу (рис. 21), определите скорость его движения на участке АВ.
159. По представленному на рисунке 21 графику движения корабля, подходящего к причалу, дайте характеристику движения корабля на участках АВ, ВС и CD.
АВ – равномерное
ВС – равнозамедленное
CD – движение отсутствует
160. По графику на рисунке 21 определите среднюю скорость движения корабля за промежуток времени между 104-й и 106-й минутами движения.
161. На рисунке 22 даны графики движения мопеда (а) и велосипеда (b). Определите скорости их движения. Кто из них поехал раньше?
162. Какую скорость имеют в виду, говоря о скорости движения поезда, автомобиля или самолета между двумя какими-нибудь пунктами?
163. Пуля вылетела из ствола со скоростью 600 м/с.Какую скорость здесь имеют в виду?
164. Поезд прошел 25 км за 35 мин, причем первые 10 км он прошел в течение 18 мин, вторые 10 км в течение 12 мин, а последние 5 км за 5 мин. Определите среднюю скорость поезда на каждом участке и на всем пути.
165. Санки, двигаясь вниз по горе, прошли в течение первой секунды движения 2 м, второй секунды – 6 м, третьей секунды – 10 м и четвертой секунды – 14 м. Найдите среднюю скорость за первые две секунды, за последние две секунды и за все время.
166. Почему нельзя говорить о средней скорости переменного движения вообще, а можно говорить только о средней скорости за данный промежуток времени или о средней скорости на данном участке пути?
Потому что тело всегда проходит определенный путь за определенное время.
167. Постройте на одном чертеже графики скоростей двух равномерных движений: v1 = 3 м/с и v2 = 5 м/с. Построить на том же чертеже прямоугольники, площади которых численно равны путям, пройденным в течение 6 с.
168. Даны графики зависимости пройденного пути от времени при равномерном движении, представленные в одном масштабе. Как по ним определить, какое тело движется с большей скоростью?
Чем больше угол между графиком и осью времени, тем выше скорость.
Чем меньше угол между графиком и осью расстояния, тем выше скорость.
Как найти среднюю скорость
Как же рассчитать скорость
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
Можно записать использовать и такой вид вычислений:
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Упражнения
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.
Какую скорость переменного движения показывает спидометр автомобиля?
Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.
В каком случае мгновенная и средняя скорости равны между собой? Почему?
При равномерном движении. Потому что скорость не изменяется.
Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?
Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?
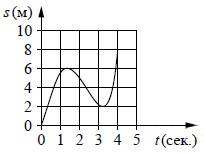
*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.
Задача решается графическим способом. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики движения шариков приведены на рисунке. Так как пути. пройденные шариками, равны, то, как видно из графика (на графике пути численно равны площадям заштрихованных фигур), время второго шарика меньше времени первого.
Не упустите
Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:
Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.
Вот так легко запоминается формула «скорость, время, расстояние»
Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено
Для чего это нужно
Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.

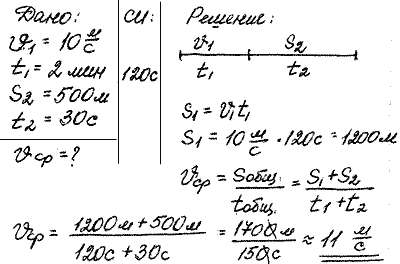
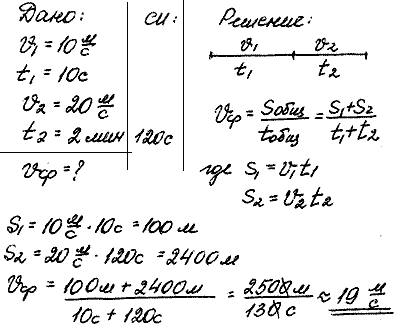
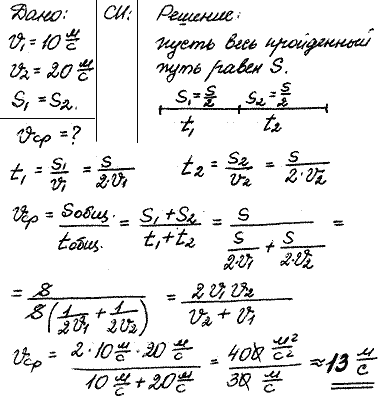



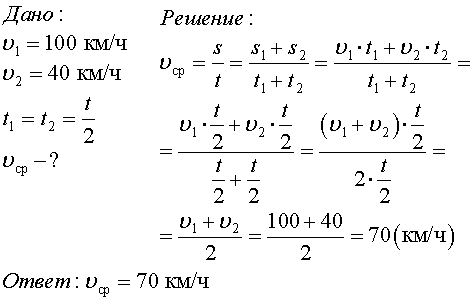
Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.
Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.
Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.
Часто водителю необходимо отыскать такой важный показатель, как средняя скорость автомобиля после той или иной поездки. Иногда эта цифра будет важным фактом для водителя транспорта компании, а в иных случаях — просто интересное число для владельца транспортного средства. В любом случае, расчет средней скорости важен для многих водителей. В современных автомобилях, оснащенных эффективными компьютерными системами управления, достаточно просто выбрать нужный режим отображения информации на экране компьютера, чтобы узнать среднюю скорость за определенный промежуток времени или пробег.
Для вычисления средней скорости поездки на современной машине достаточно подготовиться заранее, сбросив показатели суточного пробега на нуль, а также обнулив средние данные расхода и скорости. После этого вы сможете не засекать никакого времени, а также не продумывать формулы по расчету средней скорости поездки. Тем не менее, такой вариант не всегда подходит, да и не все автомобили оснащены хорошим бортовым компьютером. Потому следует разобраться с тем, как определять среднюю скорость и прочие параметры.
Постоянная скорость
Самый простой случай в физике — равномерное движение. Скорость постоянна, не меняется на протяжении всего пути. Есть даже скоростные константы, сведенные в таблицы, — неизменные величины. К примеру, звук распространяется в воздухе со скоростью 340,3 м/с.
А свет — абсолютный чемпион в этом плане, он обладает самой большой в нашей Вселенной скоростью — 300 000 км/с. Эти величины не меняются от начальной точки движения до конечной. Они зависят только от среды, в которой движутся (воздух, вакуум, вода и пр.).
Равномерное движение часто встречается нам и в повседневной жизни. Так работает конвейер на заводе или фабрике, фуникулер на горных трассах, лифт (за исключением очень коротких периодов пуска и остановки).
График такого движения очень прост и представляет собой прямую линию. 1 секунда — 1 м, 2 секунды — 2 м, 100 секунд — 100 м. Все точки находятся на одной прямой.
Частные случаи нахождения средней скорости
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
| Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения. |
Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Находим среднюю скорость и средний расход поездки по факту
Если замеры средней скорости поездки важны для вас в коммерческих целях или в качестве отчетности для фирмы, в которой вы работаете, то проще всего купить GPS-навигатор, который обладает функцией учета скорости и времени, проведенного в дороге. Этот прибор полностью заменит бортовой компьютер и сможет без применения различных формул показать вам среднюю скорость поездки.
В иных случаях можно пользоваться более грубыми методами определения. Для замеров вам потребуется секундомер, который будет определять рабочее время поездки. То есть, для нас важна каждая секунда, которую автомобиль проводит в дороге. Время, проведенное на заправках или в придорожных кафе зачастую в расчет не входит. Задачи для точного замера следующие:
Предположим, на поездку у вас ушло ровно 5 часов, а пройденное по спидометру расстояние оказалось 300 километров. Это значит, что средняя скорость вашего автомобиля во время движения составила 60 км/ч. Если вы будете практиковать определение средней скорости для каждой дальней поездки, то будете удивлены низкими показателями.
Часто создается впечатление, что средняя скорость должна быть около 120 километров в час, но на деле оказывается меньше 60. Подобным образом вы сможете просчитать средний расход топлива. Нужно затраченные литры поделить на сотни километров пройденного расстояния. К примеру, если вы проехали 300 километров, то делать сумму литров нужно на 3.
Аналог средней температуры в механике
В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о «частях» пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, «первую половину пути поезд следовал со скоростью…», или «первую треть пути пешеход прошагал соскоростью…», и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S 1 = S 2 = … = S n и точные значения скоростей v 1, v 2, … v n, наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения v складываются и делятся на n. В итоге ответ получается неверный.
Уровень B
1. О какой скорости – средней или мгновенной – идет речь в следующих случаях:
а) пуля вылетает из винтовки со скоростью 800 м/с;
б) скорость движения Земли вокруг Солнца 30 км/с;
в) на участке дороги установлен ограничитель максимальной скорости – 60 км/ч;
г) мимо вас проехал автомобиль со скоростью 72 км/ч;
д) автобус преодолел расстояние между Могилевом и Минском со скоростью 50 км/ч?
2. Путь в 63 км от одной станции до другой электропоезд проходит за 1 ч 10 мин со средней скоростью 70 км/ч. Какое время занимают остановки?

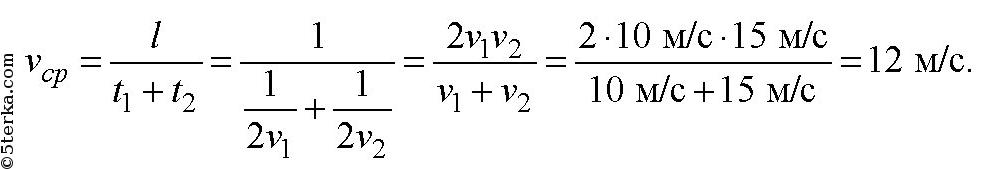


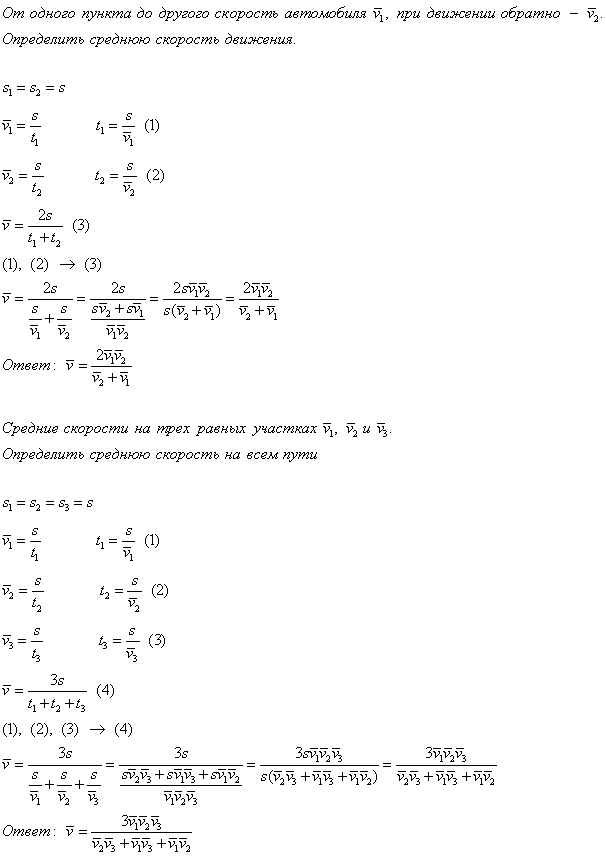




3. Самоходная косилка имеет ширину захвата 10 м. Определите площадь поля, скошенного за 10 мин, если средняя скорость косилки 0,1 м/с.
4. На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение 10 мин, а затем проехал подъем со скоростью 36 км/ч за 20 мин. Чему равна средняя скорость на всем пути?
5. Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 12 км/ч, а вторую половину времени (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость движения велосипедиста.
6. Школьник проехал 1/3 всего времени на автобусе со скоростью 60 км/ч, еще 1/3 всего времени на велосипеде со скоростью 20 км/ч, остальное время прошел со скоростью 7 км/ч. Определите среднюю скорость движения школьника.
7. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч, а вторую половину (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость его движения.
8. Из одного пункта в другой мотоциклист двигался со скоростью 60 км/ч, обратный путь им был пройден со скоростью 10 м/с. Определите среднюю скорость мотоциклиста за все время движения.
9. Школьник проехал 1/3 пути на автобусе со скоростью 40 км/ч, еще 1/3 пути на велосипеде со скоростью 20 км/ч, последнюю треть пути прошел со скоростью 10 км/ч. Определите среднюю скорость движения школьника.
10. Пешеход часть пути прошел со скоростью 3 км/ч, затратив на это 2/3 времени своего движения. Оставшееся время он прошел со скоростью 6 км/ч. Определите среднюю скорость.
11. Скорость поезда на подъеме 30 км/ч, а на спуске – 90 км/ч. Определите среднюю скорость на вcем участке пути, если спуск в два раза длиннее подъема.
12. Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч?
Средняя скорость — машина
Средняя скорость машин ЕС-1030 по Гибсону составляет 100 тыс. операций в секунду.
Под средней скоростью машины понимают среднюю линейную скорость одной из точек ведущего вала машины во время ее установившегося движения.
Для того чтобы средняя скорость машины могла оставаться постоянной, необходимо, чтобы при этой скорости имело место равновесие между работой движущих сил и работой сопротивлений. Но это равновесие может нарушаться по различным причинам.
Для установления козфициента нагрузки двигателя определим среднюю скорость машины v — кгк, момент трения по формуле ( 55), угловую скорость машины ( см. фиг.
Очевидно, что такая система позволяет на уровне программирования заботиться о том, чтобы информация была заранее считана в быстрые регистры операндов и арифметическое устройство не ожидало ее поступления из памяти. Средняя скорость машины CDC-6600 оценивается в 3 5 млн. операций в секунду, однако, как утверждают разработчики, при оптимальном программировании она может быть значительно повышена.
Сравнение формул ( 52) и ( 58) дает следующий вывод: коэфициент нагрузки двигателя на повороте при бортовых фрикционах в два раза меньше, чем при простом дифе-ренциале. Это снижение нагрузки достигается за счет снижения потери в тормозе, а также вследствие понижения средней скорости машины на повороте. Зависимость между коэ-фициентами нагрузки двигателя и параметром поворота показана на диаграмме фиг.
Если бы движение машины было равномерно, если бы она шла всегда одинаково быстро, то оценка 40 км в час полностью характеризовала бы ее скорость — одну и ту же в любой момент движения. Но машина движется неравномерно; за час скорость ее много раз резко меняется, и когда нам говорят, что машина прошла в час 40 км, то это дает нам представление лишь о некоторой средней скорости машины за этот час и ничего не говорит о скорости ее в тот или другой определенный момент, в том или другом определенном месте ее пути. Час — это слишком большой промежуток времени, за который скорость движения машины может меняться много раз.
Средняя скорость машины при выполнении арифметики тем самым приблизительно равна 10000 операций в секунду. При выполнении логических программ быстродействие резко возрастает. В минимальном комплекте в состав процессора входит оперативная память объемом 8192 байта. Правда, объем памяти при необходимости может быть расширен до 64 Кбайт.
На маршруте ABCDE длиной 147 км Турист может сам выбирать способ передвижения. На обратном пути из пункта Е в пункт А он поступил по-другому: до пункта D дошел пешком, преодолев расстояние в 24 км, в пункте D пересел на лошадь и добрался до пункта В за 3 ч 20 мин, а от пункта Л до пункта А доехал на машине за 1 ч 12 мин. Определите скорость передвижения туриста на машине и на лошади, если средние скорости машины и лошади были постоянными при движении от А к S и обратно.
Частные случаи нахождения средней скорости
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
| Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения. |
Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Главная >  Wiki-учебник >  Физика > 7 класс >
Формула скорости математика 4 класс
С какой скоростью черепах ползла после камня, если она проползла 33 см?
3. Поезд шёл до станции 7 ч со скоростью 63 км/ч, а после станции поезд проехал ещё 4 ч. С какой скоростью поезд проедет путь от станции, если всего он прошёл 741 км?








Составные задачи на расстояние.
Травоядный динозавр сначала бежал 3 ч со скоростью 6 км/ч, а потом он бежал ещё 4 ч со скоростью 5 км/ч. Какое расстояние пробежал травоядный динозавр?
Рассуждаем так. Это задача в одном направлении.
Слова « скорость », «время», «расстояние» запишем зеленой ручкой.
Скорость (V) Время (t) Расстояние (S)
Составим план решения этой задачи. Чтобы узнать какое расстояние пробежал динозавр, надо знать, какое расстояние он пробежал, потом и какое расстояние он пробежал сначала.
Чтобы найти расстояние, надо скорость умножить на время.
6· 3 = 18 (км) — расстояние, которое пробежал динозавр сначала. Чтобы найти расстояние, надо скорость умножить на время.
5 4 = 20 (км) — расстояние, которое пробежал динозавр потом.
Составим выражение:6 3 + 5 4 = 38(км)
Ответ: 38 км пробежал травоядный динозавр.
1. Ракета сначала летела 28 с со скоростью 15 км/с, а оставшийся путь летела 53 с со скоростью 16 км/с. Какое расстояние пролетела ракета?
2. Утка сначала плыла 3 ч со, скоростью 19 км/ч, а потом она плыла ещё 2 ч со скоростью 17 км/ч. Какое расстояние проплыла утка?
3. Кит полосатик сначала плыл 2 ч со скоростью 22 км/ч, а потом он плыл ещё 2 ч со скоростью 43 км/ч. Какое расстояние проплыл кит полосатик?
4. Теплоход до пристани шёл 3 ч со скоростью 28 км/ч, а после пристани плыл ещё 2 ч со скоростью 32 км/ч. Какое расстояние проплыл теплоход?
Задачи на нахождение времени совместной работы.
Привезли 240 саженцев елей. Первый лесник может посадить эти ели за 4 дня, а второй за 12 дней. За сколько дней оба лесника могут выполнить задание, работая вместе?
240: 4 = 60 (саж,) за 1 день сажает первый лесник.
240: 12 — 20 (саж.) за 1 день сажает второй лесник.


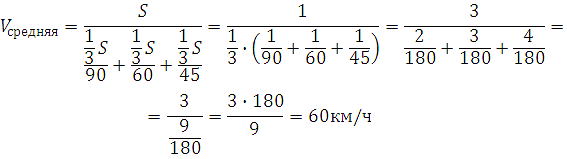


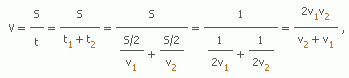
60 + 20 = 80 (саж.) за 1 день сажают оба лесника. 240:80 = 3(дн.)
Ответ: за 3 дня лесники посадят саженцы, работая вместе.
1. В мастерской 140 мониторов. Один мастер отремонтирует их за 70 дней, а другой, за 28 дней. За сколько дней оба мастера отремонтируют эти мониторы, если будут работать вместе?
2. Было 600 кг горючего. Один трактор израсходовал его за 6 дней, а другой – за 3 дня. За сколько дней тракторы израсходуют это горючее, работая вместе?
3. Надо перевезти 150 пассажиров. Один катер перевезёт их за 15 рейсов, а другой за 10 рейсов. За сколько рейсов эти катера перевезу всех пассажиров, работая вместе?
4. Один ученик может сделать 120 снежинок 60 мин, а другой — за 30 мин. Сколько потребуется времени ученикам, если они будут работать вместе?
5. Один мастер может изготовить 90 шайбочек за 30 мин, другой—‘за 15 мин. За какое время они изготовят 90 шайбочек при совместной работе?
Основные понятия и законы кинематики
кинематикойМеханическим движениемСистемой отсчётаТелом отсчётаМатериальной точкойТраекториейпрямолинейноекриволинейное
Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось)
А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещенияСкоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
Ускорением
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x + Vxt, где x — начальная координата тела, Vx — скорость движения.Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением 
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:
Средняя скорость — движение — автомобиль
Средняя скорость движения автомобиля зависит от максимальной скорости, которую он может развить на дорогах различного качества, и от интенсивности разгона. Кроме того, на среднюю скорость автомобиля существенное влияние оказывают его тормозные свойства.
Средние скорости движения автомобилей приведены для дорог с усовершенствованным типом покрытия в хорошем состоянии.
Средняя скорость движения автомобиля составляет v км / час.
Средняя скорость движения автомобиля зависит от многих факторов: на нее влияют, с одной стороны, конструктивные особенности автомобиля, а с другой — дорожные условия. При испытаниях ее стремятся поддерживать максимально возможной. Чтобы полнее выяснить причины, вызывающие ограничение скорости, принято определять среднюю скорость чистого движения и среднюю техническую скорость.
Стремление повысить среднюю скорость движения автомобилей ( автопоездов) при одновременном увеличении их полной массы приводит к повышению мощности двигателя, что, в свою очередь, вызывает повышенные требования к трансмиссии автомобиля. Это непосредственно относится и к ведущему мосту, назначение которого состоит в изменении крутящего момента двигателя при передаче его к ведущим колесам таким образом, чтобы вместе с коробкой передач обеспечить согласование скоростной характеристики двигателя с динамической характеристикой автомобиля.
| График, для определения нагрузочного режима трансмиссии автомобиля ( по нормали. |
Угловую скорость рассчитываемых подшипников определяют по средней скорости движения автомобиля аа ср — с учетом соответствующего передаточного числа между валами коробки передач.
Именно эта скорость имеется в виду, когда, например, говорят о средней скорости движения автомобиля или средней скорости поезда.
За эквивалентное число оборотов пэкв принимается число оборотов подшипника ( вала), соответствующее средней скорости движения автомобиля на основной ( прямой) передаче.
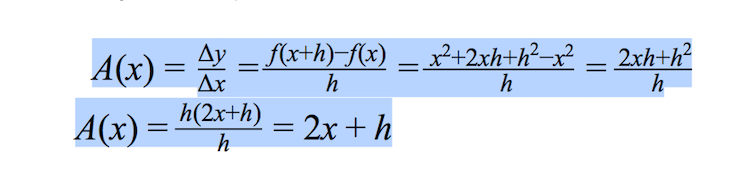





| Зависимость коэффициента сцепления от различных факторов. |
В практике управления автомобилем важно знать н только максимальную скорость движения автомобиля на отдельных участках маршрута, но и среднюю скорость на всем маршруте. Возможность определения средней скорости движения автомобиля имеет практическое значение для осуществления планирования перевозок грузов и пассажиров на автомобильном транспорте.
Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости
В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.



































































