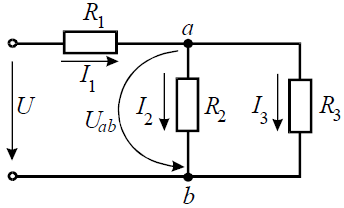
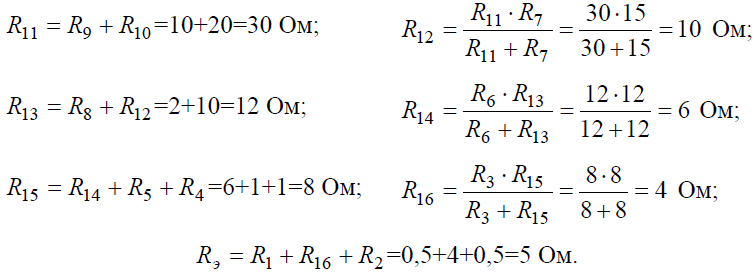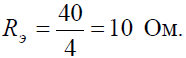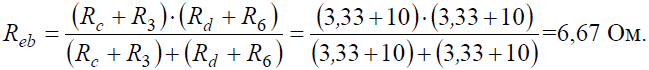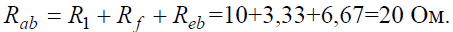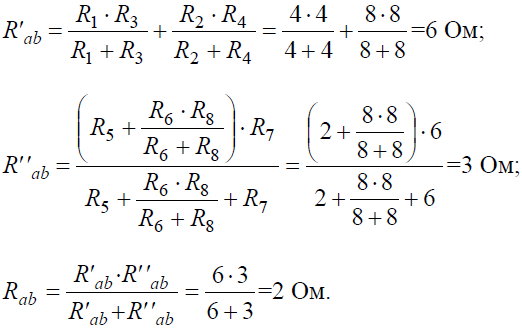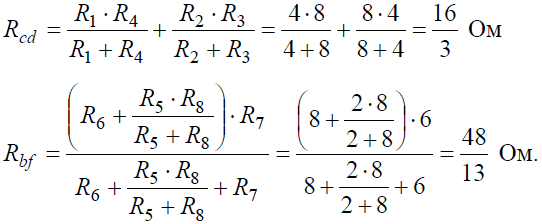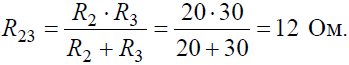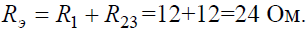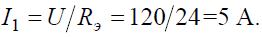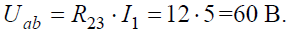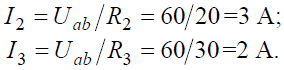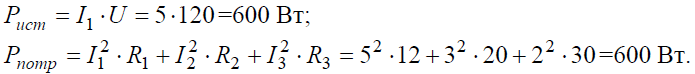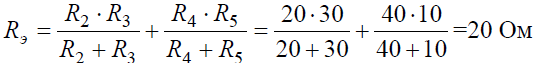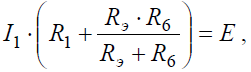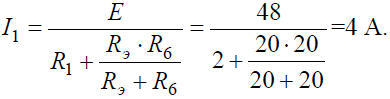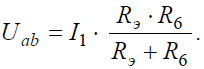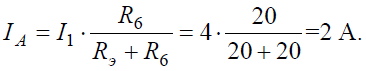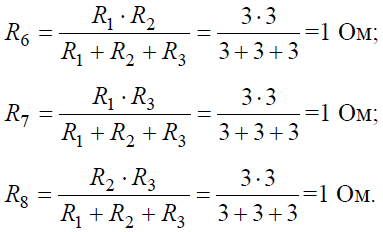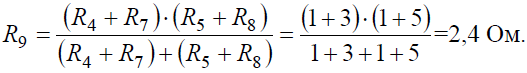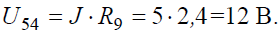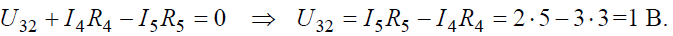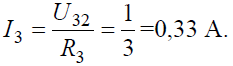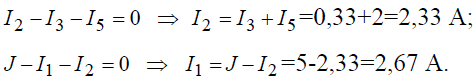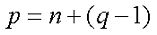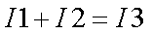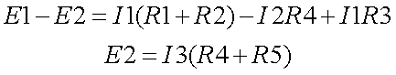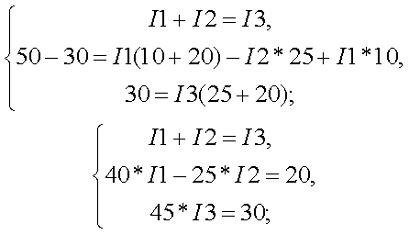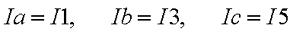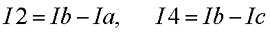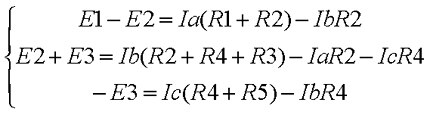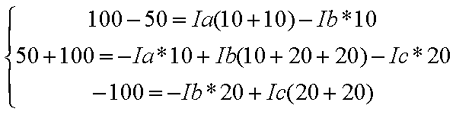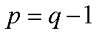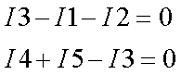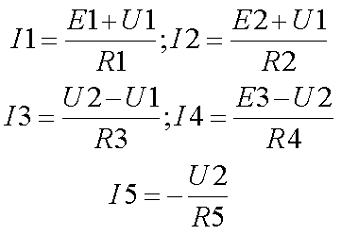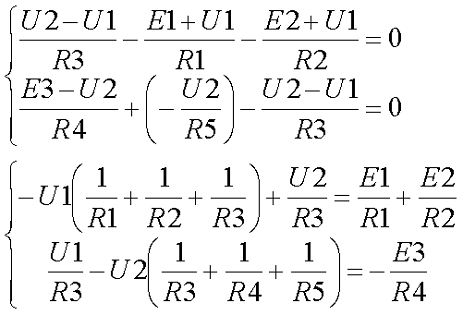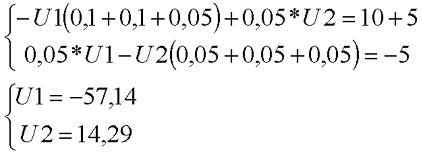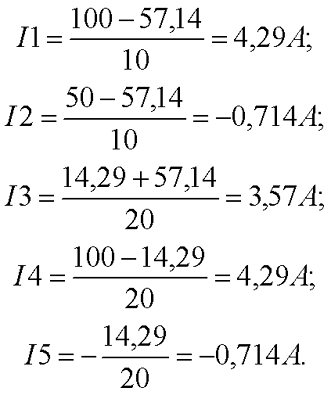Найти токи i1 i2 i3 если известно что u 35 в

Общая схема делителя тока представлена на рис.1.

Рис.1 – Общая схема делителя тока

Выведем общую формулу, позволяющую найти любой из этих токов.

Для нахождения тока I заменим все резисторы эквивалентным (рис.2).

Рис.2 – Схема замещения резисторов

Сопротивление эквивалентного резистора найдем из формулы параллельного соединения сопротивлений:

(1)

К сопротивлению Rэкв приложено напряжение U, значит, через этот резистор потечет ток I, который можно найти по закону Ома:

(2)

Значение тока I и сопротивление Rэкв нам известно, выразим U из формулы (2) и подставим

Rэкв из выражения (1):

(3)

Выведем общую формулу, по которой можно найти ток в любой ветке.

Найдем значение тока в i-й ветке по закону Ома:

(4)

Сопротивление резистора Ri (резистор в i-й ветке) нам известно, подставим в формулу (4) U

5)

То есть, по формуле

(6)

можно найти ток в любой ветке.

В случае с двумя сопротивлениями (n=2) формула существенно упрощается.

Схема делителя тока с двумя резисторами показана на рис.3.

Рис.3 – Схема делителя тока с двумя резисторами

Формула (6) преобразуется:

(6)

По этой формуле найдем токи I1, I2:

(7)

(8)

Источник

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда » в эквивалентный «треугольник » и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.

Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

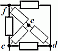
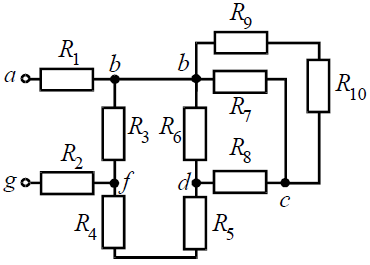
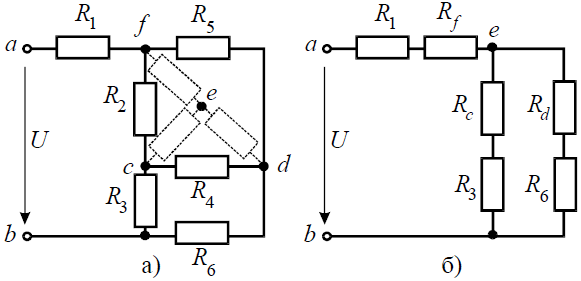
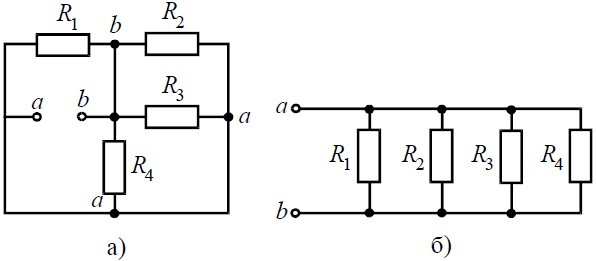
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

Рис. 2

где R – величина сопротивления, Ом;

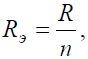
n – количество параллельно соединенных сопротивлений.

По условию задачи величины всех сопротивлений равны, а значит:

На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:

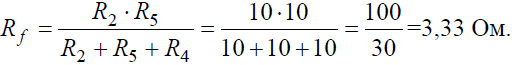
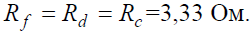
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:

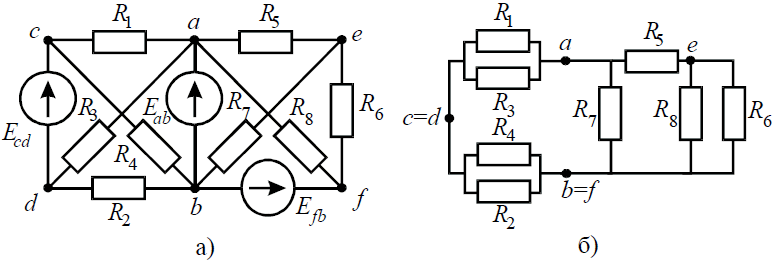
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей R_cd и R_bf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает ») из схемы сопротивления R₁, R₂, R₃, R₄ в первом случае, и R₅, R₆, R₇, R₈ во втором случае.

Эквивалентное сопротивлениедля параллельно включенных сопротивлений:

Эквивалентное сопротивление всей цепи:

Ток в неразветвленной части схемы:

Напряжение на параллельных сопротивлениях:

Токи в параллельных ветвях:

Баланс мощностей:

Величина эквивалентного сопротивления:

Напряжение на зажимах параллельных ветвей U_ab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием R_Э и R₆:

Тогда амперметр покажет ток:

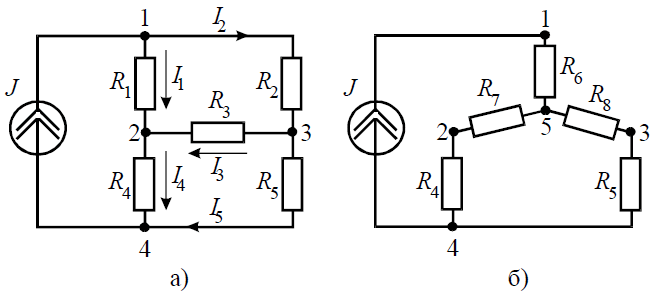
Преобразуем параллельное соединение ветвей между узлами 4 и 5

Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:

Возвращаясь к исходной схеме, определим напряжение U₃₂ из уравнения по второму закону Кирхгофа:

Тогда ток в ветви с сопротивлением R₃ определится:

Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:

Метод эквивалентных преобразований

Источник

ElectronicsBlog

Обучающие статьи по электронике

Электротехника Часть 5 Методы расчёта электрических цепей

Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Расчёт электрических цепей с помощью законов Кирхгофа

Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.

Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров. Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур. Таким образом, количество уравнений в системе уравнений по данному методу расчёта цепи будет определяться следующим выражением

В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже

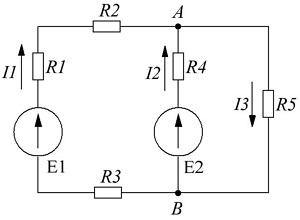
Пример электрической цепи для расчёта по законам Ома и Кирхгофа.

В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.

Таким образом, получившаяся система уравнений будет иметь следующий вид

Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.

В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.

Метод контурных токов

Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже

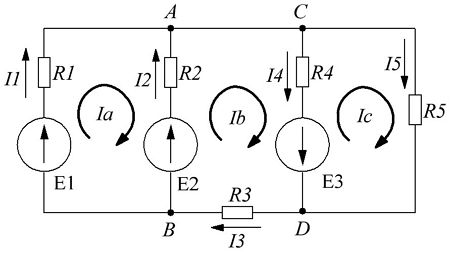
Расчет цепи методом контурных токов.

Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.

В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях

Остальные же токи можно найти как разность двух контурных токов

В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

Метод узловых напряжений

Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает

где q – количество узлов в электрической цепи.

Принцип расчёта электрической цепи заключается в следующем:

В качестве примера возьмём предыдущую цепь и составим систему уравнений

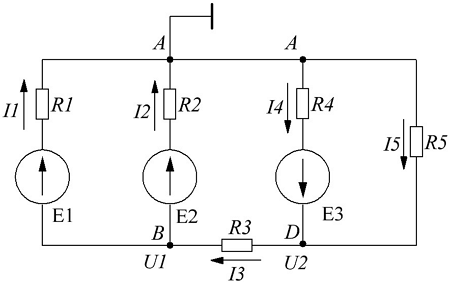
Схема для решения уравнений методом узловых потенциалов.

В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа

Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома

В результате получившаяся система будет иметь следующий вид

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник

Задачи на тему «электротехника»

R =0,05 м Ответ: 2,16 Н

В цепи Е=100В; R ₁ =10 Ом; R ₂ =20 Ом; R ₃ = R ₄ = 40 Ом

Вычислить токи I ₁ ; I ₂ ; I ₃

Определяем общее сопротивление цепи

Вычисляем точки I ₂ и I ₃

Определить значение ЭДС, если R ₁ = 10 Ом, R ₂ = 20 Ом, R ₃ = 30 Ом, R ₄ = 140 Ом, ток I ₁ =1 A

Найдем общее сопротивление цепи: R _общ = R ₁ + R ₄ ; т.к. сопротивление амперметра равно нулю, то R _общ = 10+140=150 (Ом)

Вычисляем значение Е: Е= I ₁ · R _общ = 1·150 = 150 (В)

Дано : E = 100 B

Вычислим сопротивление на участке цепи а б:

Вычислим общее сопротивление цепи:

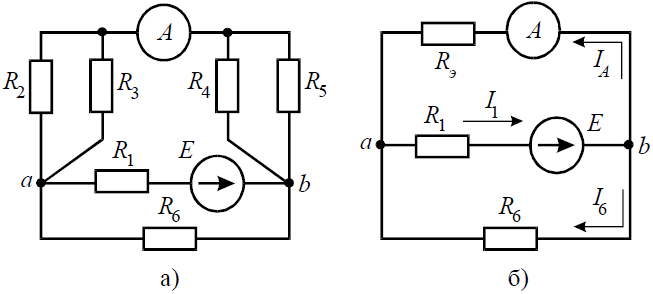
Определить значение Е, если R ₁ =10 Ом; R ₂ =20 Ом; R ₃ =30 Ом; R ₄ =40 Ом; R ₅ =50 Ом; R ₆ =60 Ом

Ток протекающий через R ₄ =1А

Найдем общее сопротивление цепи по постоянному току

По закону Ома: U = I · R _общ

Какова мощность потребления электрической плиты, если потребляемый плиткой ток равен 5 А.

Сопротивление равно 24 Ом

Чему равна сила тока, потребляемая плитой из сети, если сопротивление спирали равно 10 Ом, мощность плиты равна 1000 Вт (Р)

Дано: Р = 1000 Вт; R = 10 Ом Найти: I

P = I 2 · R отсюда = = 10A

Определить индуктивное сопротивление катушки с индуктивностью 0,05 Гц в цепи тока частотой

50 Гц и частотой 400 Гц.

Определить сопротивление конденсатора емкостью 5 Мкф при частоте 50 Гц и при частоте 400 Гц

Дано: U = 220 B ; С ₁ = 20 Мкф, С ₂ = 25 Мкф, С ₃ = 30 Мкф

Решение: Вычислим общую емкость С _общ

Ответ: I = 0,55 А 3) Вычислим ток I =

В сеть 120 В, 50 Гц включена катушка с индуктивностью L = 0,0127 Гн.

Определить ток в цепи

Дано: U = 120 B ; F = 50Гц; L = 0,0127 Гн

Решение: Вычислим реактивное сопротивление катушки

X _L = W _L = 2 π · F · L = 2*3,14*50*0,0127 = 4 (Ом)

В сеть 120 В, 50 Гц включена катушка с индуктивностью 0,0255 Гн и активным сопротивлением 6Ом Определить ток в цепи.

Дано: U = 120 B ; F = 50Гн; L = 0,0255 Гн; R = 6 Ом

Решение: вычислим индуктивное сопротивление

X _L = W _L = 2 π · F · L = 2*3,14*50*0,0255 = 8 (Ом)

Вычислим полное сопротивление цепи

К сети 240 В, 50 Гц присоединена цепь, состоящая из конденсатора емкостью 40 Мкф и сопротивлением 60 Ом. Определить ток I

Дано: U = 240 B ; F = 50Гн; C = 40 Мкф; R = 60 Ом

Решение: Вычислим емкостное сопротивление X _C

Вычислим полное сопротивление цепи

Определить ток цепи.

Решение: определим реактивное сопротивление

X _L = W _L = 2π·F·L = 2*3,14*50*0,382 = 120 ( Ом )

Полное сопротивление цепи

В сеть 120 В, 50 Гц включена катушка с индуктивностью 25,5 мГн и активным сопротивлением 6 Ом

Определить полную мощность цепи.

Решение: Определим активную мощность цепи

Определим реактивную мощность цепи

Полная мощность цепи

S = U · I = 120*12=1440 (ВА) Ответ: S = 1440 BA

Мощность трехфазного асинхронного двигателя равна 2,2 кВт. Определить номинальный ток статора, если cos ƒ = 0,86
Дано: P = 2,2 кВт, U = 380 В, cos ƒ = 0,86
Определить I номинальное статора

Решение: ; отсюда Ответ: I _ном. =3,89 А

Активная мощность трехфазной цепи составляет 20 кВт, а реактивная 15 кВт

Чему равен cos ƒ цепи?

Дано: P = 20 кВт, Q = 15 кВт

Решение: вычислим полную мощность:

Определим коэффициент мощности:

Определить действующее значение тока: I = 282 sin ωt +141 sin 3 ωt +71 sin (5 ωt + ) А

Первичная обмотка трансформатора выполнена в сеть напряжением 10 кВ, на зажимах вторичной обмотки напряжения равно 400 В.

Определить число витков вторичной обмотки, если число витков первичной обмотки равно 21000

Дано: U ₁ = 10000 B ; U ₂ = 400 B ; W ₁ = 21000

Решение: определить коэффициент трансформации

Для определения числа витков вторичной обмотки используем формулу : ; U ₁ W ₂ = U ₂ W ₁

Определить напряжение цепи или сети, которое необходимо приложить к зажимам катушки, что бы создать в ней ток в 5 А, если активное сопротивление катушки R = 6 Ом, а индуктивное сопротивление X _L = 8 Ом

Дано : I = 5A; R = 6 Ом ; X _L = 8 Ом

Решение: определим падение напряжения на сопротивление R

U _R = I * R = 5*6 = 30 B

Индуктивное падение напряжения на катушке

Полное падение напряжения в сети

Определить полное сопротивление цепи, в которой R = 9 Ом, X _L = 120 Ом

В цепи изображенной на схеме, определить показания вольтметра.

Дано : I = 5A; R = 120 Ом ; X _L = 16 Ом

Определить: показания вольтметра Решение:

Вычислим падение напряжения на резисторе R

U _R = I · R = 5*12 = 60 B

Вычисляем падение напряжения на катушке

Показание вольтметра равно

Определим общее сопротивление цепи

U = 5*20 или I * Z = 100 Ом

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Физика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-270484

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В российских школах могут появиться «службы примирения»

Время чтения: 1 минута

Петербургский Политех перевел студентов на дистанционку

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В Хабаровске родители смогут заходить в школы и детсады только по QR-коду

Время чтения: 1 минута

При засыпании человеческий мозг может решать сложные задачи

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник