Найти вероятность что хотя бы один

Учебник по теории вероятностей

1.4. Сложение и умножение вероятностей

События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.

Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:

Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:

Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.

Примеры решений задач с событиями

Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика,
;

— вынули черный шар из первого ящика,
;

В – белый шар из второго ящика,
;

— черный шар из второго ящика,
.

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей
, .
Тогда искомая вероятность по теореме сложения будет
.

Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.

Пусть А – попадание первого стрелка, ;

В – попадание второго стрелка, .

Тогда — промах первого, ;

— промах второго, .

Найдем нужные вероятности.

а) АВ – двойное попадание,

б) – двойной промах, .

в) А+В – хотя бы одно попадание,

.

г) – одно попадание,

.

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

2. .

3.

Вероятность наступления хотя бы одного события

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?

Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Примеры решений на эту тему

Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события (попадание первого орудия), (попадание второго орудия) и (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям , и (т. е. вероятности промахов), соответственно равны:

, ,

Искомая вероятность .

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События «машина работает» и «машина не работает» (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице:

Отсюда вероятность того, что машина в данный момент не работает, равна

Искомая вероятность

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие «при n выстрелах стрелок попадает в цель хотя бы один раз». События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .

Приняв во внимание, что, по условию, (следовательно, ), получим

Прологарифмируем это неравенство по основанию 10:

Итак, , т.е. стрелок должен произвести не менее 5 выстрелов.

Источник

Вероятность появления хотя бы одного события

$P\left( A \right) = 1 — P\left( <\bar A>\right) = 1 — \cdot\cdot \ldots \cdot$

где q — вероятность наступления события, противоположного событию A

Пример 1
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,02 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
q₁ — вероятность неисправности первого платёжного автомата;
q₂ — вероятность неисправности второго платёжного автомата.
Искомая вероятность равна:

P=1–0.02·0.02=0.9996

Пример 2

Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.

Решение

А — «стрелки получат приз». Из условия задачи вероятность попадания равна р=0.3, следовательно вероятность их промаха

q=1–р=1–0,3=0,7

Отсюда искомая вероятность равна

P(A)=1–q 4 =1–0,7 4 =

=1–0,2401=0,7599

Пример 3
Вероятность попадания при одном выстреле в мишень 0,7. Найдите вероятность хотя бы одного попадания при 4 выстрелах.
Решение

q=1–р=1–0,7=0,3

P(A)=1–q 4 =1–0,3 4 =

=1–0,0081=0,9919

Пример 4
Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Решение
А — «устройство не работает»
A₁ — «отказал первый элемент»
A₂ — «отказал второй элемент»
Найдём вероятности безотказной работы независимых элементов
q₁=1-0,05=0,95,
q₂=1-0,08=0,92
Следовательно, вероятность того, что устройство не работает равна

==1-0,874=0,126

Пример 6

Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,5; 0,6

Решение

A₁=0.3, A₂=0.4, A₃=0.5, A₄=0.6 из условия задачи.
Воспользуемся формулой:

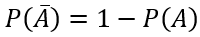
Находим соответствующие им вероятности

Р($\overline <>$) = 1 — 0,4 = 0,6

Р($\overline <>$) = 1 — 0,5 = 0,5

Р($\overline <>$) = 1-0,6 = 0,4

Из условия задачи события A₁, A₂, A₃ и A₄ независимы, следовательно получаем

Источник

Решение задач с формулировкой «хотя бы один»

Поговорим о задачах, в которых встречается фраза «хотя бы один». Наверняка вы встречали такие задачи в домашних и контрольных работах, а теперь узнаете, как их решать. Сначала я расскажу об общем правиле, а потом рассмотрим частный случай независимых событий и схемы Бернулли, выпишем формулы и примеры для каждого.

Общая методика и примеры

Общая методика для решения задач, в которых встречается фраза «хотя бы один» такая:

А теперь разберем ее на примерах. Вперед!

Пример 1. В ящике находится 25 стандартных и 6 бракованных однотипных деталей. Какова вероятность того, что среди трёх наудачу выбранных деталей окажется хотя бы одна бракованная?

Действуем прямо по пунктам.
1. Записываем событие, вероятность которого надо найти прямо из условия задачи:
$A$ =(Из 3 выбранных деталей хотя бы одна бракованная).

Для первого примера запишем решение подробно, далее будем уже сокращать (а полные инструкции и калькуляторы вы найдете по ссылке выше).

4. Тогда искомая вероятность:

Пример 2. Из колоды в 36 карт берут наудачу 6 карт. Найти вероятность того, что среди взятых карт будут: хотя бы две пики.

4. Тогда искомая вероятность:

Пример 3. В урне 2 белых, 3 черных и 5 красных шаров. Три шара вынимают наугад. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета.

4. Искомая вероятность:

Частный случай. Независимые события

Идем дальше, и приходим к классу задач, где рассматривается несколько независимых событий (стрелки попадают, лампочки перегорают, машины заводятся, рабочие болеют с разной вероятностью каждый и т.п.) и нужно «найти вероятность наступления хотя бы одного события». В вариациях это может звучать так «найти вероятность, что хотя бы один стрелок из трех попадет в цель», «найти вероятность того, что хотя бы один автобус из двух вовремя приедет на вокзал», «найти вероятность, что хотя бы один элемент в устройстве из четырех элементов откажет за год» и т.д.

Если в примерах выше речь шла о применении формулы классической вероятности, здесь мы приходим к алгебре событий, используем формулы сложения и умножения вероятностей (небольшая теория тут).

Пример 4. Узел содержит две независимо работающие детали. Вероятности отказа деталей соответственно равны 0,05 и 0,08. Найти вероятность отказа узла, если для этого достаточно, чтобы отказала хотя бы одна деталь.

Действуем аналогично. Рассмотрим основное событие
$A$ =(Формула содержится хотя бы в одном справочнике). Введем независимые события:
$A_1$ = (Формула есть в первом справочнике),
$A_2$ = (Формула есть во втором справочнике),
$A_3$ = (Формула есть в третьем справочнике).

Пример 6. Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение смены первый станок потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвёртый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.

Думаю, вы уже уловили принцип решения, вопрос только в количестве событий, но и оно не оказывает влияния на сложность решения (в отличие от общих задач на сложение и умножение вероятностей). Только будьте внимательны, вероятности указаны для «потребует внимания», а вот вопрос задачи «хотя бы один станок НЕ потребует внимания». Вводить события нужно такие же, как и основное (в данном случае, с НЕ), чтобы пользоваться общей формулой (1).

Ответ: 0,982. Почти наверняка мастер будет отдыхать всю смену;)

Частный случай. Повторные испытания

Думаете, дальше будет сложнее? Напротив, случаи все более частные, решения и формулы все более простые.

Подробнее о схеме Бернулли можно прочитать в онлайн-учебнике, а также посмотреть статьи-калькуляторы о решении различных подтипов задач (о выстрелах, лотерейных билетах и т.п.). Ниже же будут разобраны задачи только с «хотя бы один».

Пример 7. Пусть вероятность того, что телевизор не потребует ремонта в течение гарантийного срока, равна 0,9. Найти вероятность того, что в течение гарантийного срока из 3 телевизоров хотя бы один не потребует ремонта.

Пример 8. Производится 5 независимых выстрелов по некоторой цели. Вероятность попадания при одном выстреле равна 0,8. Найти вероятность того, что будет хотя бы одно попадание.

Думаю, с применением формулы (2) все более чем ясно (не забудьте почитать и о других задачах, решаемых в рамках схемы Бернулли, ссылки были выше). А ниже я приведу чуть более сложную задачу. Такие задачи встречаются пореже, но и их способ решения надо усвоить. Поехали!

Пример 9. Производится n независимых опытов, в каждом из которых некоторое событие A появляется с вероятностью 0,7. Сколько нужно сделать опытов для того, чтобы с вероятностью 0,95 гарантировать хотя бы одно появление события A?

Округляя, получаем что нужно провести не менее 3 опытов.

Ответ: минимально нужно сделать 3 опыта.

Полезные ссылки

Источник

20. Вероятность появления хотя бы одного события

В жизни, производстве часто возникают такие ситуации, когда нужно вычислить вероятность появления хотя бы одного события из некоторого набора возможных событий. Например, если по цели был сделан залп из нескольких орудий, то интерес представляет вероятность того, что цель будет поражена, т. е. что будет хотя бы одно попадание.

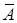
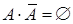
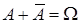
Два несовместных события A и называются противоположными, если при эксперименте одно из них обязательно произойдет. Иначе, для противоположных событий справедливы равенства:

, .

Вероятности противоположных событий связаны соотношением

(18.1)

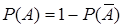
Вероятность появления хотя бы одного из событий A1, A2,…, An равна разности между единицей и вероятности совместного появления противоположных событий:

. (18.2)

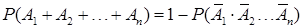
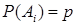
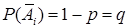
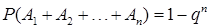
Если события A1, A2,…, An независимы и их вероятности одинаковы, т. е. и , то

. (18.3)

Пример 18.1. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1=0,8, p2=0,7, p3=0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Решение. Поскольку вероятности попаданий независимы и q1=1–p1=0,2, q2=1–p2=0,3, q3=1–p3=0,1, то искомая вероятность равна

P(A) = 1–q1q2q3 = 1–0,006 = 0,994.

Пример 18.2. Уличный торговец предлагает прохожим иллюстрированную книгу. Из предыдущего опыта ему известно, что в среднем один из 65 прохожих, которым он предлагает книгу, покупают ее. В течение некоторого промежутка времени он предложил книгу 20 прохожим. Чему равна вероятность того, что он продаст им хотя бы одну книгу?

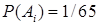
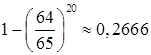
Решение. Пусть Ai – событие того, что i-й прохожий купит книгу. Вероятность этого события , а противоположного события . Тогда вероятность того, что хотя бы один из 20 прохожих купят книгу, будет равна

.

Пример 18.3. Вероятность того, что при одном выстреле стрелок попадет в цель, равна p=0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Вероятность попадания хотя бы один раз при n выстрелах равна:

Где q=1–p. Поскольку P(A)³0,9, то

1 – qn ³ 0,9 Þ qn £ 0,1 Þ n lg q £ lg0,1 Þ

.

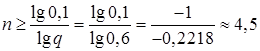
Таким образом, чтобы хотя бы один раз попасть в цель с вероятностью не менее 0,9, стрелок должен произвести не менее 5 выстрелов.

18.1. Отдел маркетинга фирмы проводит опрос для выяснения мнений потребителей по определенному типу продуктов. Известно, что в местности, где проводятся исследования, 10% населения являются потребителями интересующего фирму продукта и могут дать ему квалифицированную оценку. Компания случайным образом отбирает 10 человек из всего населения. Чему равна вероятность того, что, по крайней мере, один человек из них может квалифицированно оценить продукт?

Ответ. .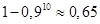

18.2. Пакеты акций, имеющихся на рынке ценных бумаг, могут дать доход владельцу с вероятностью 0,5 (для каждого пакета). Сколько пакетов акций различных фирм нужно приобрести, чтобы с вероятностью, не меньшей 0,96875, можно было ожидать доход хотя бы по одному пакету акций?

Ответ. Из уравнения 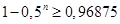получаем, что не менее 5 пакетов.

18.3. Для рыночного исследования необходимо проведение интервью с людьми, которые добираются на работу общественным транспортом. В районе, где проводится исследование, 75% людей добираются на работу общественным транспортом. Если три человека согласны дать интервью, то чему равна вероятность того, что, по крайней мере, один из них добирается на работу общественным транспортом?

Ответ. .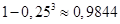

18.4. Модельер, разрабатывающий новую коллекцию одежды к весеннему сезону, создает модели в зеленой, черной и красной цветовой гамме. Вероятность того, что зеленый цвет будет в моде весной, модельер оценивает в 0,3, что черный – в 0,2, а вероятность того, что будет моден красный цвет – в 0,15. Предполагая, что цвета выбираются независимо друг от друга, оцените вероятность того, что цветовое решение коллекции будет удачным хотя бы по одному из выбранных цветов?

Ответ. P=1 – 0,7×0,8×0,85 = 0,524

18.5. Предположим, что для одной торпеды попасть в цель равна 0,7. Какова вероятность того, что три торпеды потопят корабль, если для потопления корабля достаточно одного попадания в цель?

Ответ. .

Источник