Назовите ученого доказавшего что угол вписанный в полуокружность прямой
Назовите ученого, доказавшего, что угол, вписанный в полуокружность — прямой?
Не иначе, это Евклид. Вроде как свойства треугольника и окружности ещё в его «Началах» излагались с должной подробностью.
Можно. Сложи квадрат, и положи перпендикулярно пятую спичку по середине
Теперь вычитаем четверку из 10, получаем 6, из 6 вычитаем 4/√3 или 4√3/3.
Задача это легко решается «на пальцах», так как ответ надо выбрать из нескольких имеющихся.
Таким образом, угол между биссектрисами вертикальных углов в два раза больше угла между смежными углами. Но хочется заметить, что вышеприведенные рассуждения не являются строгим математическим доказательством этого факта. Поэтому по уму надо еще приводить доказательство, что это так. Но мы должны ответить на вопрос в тесте. Поэтому отвечаем:
Для облицовки плиткой внешних углов имеется три варианта:
Угол между плоскостями MAB и MAD равен углу между сторонами ромба АВ и AD.
Учитывая, что из равенства диагонали BD стороне ромба следует равносторонность треугольников ABD и BCD, то есть угол BAD равен шестидесяти градусам, то и угол между плоскостями MAB и MAD тоже равен шестидесяти градусам
Теорема о вписанном угле
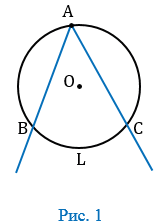
На рисунке 1 угол ВАС вписанный, дуга ВLС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу ВLC.
Теорема
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Доказательство
Доказать: 
АВС = 
АС.
Доказательство:
Луч ВО совпадает с одной из сторон угла АВС.
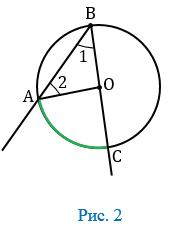
Пусть ВО совпадает с ВС (Рис. 2).
В данном случае дуга АС меньше полуокружности, следовательно, АОС =АС (т.к. АОС — центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
Луч ВО делит угол АВС на два угла.
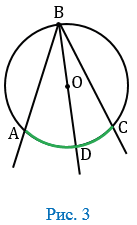
В данном случае луч ВО пересекает дугу АС в некоторой точке D (Рис. 3).
Точка D разделят дугу АС на две дуги: АD и DС, поэтому АС = АD + DС.
Луч ВD разделяет угол АВС на два угла, поэтому АВС = АВD + DВС.
По доказанному в 1 случае АВD = АD и DВС = DС. Складывая эти равенства, получаем: АВD + DВС = АD + DС или АВD + DВС = (АD + DС). Следовательно, АВС = АС.
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
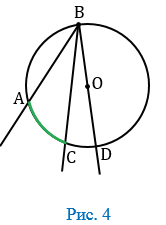
В данном случае луч ВС пересекает дугу АD в точке С (Рис. 4).
Луч ВС разделяет угол АВD на два угла, поэтому АВD = АВC + CВD, откуда АВC = АВD — CВD.
Теорема доказана.
Следствия из теоремы о вписанном угле
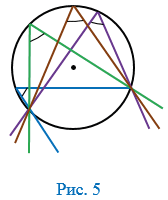
| 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис. 5). |
Теорема
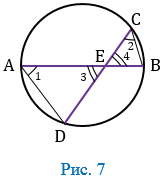
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Доказательство
Доказать: АЕ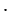
ВЕ = СЕDЕ.
Доказательство:
В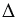 
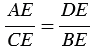
АDЕ и СВЕ: 1 = 2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле), 3 = 4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому 
, откуда АЕВЕ = СЕDЕ. Теорема доказана.
Теорема
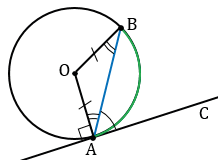
| Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. |
Доказательство
Доказать: ВАС = АВ.
Доказательство:
Поделись с друзьями в социальных сетях:
Вписанный угол окружности
Вписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.
Угол ABC — вписанный угол. ∠ABC опирается на дугу AC, заключённую между его сторонами.
Теорема о вписанном угле
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:
| ∠ABC = | 1 |  AC. |
| 2 |
При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.
Первый случай. Сторона вписанного угла проходит через центр окружности.
Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, ∠A = ∠B, как углы при основании равнобедренного треугольника.
Так как ∠AOC — внешний угол равнобедренного треугольника, то:
а так как углы A и B равны, то
Но ∠AOC — центральный угол, значит ∠AOC = AC, следовательно ∠B измеряется половиной дуги AC:
| ∠ABC = ∠B = | 1 | AC. |
| 2 |
Второй случай. Центр окружности лежит между сторонами вписанного угла.
Проведём диаметр BD. Угол ABC разбился на два угла: ∠1 и ∠2.
Точка D разделяет дугу AC на две дуги: AD и DC. По доказательству, рассмотренному в первом случае:
| ∠1 = | 1 | AD и ∠2 = | 1 | DC. |
| 2 | 2 |
Следовательно, весь угол ABC будет измеряться половиной дуги AC:
| ∠1 + ∠2 = | 1 | AD + | 1 | DC |
| 2 | 2 |
| ∠ABC = | 1 | AC. |
| 2 |
Третий случай. Центр окружности лежит вне вписанного угла.
Проведём диаметр BD.
| ∠ABC = | 1 | AC. |
| 2 |
Следствия из теоремы
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.
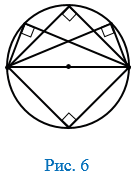
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности.
Половина окружности содержит 180°, значит, угол, опирающийся на диаметр, содержит 90°.
Вписанный угол, опирающийся на диаметр
Вписанный угол, опирающийся на диаметр, обладает полезным свойством, вытекающим из теоремы о вписанном угле.
Свойство вписанного угла, опирающегося на диаметр
(следствие из теоремы о вписанном угле)
Вписанный угол, опирающийся на диаметр, прямой.
Дано:
Так как AC- диаметр, то ∠AOC=180º.
∠AOC — центральный, ∠ABC — соответствующий ему вписанный угол.
Следовательно, по теореме о вписанном угле,
Что и требовалось доказать.
Из этого следует, например, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой.
Если центр описанной окружности лежит на диагонали четырехугольника, то угол напротив этой диагонали — прямой.
Другой вариант формулировки следствия:
Диаметр виден из любой точки окружности под углом 90º.
Если вписанный угол связать с дугой, то следствие из теоремы о вписанном угле звучит так:
Вписанный угол, опирающийся на полуокружность — прямой.
Теоретическое и методологическое обеспечение преподавания геометрии в 8-м классе по теме «Вписанный угол»
Разделы: Математика
Описанная технология не может применяться при изучении каждого определения – все зависит от уровня развития мышления школьников, их обученности. Подготовка к уроку начинается с логического и дидактического анализа формулировки определения, теоремы и способа доказательства (случай изучения теоремы).
Технология изучения определения понятия “Вписанный угол”
Определение: //Угол//, //вершина которого лежит на окружности//, а //стороны пересекают окружность//, //называется вписанным углом//.
1. Анализ формулировки
а) Определение дано через род и видовые отличия
б) Родовое понятие: угол
1) Вершина лежит на окружности
2) Каждая сторона пересекает окружность
в) Содержание: конъюнктивная структура
Объем понятия: множество всех углов вписанных во все (в каждую) окружности.
2. Существование можно доказать построением.
3. Переформулирование: не возможно.
4. Частные эвристики.
1.1 Чтобы доказать, что угол является вписанным в окружность, необходимо доказать, что вершина угла лежит на окружности, а стороны пересекают окружность.
1.2 Чтобы доказать, что вершина угла лежит на окружности, а стороны пересекают окружность, необходимо доказать, что угол является вписанным в окружность.
2.1 Если угол является вписанным в окружность, то вершина угла лежит на окружности, а стороны пересекают окружность.
2.2 Если вершина угла лежит на окружности, а стороны пересекают окружность, то угол является вписанным в окружность.
5. Составление отрицания определения.
Угол не является вписанным в окружность, если вершина угла не лежит на окружности или стороны угла не пересекают окружность.
6. Установление связи между новым понятием и изученным ранее
Фрагмент урока по изучению определения вписанного угла
| Учитель | Ученик |
| I. Мотивационно-ориентировочная часть Актуализация | |
| На прошлом уроке геометрии мы изучили такое геометрическое понятие, как центральный угол, повторили понятия окружности, дуги окружности. Давайте вспомним, что такое центральный угол? | Угол, вершина которого лежит в центре окружности, а стороны пересекают окружность называется центральным углом. |
| Так, а теперь начертим три окружности с произвольным радиусом и внутри этих окружностей построим углы, причем все они должны быть расположены по-разному. |  |
| Давайте рассмотрим и проанализируем эти три угла: угол 1 – центральный, а угол 2 и угол 3 – что вы можете сказать о них. Где находится вершина угла 2?, угла 3? | Вершина угла 2 находится внутри окружности, а вершина угла 3 лежит на окружности. |
| А что можно сказать о расположении сторон угла 2 и 3? | Стороны угла 2 и 3 будут пересекать данную окружность |
| Тогда где же будет находиться угол? | Внутри |
| А теперь давайте, конкретизируем ваши ответы, то есть возьмем угол 3 и рассмотрим частные характеристики этого угла. Что можно сказать? | – вершина угла 3 лежит на окружности; – стороны пересекают окружность; – угол 3 находится внутри окружности. |
| Хорошо, а можем ли мы сказать, что угол 3 вписан в окружность? | Да |
| Как вы думаете, какая тема сегодняшнего урока? | Угол, вписанный в окружность |
| Да, но конкретнее сказать “Вписанный угол”. Какая же учебная задача стоит сегодня перед нами? | Дать определение вписанного угла и установить его свойства. |
| Подумайте и ответьте самостоятельно на вопрос, что же такое вписанный угол? | Угол, вершина которого лежит на окружности, а стороны пересекают окружность. |
| Да, верно. Начнем с темы “Вписанный угол” и учебная задача – сформулировать определение вписанного угла. | |
II. Операционно-познавательная (содержательная) часть.
Учитель: Давайте построим еще три окружности с произвольными радиусами. Теперь поставим произвольные точки, так чтобы они были расположены в различных местах на окружности – они будут являться вершинами углов, из этих точек выпустим по два луча, пересекающие окружность в двух точках.
 |  |  |
Давайте проанализируем эти окружности и запишем результаты по рисункам. Что можно сказать по рис.№1?
Ученики: Дана окружность и угол ABC:
а) вершина угла ABC точка B лежит на окружности;
б) стороны угла ABC пересекают окружность в точках A и C соответственно;
в) угол ABC опирается на дугу AC,
отсюда можно сделать вывод, что на этом рис.№1 угол ABC – вписанный угол. Углы с рисунков №2 и №3 также являются вписанными, потому что названные выше аспекты подходят к этим углам.
Учитель: Какой же общий итог можно подвести по всем трем рисункам?
Ученики: На всех трех рисунках изображены вписанные углы, в независимости от их расположения.
Учитель: Хорошо, а теперь давайте вместе, обобщив полученные данные, сформулируем определение вписанного угла.
Ученики: Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Учитель: Так, а теперь я хотела бы вам немного усложнить задачу. Что изображено на данном рисунке?
Ученики: Дана окружность, два вписанных угла, которые опираются на одну и ту же дугу.
Учитель: А как вы определили, что эти углы вписанные?
Ученики: Так как вершины углов лежат на окружности, а стороны углов пересекают окружность и оба они опираются на одну и ту же дугу.
Учитель: Хорошо, а теперь давайте возьмем транспортир и измерим оба этих угла и скажите полученный результат
Ученики: Вписанные углы, опирающиеся на одну и ту же дугу, равны
Учитель: Хорошо, с этой задачей вы справились успешно, но теперь я бы хотела предложить вам еще одну задачу:
Что вы видите на этом рисунке?
Ученики: Дана окружность, в окружность вписан угол MNR, он опирается на дугу MR – она является полуокружностью.
Учитель: Теперь измерьте данный угол MNR.
Ученики: Вписанный угол, опирающийся на полуокружность – прямой.
Учитель: Итак, посмотрите, оказывается, сколько частных эвристик вписанного угла мы с вами сегодня открыли. А теперь давайте запишем понятия, которые мы с вами определили:
1. Определение вписанного угла;
2. Вписанные углы, опирающиеся на одну и ту же дугу равны.
3. Вписанный угол, опирающийся на полуокружность – прямой.
III. Рефлексивно – оценочная часть
Учитель: Какая учебная задача стояла перед нами? Достигли ли мы ее?
Ученики: Да, мы сформулировали определение вписанного угла.
Учитель: Чтобы легче запомнить определение выделим его существенные части: угол, вершина которого лежит на окружности, а стороны пересекают окружность
Учитель: Какой новый изученный термин появился?
Ученики: Вписанный угол
Учитель: В каком случае говорят, что угол является вписанным?
Ученики: Если вершина лежит на окружности, а стороны пересекают окружность.
Учитель: Так, а теперь договоримся обозначать вписанные углы также как и обычные, то есть угол ABC или угол B (по вершине угла)
После этого можно предложить учащимся упражнения на распознавание вписанных углов (подведение под понятие)
Выберите вписанные углы. Ответ обоснуйте.
Углы ABC(№1), MNK(№3),DRQ(№6) – вписанные, так как вершины этих углов лежат на окружности, а стороны пересекают окружность;
Угол AOC(№2) – не вписанный, так как его вершина не лежит на окружности, угол AOC – центральный (по определению);
Угол RPC(№4) – не вписанный, так как его вершина (так же как на рис.№2) не лежит на окружности;
Угол MRK (№5) – не вписанный, так как его стороны не пересекают окружность.
Учитель: Так, а теперь давайте подведем итоги нашего урока и сделаем выводы.
Ученики: Мы узнали, что такое вписанный угол и по каким признакам можно выделить этот угол среди остальных углов, то есть угол, вершина которого лежит на окружности, а стороны пересекают окружность, кроме того мы рассмотрели частные случаи вписанного угла:
1. вписанные углы, опирающиеся на одну и ту же дугу равны;
2. вписанный угол, опирающийся на полуокружность – прямой
Технология изучения теоремы
Теорема об измерении вписанного угла
Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается.
Пусть угол АВС – вписанный угол окружности с центром О, опирающийся на дугу АС. Докажем что, АВС = ½ дуги АС. Рассмотрим три возможных случая расположения луча ВО относительно угла АВС.
I. Анализ формулировки
Формулировка теоремы носит условную форму, она записана в словесной форме.
– Условие: Вписанный угол
– Заключение: Измеряется половиной дуги, на которую он опирается.
Теорема простая, так как ее условие состоит из 1-ой части и заключения.
II. Логический смысл теоремы
Теорема выражает свойство вписанного угла, которое позволяет, с одой стороны измерять вписанный угол, с другой стороны измерять дугу, на которую он опирается.
III. Формулировка обратного, противоположного и противоположного обратному предложений.
Сформулировать однозначно обратное утверждение нельзя. В частном случае:
IV. Анализ доказательства
Общая идея доказательства сводится к доказательству равенства углов треугольника. Доказательство методом полной индукции. Теоретический базис доказательства состоит из определения вписанного угла, равенства углов треугольника.
V. Исследование математической ситуации, рассмотрение всех возможных случаев
В доказательстве теоремы приведены 3 возможных случая расположения луча ВО относительно 
АВС, но сводящееся в теореме к равенству АВС = ½ дуги АС.
Три частных случая расположения луча ВО:
Рассматриваемая теорема “порождает” следствия:
VI. Установление связи теоремы с ранее изученным, ее роль в построении курса.
Теорема применяется для нахождения градусной меры вписанного угла, на комбинации окружности и многоугольника (вписанного в окружность), а это в свою очередь находит применение при решении задач.
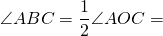
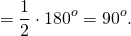
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность. В данном случае: угол ABC, вершина угла ABC – точка B лежит на окружности, а его стороны BA и BC пересекают окружность в точках A и C соответственно; угол ABC опирается на дугу AC.
