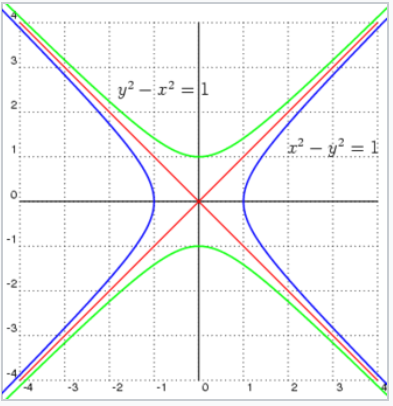
К чему стремится гипербола
Гипербола и её свойства
Гипербола и её форма.
Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac
$$
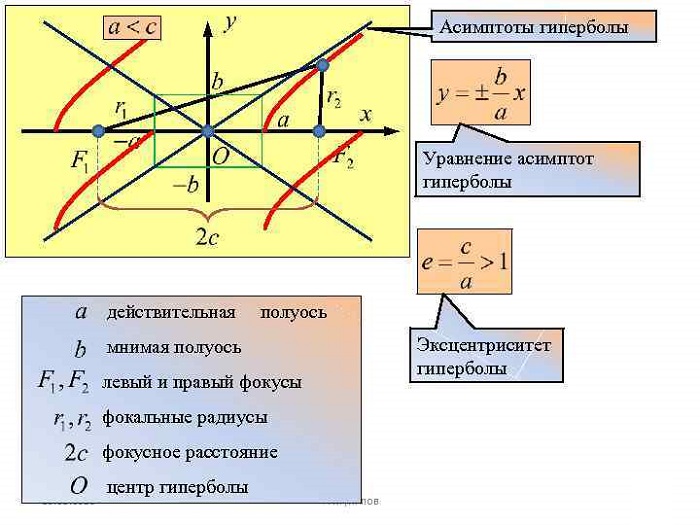
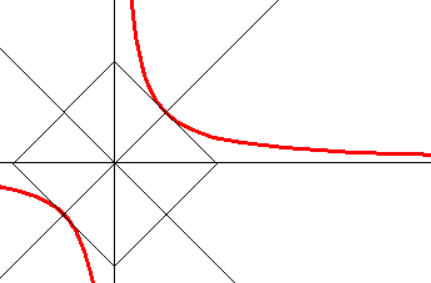
Из этого уравнения видно, что для всех точек гиперболы \(|x| \geq a\), то есть все точки гиперболы лежат вне вертикальной полосы ширины \(2a\) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами \((a, 0)\) и \((-a, 0)\), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа \(a\) и \(b\) называются соответственно вещественной и мнимой полуосями гиперболы.
Рис. 8.6. Гипербола.
Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.
Доказательство аналогично доказательству соответствующего утверждения для эллипса.
Рис. 8.7. Пересечение прямой и гиперболы.
Числитель дроби \(ab/v\) постоянен, а знаменатель принимает наибольшее значение при \(k=0\). Следовательно, наименьшую абсциссу имеет вершина \((a, 0)\). С ростом \(k\) знаменатель убывает, и \(x\) растет, стремясь к бесконечности, когда \(k\) приближается к числу \(b/a\). Прямая \(y=bx/a\) с угловым коэффициентом \(b/a\) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.
Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то \(k\) будет убывать, \(k^<2>\) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом \(-b/a\).
К прямой \(y=-bx/a\) относится все, что было сказано о \(y=bx/a\): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.
Прямые с уравнениями \(y=bx/a\) и \(y=-bx/a\) в канонической системе координат называются асимптотами гиперболы.
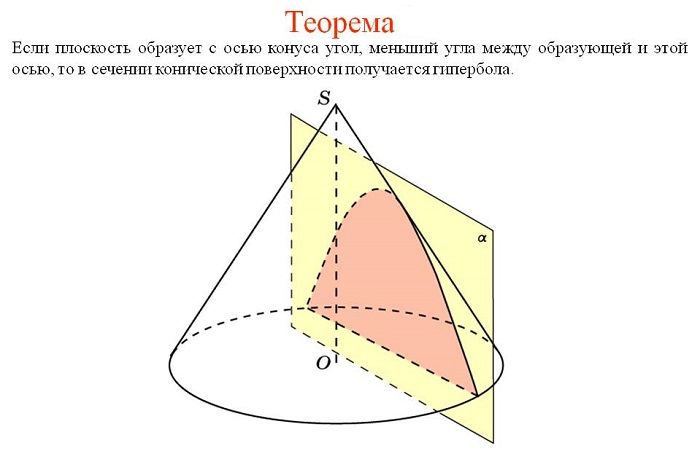
Перед вами родственные кривые, полученные при сечении конуса плоскостью. Парабола, эллипс (окружность), гипербола.
Что такое гипербола в математике
Это геометрическое место точек M, физическая разница расстояний от которых до выбранных (F1, F2), называемых фокусами, постоянна.
Оговоримся, что все сказанное относится к Евклидовой плоскости, где параллельные прямые не пересекаются.
Но если из отрезка |F1F2| соорудить координатную прямую X, за начальную точку взять середину (она же будет центром гиперболы) отрезка, то получим декартову систему координат. Где кривая описывается алгебраическим уравнением II-го порядка.
Получим классическую формулу аналитической геометрии:
где a – действительная полуось, b – мнимая.
поскольку x и y связаны квадратной зависимостью, обе оси будут осями симметрии;
пересечения с осью абсцисс (фокусов) с координатами ±a называются вершинами гиперболы, и расстояние между ними является минимальной дистанцией между ветвями (о последних ниже);
кратчайший отрезок от фокуса до вершины зовется перицентрическим расстоянием и пишется «rp».
Асимптоты и фокусы гиперболы
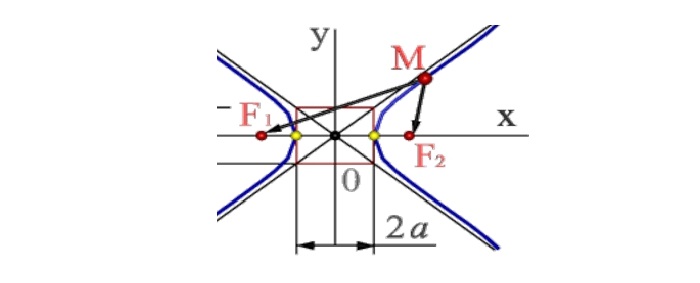
Фокусы находятся на оси X (из этого исходили). Расстояние до центра гиперболы (он же центр симметрии C) называется фокальным и обозначается «c». Его формула:
Умозрительно очевидно, что сечение конуса состоит из двух кривых. Называются они ветвями гиперболы. Также не подлежит сомнению то, что ветви ограничены воображаемой поверхностью. Фокусы всегда находятся внутри ветвей.
Помучившись с производными и пределами, получим формулы асимптот (прямые, расстояние до которых от кривой стремится к нулю на бесконечном удалении от «0»):
Дистанцию от фокуса до асимптоты зовут прицельным параметром и обозначают буквой «b».

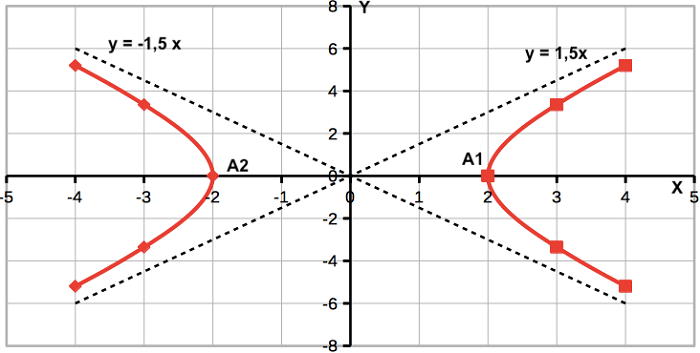
Как построить график функции гиперболы
Существует много ресурсов, где можно онлайн наблюдать, как строится функция. Но нужно все уметь самому. Итак, давайте учиться.
Построим для примера график уравнения
По формуле выше выстраиваем асимптоты.
Отмечаем вершины х = ±2 (А1, А2). Приблизительный вид уже ясен.
При х = ±3, y = ±3,5 (примерно).
Эксцентриситет гиперболы
Эксцентриситетом считают величину:
Является параметром, характеризующим отклонение конического сечения от окружности:
кривые с равным эксцентриситетом подобны;
показатель угла наклона асимптот.
Равнобочная (равносторонняя) гипербола
Таковой кривая является при условии a = b. Если покрутить систему координат, функцию можно свести к виду:
Эксцентриситет данной конструкции составит квадратный корень из 2.
Иначе говоря, получаем график обратной пропорциональности:
Или «любимую» школьниками.
Коль уж речь зашла о школьном курсе, добавим сведений:
прямые x = 0, y = 0 – асимптоты;
область определения – все действительные числа, кроме 0;
область значений – все, за исключением 0;
функция нечетная, поскольку меняет знак при смене знака аргумента;
убывающая при положительных и отрицательных x.
Касательная и нормаль
В каждой точке гладкой кривой возможно построить касательную и нормаль (перпендикуляр). Гипербола – не исключение. Касательная – прямая, совпадающая с кривой только в одной точке (в пределах изгиба одного порядка).
Уравнение касательной в точке с координатами (x0y0) имеет вид:
Сопряженные гиперболы
Записанное таким образом уравнение даст сопряженную фигуру:
То есть с теми же асимптотами, но расположенную по-другому, с поворотом на 90°.
Свойства гиперболы
Их должен знать каждый школьник:
Касательная в произвольной точке H окажется биссектрисой угла F1HF2.
Кривая симметрична относительно осей и своего центра.
Отсеченный асимптотами отрезок касательной делится точкой соприкосновения пополам. Площадь же выделенного треугольника не меняется от изменения точки.
Использование
Где применяются знания о гиперболе:
для создания эллиптических и других координат;
в солнечных часах (сечение конуса света);
для анализа движения космических объектов.
Заключение
Непростая кривая с неожиданными в некоторых случаях применением. Что удивительно, задача о сечениях конуса была поставлена древнегреческими учеными во II-м веке до нашей эры. Это говорит о высочайшем уровне тогдашних инженеров.
Нет, солнечные часы понятно были, а мелких искусственных спутников не было точно. И астероиды не исследовали, но вопросы возникали. И были ответы без ссылок на многочисленных богов. Удивительные люди.

Гипербола. График функции и свойства.
теория по математике 📈 функции
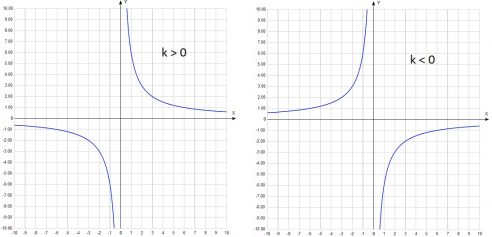
Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
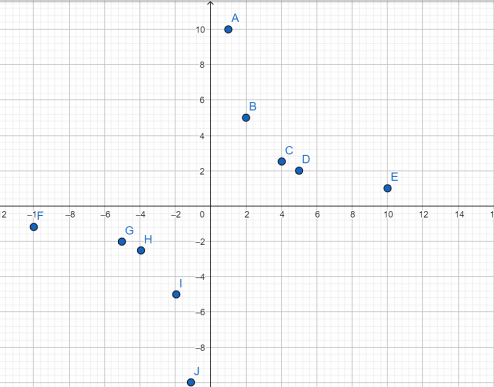
Установите соответствие между графиками функций и формулами, которые их задают.

Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Гипербола: определение, функция, формула, примеры построения
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Пример 1
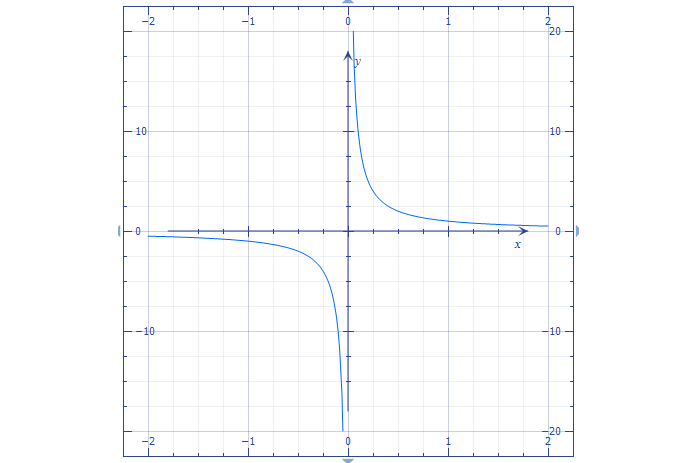
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>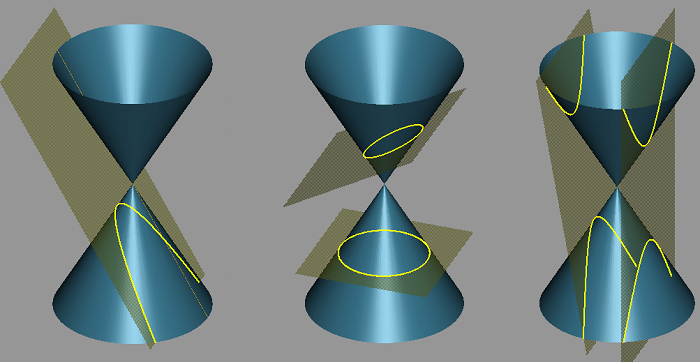
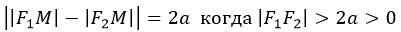
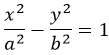
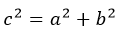
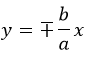
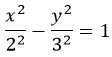
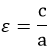
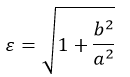
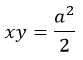
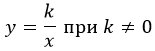
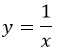
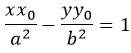
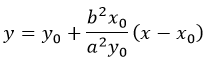
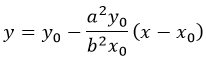
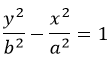




 гипербола, где k y≠0 это вторая асимптота.
гипербола, где k y≠0 это вторая асимптота. 







