Как доказать что 4 точки лежат в одной плоскости с координатами

Определить, насколько точно 4 точки лежат в плоскости

Дано 4 точки в пространстве. Требуется определить, насколько хорошо они ложатся в одну (неизвестную) плоскость.

Сразу не подходит вариант в духе «провести плоскость через 3 точки и посмотреть расстояние до 4й», так как мера должна быть как минимум симметричной и оптимальная плоскость вовсе не обязана проходить именно через первые 3 точки.

Рассматривал вариант с построением средней плоскости через линейную регрессию и дальше расчётом максимального расстояния до неё, но суть в том, что сама-то плоскость мне не нужна. В идеале не хотелось бы на её расчёт вычислительное время тратить.

Ещё, может, какие-нибудь предложения будут?

UPD: пока писал пост, придумал вариант с расчётом объёма тетраэдра, построенного на этих 4х точках через смешанное произведение. Вроде же норм?

Подсказка: Через четыре точки, не лежащие в одной плоскости, можно провести сферу.

Suslik
> пока писал пост, придумал вариант с расчётом объёма тетраэдра, построенного на этих 4х точках через смешанное произведение. Вроде же норм?
Тоже сразу подумал про объем тетраэдра.
Однако чистый объем умножает ошибку положения плоскости на площадь треугольника в основании — надо как-то нормировать. В принципе, можно посчитать минимальную высоту тетраэдра путем перебора пар фич.

>:+()___ [Smile]
> Однако чистый объем умножает ошибку положения плоскости на площадь треугольника
> в основании — надо как-то нормировать. В принципе, можно посчитать минимальную
> высоту тетраэдра путем перебора пар фич.
я думал взять кубический корень объёма, чтобы получить примерную оценку его эквивалентного линейного размера. по идее мне не нужно абсолютное значение, мне нужно, чтобы оно только сравнивалось хорошо.

TelVolt
> И есть ли вообще возможность преполагать, что точки хотя бы примерно лежат в
> плоскости? Или они вполне могут, например, образовывать правильный тетраэдр?
они могут образовывать что угодно

Я бы еще посмотрел на вариант когда проверяются все 4 возможных плоскости и расстояние до оставшейся точки и как мера выбирается минимальное из получившихся четырёх расстояний.

Можно сделать два треугольника, а потом посмотреть угол между их нормалями.

Весьма важно отношение с размером конечно. Надо чётко понимать что требуется.
Четыре точки в виде пирамиды но с ребром размером миллиметр это хуже или лучше чем десятиметровый квадрат у которого одна точка выпадает от плоскости на сантиметр?
От ответа и критерий сильно зависит.

Suslik
> я думал взять кубический корень объёма, чтобы получить примерную оценку его эквивалентного линейного размера.
Тогда у тебя тетраэдр с основанием в квадратный километр и высотой в сантиметр будет много хуже, чем с основанием в квадратный сантиметр и той же высотой.

=A=L=X=
> проверяются все 4 возможных плоскости и расстояние до оставшейся точки
Еще все пары противолежащих ребер надо проверять.

>:+()___ [Smile]
> Еще все пары противолежащих ребер надо проверять.

Не понял зачем. Я просто предложил избавиться от ошибки когда плоскость через три близлежащие точки очень плохо соотносится с четвёртой далеко удалённой.
Собственно теперь я думаю достаточно даже 3 плоскости проверить. Все четыре необязательно вроде если в уме себе этот симплекс рисовать.

Suslik
> мера должна быть как минимум симметричной и оптимальная плоскость вовсе не
> обязана проходить именно через первые 3 точки.
Найти центр тяжести, затем вектор главную ось инерции (вокруг которой момент инерции максимален).
Оценивать сумму модулей DP3 векторов из ЦТ к точкам с нормализованным вектором-осью.

Правка:
Правильнее оценивать сумму не модулей, а квадратов.

Суслик, ты меня огорчаешь с каждым новым постом

> В идеале не хотелось бы на её расчёт вычислительное время тратить.

Источник

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

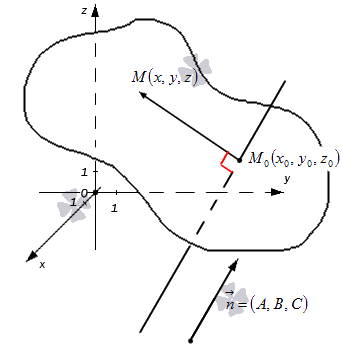
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Раскроем чуть шире смысл теорем.

Укажем пример как иллюстрацию этих утверждений.

Общее уравнение плоскости, проходящей через точку

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Решение

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Возможно получить это уравнение другим способом.

Решение

Рассмотрим два способа решения.

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

Неполное общее уравнение плоскости

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

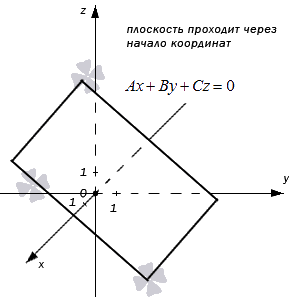
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

Р​​ешение

Задачу возможно решить еще одним способом.

Решение

Источник

Как доказать что 4 точки лежат в одной плоскости с координатами

Если три точки A, B и C лежат на одной прямой, то треугольник ABC обратится в отрезок прямой, а потому его площадь должна быть равна нулю. Полагая в формуле

S = 0, получим условие, при котором три точки лежат на одной прямой

В более удобной форме условие, при котором три точки лежат на одной прямой, можно записать так:

(1)

Подставляя сюда координаты данных точек, получим, что левая часть (1) будет равна

Требование (1) выполнено:

и, значит, три данные точки лежат на одной прямой.

Источник

Через три точки можно провести плоскость

Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Существование плоскости, проходящей через три данные точки

Существование плоскости, проходящей через три данные точки

Теорема 15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

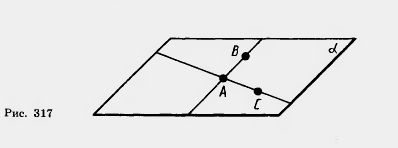
Доказательство. Пусть А, В, С — три данные точки, не лежащие на одной прямой (рис. 317). Проведем прямые АВ и АС; они различны, так как точки А, В, С не лежат на одной прямой. По аксиоме Сз через прямые АВ и АС можно провести плоскость . Эта плоскость содержит точки А, В, С.

Докажем, что плоскость а, проходящая через точки А, В, С, единственна. Действительно, плоскость, проходящая через точки А, В, С, по теореме 15.2 содержит прямые АВ и АС. А по аксиоме Сз такая плоскость единственна.

Задача (13). Можно ли провести плоскость через три точки, если они лежат на одной прямой? Объясните ответ.

Решение. Пусть А, В, С — три точки, лежащие на прямой . Возьмем точку D, не лежащую на прямой (аксиома I). Через точки А, В, D можно провести плоскость (теорема 15.3). Эта плоскость содержит две точки прямой — точки A и В, а значит, содержит и точку С этой прямой (теорема 15.2).

Следовательно, через три точки, лежащие на одной прямой, всегда можно провести плоскость.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

сколько плоскостей можно провести через

две различные точки

три различные точки

четыре точки никакие три из которых не лежат на одной прямой.

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

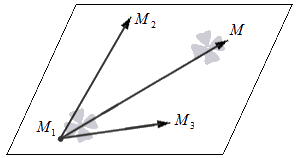
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1

На схеме это будет выглядеть так:

Запишем полученное уравнение в координатной форме:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Решение

Используем поочередно оба способа.

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73

Мы получили нужное нам уравнение.

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

Решение

Векторное произведение будет равно:

M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →

Если мы используем второй способ, у нас получится:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

Источник