Как доказать что биссектриса это биссектриса
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
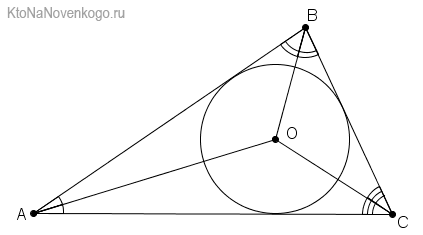
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Теорема о биссектрисе треугольника. Доказательство
Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:
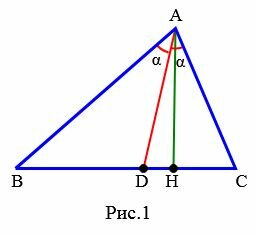 |
Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:
Построим следующее соотношение
С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:
Построим следующее соотношение используя формулы (6) и (7):
Из формул (5) и (8) получим соотношение (1).
Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).
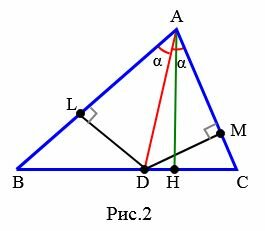 |
Тогда площади треугольников ABD и ACD можно найти из формул:
Построим следующее соотношение
Из формул (5) и (11) получим соотношение (1).
Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):
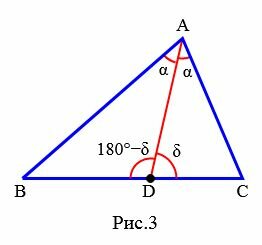 |
Применяя теорему синусов для треугольников ABD и ACD можем записать:
Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.
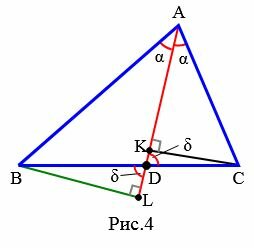 |
Из равенств (14) и (15) получаем:
Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.
Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:
Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:
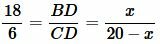 |
Методом перекресного умножения упростим (17) и решим:
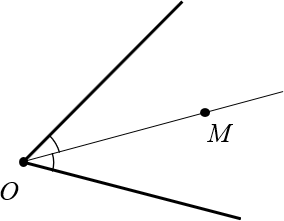
Биссектриса угла
Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.
Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек…
Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!
Биссектриса угла — коротко о главном
Биссектриса угла — это линия, делящая угол пополам.
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.
Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.
Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.
Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.
А теперь подробнее…
Определение биссектрисы угла
Помнишь шутку: «Биссектриса это крыса, которая бегает по углам и делит угол пополам»?
Так вот, настоящее определение биссектрисы угла очень похоже на эту шутку — биссектриса действительно делит пополам угол (а не отрезок, например):
Биссектриса угла – это линия, делящая угол пополам.
Или еще вот такое определение биссектрисы:
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
А вот определение биссектрисы треугольника:
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.
Биссектриса равнобедренного треугольника
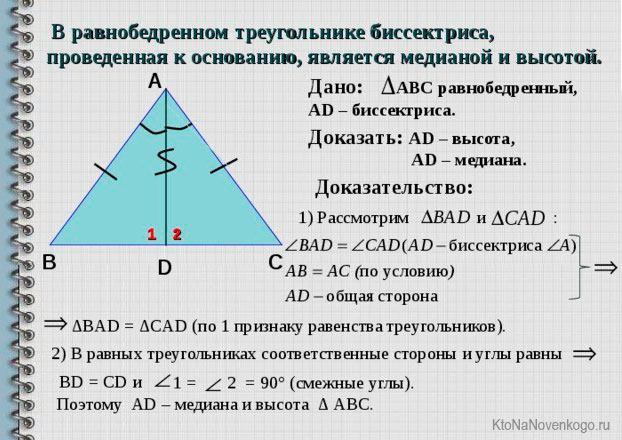
Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.
Но представляешь, это ещё не всё. Верна ещё и обратная теорема:
Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.
Мы скоро докажем обе этих теоремы, а пока твердо запомни:
Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!
Зачем же это твердо запоминать? Как это может помочь?
А вот представь, что у тебя задача:
Дано: \( AB=5,
Найти: \( \displaystyle BC. \)
Ты тут же соображаешь, \(\displaystyle BD \) биссектриса и, о чудо, она разделила сторону \( \displaystyle AC \) пополам! (по условию…).
Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.
Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!
Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике
Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?
Смотри: у \( \triangle ABL \) и \( \triangle CBL \) равны стороны \( AB \) и \( BC \), сторона \( BL \) у них вообще общая и \( \angle 1=\angle 2\). (\( BL \) – биссектриса!)
И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.
Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что \( \triangle ABL=\triangle CBL \), а значит \( AL \)= \( CL \) и \( \angle 3=\angle 4 \).
\( AL \) = \( CL \) – это уже хорошо – значит, \( BL \) оказалась медианой.
А вот что такое \( \angle 3=\angle 4 \)?
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Будет немного сложнее, но пока мы отвлечемся на термины — повторим что такое биссектриса, медиана и высота, чем они похожи и чем они отличаются.
Биссектриса, медиана, высота — определения и отличия
Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?
Если нет, не страшно. Сейчас разберемся.
Чем биссектриса, медиана и высота похожи между собой?
Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.
Чем биссектриса, медиана и высота отличаются между собой?
Вернемся к нашим баранам — к свойствам биссектрисы…
Угол между биссектрисами любого треугольника
B \( \triangle ABC \)проведем две биссектрисы \( AO \)и \( OC \).
Они пересеклись. Какой же угол получился у точки \( O \)?
Применим этот потрясающий факт. С одной стороны, из \( \triangle ABC \):
\( \angle A+\angle B+\angle C=180<>^\circ \), то есть \( \angle B=180<>^\circ \text< >-\text< >\left( \angle A+\angle C \right) \).
Теперь посмотрим на \( \triangle AOC \):
\( \angle 2+\angle 6+\angle 3=180<>^\circ \)
Но биссектрисы, биссектрисы же!
Значит \( \left( \triangle AOC \right) \)
Теперь через буквы
Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!
Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?
Биссектриса угла
Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.
Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.
И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)
Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:
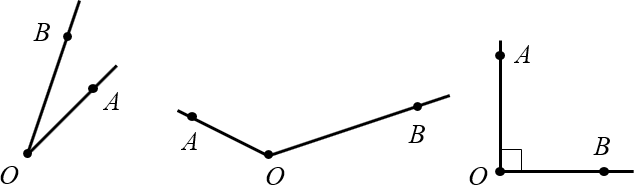
Определение. — это луч, который выходит из вершины этого угла и делит угол пополам.
Для приведённых выше углов биссектрисы будут выглядеть так:
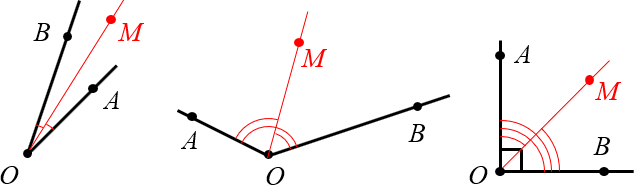
Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.
Основное свойство биссектрисы угла
На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:
Теорема. — это геометрическое место точек, равноудалённых от сторон данного угла.
В переводе с математического на русский это означает сразу два факта:
Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:
Определение. — это длина перпендикуляра, проведённого из данной точки к этой прямой.
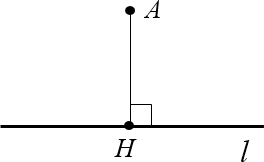
Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:
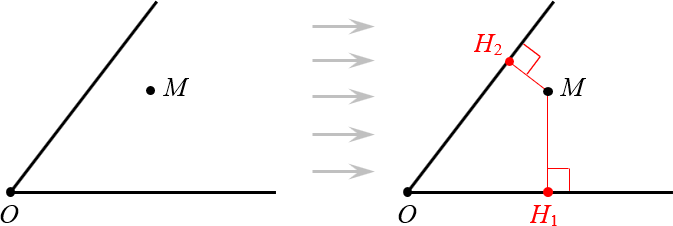
Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.
Как и обещал, разобьём доказательство на две части:
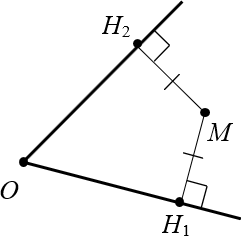
1. Расстояния от точки на биссектрисе до сторон угла одинаковы
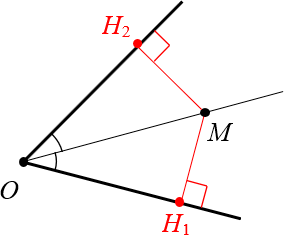
2. Если расстояния равны, то точка лежит на биссектрисе
В заключение доказательства отметим красными дугами образовавшиеся равные углы:
Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)
Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.
Биссектриса — это луч разрезающий угол пополам, а также отрезок в треугольнике обладающий рядом свойств
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком термине, как БИССЕКТРИСА.
Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.
Биссектриса — это.
Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.
Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.
Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам:
Само понятие БИССЕКТРИСА пришло к нам из латинского языка. И название это весьма говорящее. Оно состоит из двух слов – «bi» означает «двойное, пара», а «sectio» можно дословно перевести, как «разрезать, поделить».
Вот и получается, что само слово БИССЕКТРИСА – это «разрезание пополам», что собственно и отражается в определении термина, который мы только что привели.
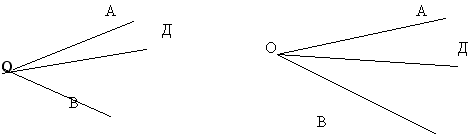
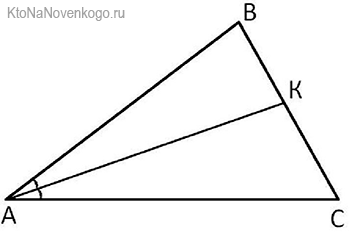
А сейчас задачка на закрепление материала. Посмотрите на эти рисунки и скажите, на каком изображена биссектриса. Подумали? Правильно, на втором.
На первом луч, выходящий из угла АОВ, явно не делит его пополам. На втором это соотношение углов более очевидно, а потому можно предположить, что луч ОД является БИССЕКТРИСОЙ. Хотя, конечно, на сто процентов это утверждать сложно.
Для более точного определения используют специальные инструменты. Например, транспортир. Это такой инструмент в виде полусферы из металла или пластмассы. Вот как он выглядит:
Хотя есть еще вот такие варианты:
Наверняка у каждого такие были в школе. И пользоваться ими весьма просто. Надо только ровненько совместить основание транспортира (прямоугольная линейка) с основанием треугольника, а после на полусфере отметить значение, которое соответствует размеру угла.
И точно по такой же схеме можно поступить наоборот – имея транспортир, начертить угол необходимого размера. Чаще всего – от 0 до 180 градусов. Но на втором рисунке у нас транспортир, который помогает начертить градусы от 0 до 360.
Количество биссектрис в треугольнике
Но вернемся к нашей главной теме. И ответим на вопрос – сколько БИССЕКТРИС есть в треугольнике?
Ответ в общем-то логичен, и он заложен в самом названии нашей геометрической фигуры. Треугольник – три угла. А соответственно, и биссектрис в нем будет тоже три – по одной на каждую вершину.
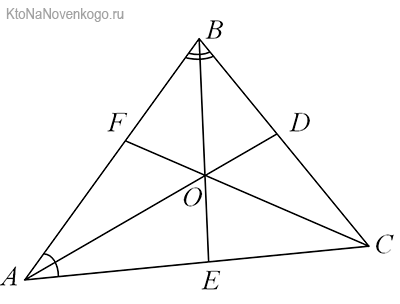
Снова посмотрим на наши рисунки. В данном случае наглядно видно, что у треугольника АВС (именно так в геометрии обозначается эта фигура – по наименованию ее вершин) три БИССЕКТРИСЫ. Это отрезки AD, BE и CF.
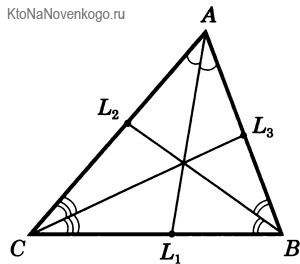
На чертежах БИССЕКТРИСЫ обозначатся следующим образом. Видите одинарные выгнутые черточки между отрезками АС /AL1 и АВ/AL1? Так обозначаются углы. А то, что они оба обозначены одинаковыми черточками, говорит о том, что углы равны. А значит, отрезок AL1 является БИССЕКТРИСОЙ.
То же самое относится и к углам между АВ/DL2 и ВС/BL2. Они обозначены одинаковыми двойными черточками. А значит, отрезок BL2 – биссектриса. А углы АС/CL3 и ВС/CL3 обозначены тройными черточками. Соответственно, это показывает, что отрезок CL3 также является биссектрисой.
Пересечение биссектрис треугольника
Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:
Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!
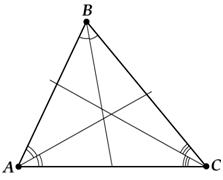
Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:
Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.
А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.
Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.
Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.
Свойство основания биссектрисы
У каждой БИССЕКТРИСЫ есть основание. Так называют точку пересечения со стороной треугольника. Например, в нашем случае это будет точка К.
И с этим основанием связана одна весьма интересная теорема. Она гласит, что
Биссектриса треугольника делит противоположную сторону, то есть точкой основания, на два отрезка. И их отношение равно отношению двух прилежащих сторон.
Звучит несколько тяжеловато, но на деле выглядит весьма просто. Отношение отрезков на основании биссектрисы – это ВК/КС. А отношение прилежащих сторон – это АВ/АС. И получается, что в нашем случае теорема выглядит вот так:
Интересно, что для данной теоремы будет справедливо и другое утверждение:
Ну, как часто бывает в математике – это правило работает и в обратном направлении. То есть, если вы знаете длины все сторон и их соотношения равны, то можно сделать вывод, что перед нами БИССЕКТРИСА, А соответственно, будет проще рассчитать размер угла треугольника.
Биссектриса равнобедренного треугольника
Для начала напомним, что такое равнобедренный треугольник.
Это такой треугольник, у которого две стороны абсолютно равны (то есть имеет равные «бедра»).
Так вот в таком треугольнике БИССЕКТРИСА имеет весьма интересные свойства.
Она одновременно является еще и медианой (что это?), и высотой.
Эти понятия нам также знакомы по школьному курсу. Но если кто забыл, мы обязательно напомним:
А в равностороннем треугольнике или как его еще называют правильном (у которого все стороны и все углы равны) все три биссектрисы являются высотами и медианами. И плюс ко всему, их длины равны.
Вот и все, что нужно знать о таком понятии, как БИССЕКТРИСА. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (3)
«Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.
Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.»
Некорректно, линия бывает разная,а речь здесь идет о прямой, или её порождениях: отрезок и луч.
Математика требует точности. Спасибо.
При ознакомлении с таким теоретическим материалом всегда возникает вопрос, как можно использовать знания о биссектрисе в реальной жизни, за пределами учебного заведения.
Необходимость делать уроки с собственным ребенком в счет не идет. Конечно, такая информация повышает общую эрудицию, но не несет никакой практической нагрузки, а потому надолго не задерживается в памяти.
Никогда не был силен в геометрии, но наука эта очень важна, знаю, потому как не раз приходилось подтягивать свои знания для решения практических задач.