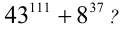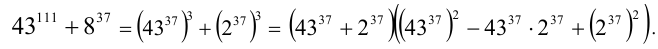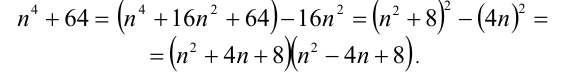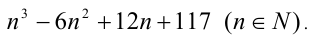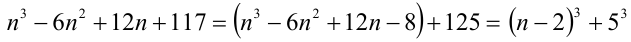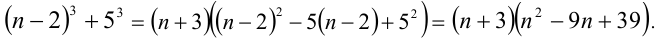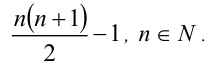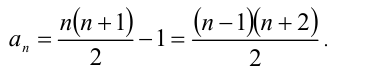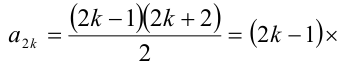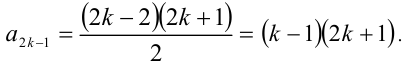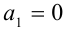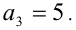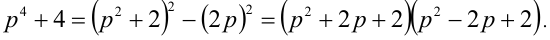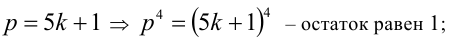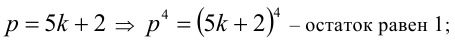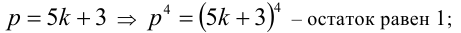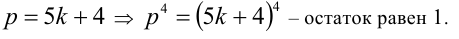Как доказать что число составное

Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена.

В этой статье мы изучим простые и составные числа. Сначала дадим определения простых и составных чисел, а также приведем примеры. После этого докажем, что простых чисел бесконечно много. Далее запишем таблицу простых чисел, и рассмотрим методы составления таблицы простых чисел, особо тщательно остановимся на способе, получившем название решето Эратосфена. В заключение осветим основные моменты, которые нужно учитывать при доказательстве того, что данное число является простым или составным.

Навигация по странице.

Простые и составные числа – определения и примеры

Понятия простые числа и составные числа относятся к целым положительным числам, которые больше единицы. Такие целые числа, в зависимости от количества их положительных делителей, подразделяются на простые и составные числа. Таким образом, чтобы понять определения простых и составных чисел, нужно хорошо представлять себе, что такое делители и кратные.

Составные числа – это целые числа, большие единицы, которое имеют, по крайней мере, три положительных делителя.

Учитывая, что целые положительные числа – это натуральные числа, и что единица имеет только один положительный делитель, можно привести другие формулировки озвученных определений простых и составных чисел.

Простыми числами называют натуральные числа, которые имеют только два положительных делителя.

Составными числами называют натуральные числа, имеющие более двух положительных делителей.

Исходя из информации предыдущего абзаца, можно дать следующее определение составных чисел.

Натуральные числа, которые не являются простыми, называются составными.

Приведем примеры простых и составных чисел.

В заключение этого пункта хочется еще обратить внимание на то, что простые числа и взаимно простые числа – это далеко ни одно и то же.

Таблица простых чисел

Теперь разберемся с возможностью (а точнее с невозможностью) составления таблицы всех существующих простых чисел. Мы не можем составить таблицу всех простых чисел, потому что простых чисел бесконечно много. Последнее утверждение представляет собой теорему, которую мы докажем после следующей вспомогательной теоремы.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Теперь мы можем доказать, что простых чисел бесконечно много.

Простых чисел бесконечно много.

Так доказано, что всегда может быть найдено новое простое число, не заключающееся среди любого количества наперед заданных простых чисел. Следовательно, простых чисел бесконечно много.

Решето Эратосфена

Опишем несколько первых шагов.

Такой подход к составлению таблицы простых чисел является далеко не идеальным. Так или иначе, он имеет право на существование. Отметим, что при этом способе построения таблицы целых чисел можно использовать признаки делимости, которые немного ускорят процесс поиска делителей.

Существует более удобный способ для составления таблицы простых чисел, называемый решето Эратосфена. Присутствующее в названии слово «решето» не случайно, так как действия этого метода помогают как бы «просеять» сквозь решето Эратосфена целые числа, большие единицы, чтобы отделить простые от составных.

Первое записанное число 2 является простым. Теперь от числа 2 последовательно перемещаемся вправо на два числа и зачеркиваем эти числа, пока не доберемся до конца составляемой таблицы чисел. Так будут вычеркнуты все числа, кратные двум.

Давайте еще сформулируем и докажем теорему, которая позволит ускорить процесс составления таблицы простых чисел при помощи решета Эратосфена.

Что же нам дает доказанная теорема, касательно решета Эратосфена?

Данное число простое или составное?

Некоторые задания требуют выяснения, является ли данное число простым или составным. В общем случае эта задача далеко не проста, особенно для чисел, запись которых состоит из значительного количества знаков. В большинстве случаев приходится искать какой-либо специфический способ ее решения. Однако мы попробуем дать направление ходу мыслей для несложных случаев.

Несомненно, можно попробовать воспользоваться признаками делимости для доказательства того, что данное число является составным. Если, к примеру, некоторый признак делимости показывает, что данное число делится на некоторое целое положительное число большее единицы, то исходное число является составным.

Докажите, что число 898 989 898 989 898 989 составное.

Существенный недостаток такого подхода заключается в том, что признаки делимости не позволяют доказать простоту числа. Поэтому при проверке числа на то, является ли оно простым или составным, нужно действовать иначе.

Число 11 723 простое или составное?

Источник

Лекция 8. 22.04.20.ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА

Лекция 8. Простые и составные числа. Их свойства

Определение. Натуральное число, большее единицы, называется простым, если оно делится только на себя и на 1 (т. е. имеет ровно два разных делителя). На­туральное число называется составным, если оно имеет более 2 разных делителей.

Например, числа 2, 3, 5, 7, 11 – простые, а число 18 – составное (1, 2, 3, 6, 9, 18 – его делители). Число 1 имеет только один делитель и не является ни простым, ни составным.

Таким образом, множество целых неотрицательных чисел N₀ можно разделить на четыре непересекающихся подмножества:

1) <0>– множество, состоящее из одного элемента, числа 0:;

2) <1>– множество, состоящее из одного элемента, числа 1;

1) Если простое число p делится на натуральное число q ≠ 1, то q совпадает с числом p (q = p).

Доказательство. Действительно, если бы число p делилось на q и не совпа­да­ло с числом q, то оно имело бы три делителя: 1, p, q, что противоречит опре­делению простого числа. Поэтому p = q.

2) Если p и q – разные простые числа, то p не делится на q.

Доказательство. Поскольку p – простое число, то оно делится только на 1 и p. По условию p ≠ q и q – простое число, значит, q ≠ 1. Отсюда следует, что p не делится на q.

3) Всякое натуральное число a>1 имеет хотя бы один простой делитель, причем этот делитель наименьший.

Доказательство. Если число а – простое, то таким делителем числа а является само это число.

Последнее неравенство противоречит условию, что d – наименьший делитель числа а. Значит, допущение о том, что число d – составное, ошибочно.

Таким образом, наименьший делитель натурального числа а – всегда простое число.

Доказательство. Пусть число а – составное и d – его наименьший простой делитель (он существует на основании свойства 3).

Число 381 – составное, поскольку делится на 3 по признаку делимости.

Решето Эратосфена

Эратосфен – древний греческий ученый математик и астроном, который жил в III в. до н. э. Считают, что он первый составил таблицу простых чисел. В древ­ности греки писали палочками на восковых досках. Записав некоторую после­до­вательность натуральных чисел, Эратосфен прокалывал дырку, где стояли состав­ные числа. Составные числа как бы «просеивались», а оставались только простые. Дощечка выглядела подобно решету. Отсюда, возможно, и название метода Эратосфена отсеивать составные числа.

Решение. Запишем последовательность натуральных чисел от 2 до 40.

Источник

Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена

В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

Простые и составные числа – определения и примеры

Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

Простые числа – это натуральные числа, имеющие только два положительных делителя.

Составное число – это натуральное число, имеющее более двух положительных делителей.

Натуральные числа, которые не являются простыми, называют составными.

Таблица простых чисел

Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

Рассмотрим теорему, которая объясняет последнее утверждение.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Простых чисел бесконечно много.

Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

Решето Эратосфена

Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

Перейдем к формулировке теоремы.

Данное число простое или составное?

Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

Доказать что число 898989898989898989 является составным.

Ответ: 11723 является составным числом.

Источник

math4school.ru

Простые и составные числа

Немного теории

Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.

Приведём некоторые свойства простых чисел.

Основная теорема арифметики. Каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей.

Простых чисел бесконечно много.

Если p – простое, и p делит a·b, то p делит a или b.

Mалая теорема Ферма. Если p – простое, a – натуральное, то a p – a делится на p.

Теорема Вильсона. Натуральное p > 1 является простым тогда и только тогда, когда (p – 1)! + 1 делится на p.

Постулат Бертрана. Если n > 1 – натуральное, то существует простое p, такое, что n 1 – целые взаимно простые числа, содержит бесконечно много простых чисел.

Теорема Ферма. Каждое простое число вида 4k + 1 есть сумма двух квадратов натуральных чисел.

Всякое простое число, большее 3, представимо в виде 6k + 1 или 6k – 1, где k – некоторое натуральное число.

Число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, большим 2.

Число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, большим 1.

Задачи с решениями

1. Три простых числа, каждое из которых больше 10, образуют арифметическую прогрессию. Докажите, что разность прогрессии делится на 6.

Все данные простые числа нечётные, поэтому их разность делится на 2. Покажем, что она делится и на 3. Пусть данные числа a, a + d, a + 2d. Ни одно из них не делится на 3, поэтому при делении на 3 даёт остаток или 1, или 2. Следовательно, по крайней мере, два из этих чисел дают при делении на 3 одинаковые остатки. Разность этих чисел, равная d или 2d, делится на 3. Поскольку 2 на 3 не делится, то d делится на 3. Итак, разность прогрессии, которая делится на взаимно простые числа 2 и 3, делится на 6, что и требовалось доказать.

2. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

3. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

|n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом. Этому требованию удовлетворяют n = 3 и n = 4.

4. Докажите, что если числа

а) m и m 2 + 2 простые, то число m 3 + 2 тоже простое;

б) р, р – 10, р + 10 простые, то число р – 2 тоже простое.

а) Любое простое число m, отличное от 3, можно представить в виде 3n+1 или в виде 3n–1, где n – некоторое натуральное число. В первом случае можно записать

m 2 + 2 = 9n 2 + 6n +3,

m 2 + 2 = 9n 2 – 6n +3,

Так как m > 2, то в любом случае число m 2 +2 больше 3 и делится на 3, а значит является составным. Следовательно, число m 2 +2 может быть простым, только если m = 3. В этом случае m 2 +2 = 11 – простое число, m 3 +2 = 29 – тоже простое число, что и требовалось доказать.

б) Так как р – 10 = (р – 1) – 9 и р + 10 = (р + 1) + 9, то числа р – 10 и р – 1 при делении на 3 имеют одинаковые остатки, и числа р + 10 и р + 1 при делении на 3 имеют одинаковые остатки.

Из трёх последовательных чисел р – 1, р, р + 1 одно и только одно делится на 3. С учётом выше сказанного, то же утверждение верно для чисел р – 10, р, р + 10. Так как эти числа простые, то р – 10 = 3 и р = 13, поэтому р – 2 = 11 – простое число, что и требовалось доказать.

5. Сколько раз входит двойка в разложение на простые множители произведения

Ответ на поставленный вопрос получим из следующих преобразований:

6. Найдите все простые p такие, что число p 2 + 11 имеет ровно 6 различных делителей (включая единицу и само число).

Если p > 5 и простое, то числа p – 1 и p + 1 оба четные, и одно из них кратно трем. Поэтому произведение (p – 1)(p + 1) делится на 12, следовательно, p 2 + 11 также делится на 12, а значит, имеет не менее семи делителей (6 делителей числа 12 и само число p 2 + 11 > 12 ). Осталось проверить p = 2 и p = 3.

Если p = 2, то p 2 + 11 = 2 2 + 11 = 15 имеет 4 делителя (1, 3, 5, 15).

Если p = 3, то p 2 + 11 = 3 2 + 11 = 20 имеет 6 делителей (1, 2, 4, 5, 10, 20).

7. Найти все натуральные числа n, для которых каждое из шести чисел

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

Рассмотрим варианты. Для n = 1 число n + 3 = 4 составное.

Для n = 2 число n + 7 = 9 составное.

Для n = 3 число n + 1 = 4 составное.

Для n > 4 все наши числа больше 5 и по крайней мере одно из них делится на 5, так как числа 1, 3, 7, 9, 13 и 15 при делении на 5 дают соответственно остатки 1, 3, 2, 4, 3 и 0, то есть все возможные остатки, откуда следует, что и числа

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

при делении на 5 дают все возможные остатки и, следовательно, хотя бы одно из них делится на 5 и как число, большее пяти (так как n > 4), является составным.

Но для n = 4 мы получаем простые числа 5, 7, 11, 13, 17 и 19.

8. Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

9. Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

10. Доказать, что для любого простого числа p > 5 уравнение х 4 + 4 x = p в целых числах не имеет решений.

Докажем, что если для некоторого целого значения х число

является целым, то это число либо не превосходит пяти, либо является составным.

Действительно, если х 4 + 4 0 4 + 4 1 = 5.

Если x = 2k (k – натуральное число), то число

f(x) = 2 4 k 4 + 4 2k = 2 4 ( k 4 + 4 2(k–1) )

Наконец, если x = 2k + 1 (k – натуральное число), то число

f(x) = x 4 + 4·4 2k = (x 4 + 4x 2 (2 k ) 2 + 4(2 k ) 4 ) – 4x 2 (2 k ) 2 =

= (x 2 + 2(2 k ) 2 ) 2 – (2·x·2 k ) 2 =

= (x 2 + 2·x·2 k + 2(2 k ) 2 )·( x 2 – 2·x·2 k + 2(2 k ) 2 ) =

= ((x + 2 k ) 2 + 2 2k )·((x – 2 k ) 2 + 2 2k )

так же является составным, поскольку каждый из двух сомножителей последнего произведения больше 1 (ибо 2 2k > 1 при k > 0).

Таким образом, если число p > 5 простое, то равенство х 4 + 4 x = p не выполняется ни при каких целых значениях х.

Задачи без решений

1. Известно, что р, р + 10, р + 14 – простые числа. Найдите число р.

2. Докажите, что число

3. Найдите все простые р для которых число р 2 + 14 так же будет простым числом.

4. Докажите, что уравнение х 2 + х + 1 = р·у имеет решение в целых числах (х, у) для бесконечного числа простых р.

5. Введём обозначение для суммы первых n простых чисел через S_n:

Докажите, что между числами S_n и S_n+1 всегда существует число, являющееся полным квадратом.

Источник

Задачи на простые и составные числа

Задачи на простые и составные числа

Если необходимо выяснить, является ли заданное число простым, то используемый при этом подход основан на попытке разложения исследуемого числа на простые множители, нахождение его делителей, отличных по модулю от единицы и самого числа.

Пример №34.

Доказать, что число р = 389 — простое.

2, 3, 5, 7, 11, 13, 17, 19.

Пример №35.

Является ли простым число

Решение:

Заметим, что данное число есть сумма кубов двух чисел, и разложим его на множители по соответствующей формуле:

Поскольку число удалось разложить на произведение двух натуральных сомножителей, каждый из которых, очевидно, отличен от единицы, то это означает, по определению составного числа, что исходное число было составным.

Пример №36.

Установить, является ли число 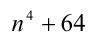простым или составным.

Решение:

Очевидно, достаточно ограничиться рассмотрением случая натуральных n (при целых отрицательных п результат будет аналогичен, а при n = 0 число будет составным). Чтобы дать ответ на этот вопрос, попробуем разложить данное число на множители:

Заметим, что 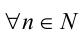каждый из двух сомножителей строго больше единицы (докажите это). Это означает, что исходное число — составное.

Пример №37.

Установить, является простым или составным число

Решение:

Преобразуем данное выражение, выделив в нём полный куб разности

Теперь разложим на множители по формуле суммы кубов:

Очевидно, что при натуральных n оба сомножителя в этом произведении цело-численны и больше единицы. Это означает, что исследуемое число является составным.

Пример №38.

Доказать, что квадрат любого простого числа р > 3 при делении на 12 даёт в остатке 1.

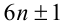
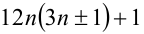
Доказательство. Воспользуемся известным свойством, что любое простое число, большее 3, можно представить в виде . Тогда его квадрат равен , откуда и вытекает требуемое утверждение.

Пример №39.

Пусть р > 5 — простое число. Доказать, что 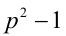делится нацело на 24.

Доказательство.

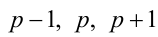
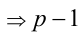
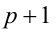
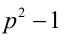
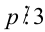
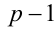
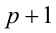
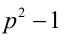
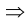
Рассмотрим на числовой прямой три последовательных целых числа . Так как р — простое число, то р нечётно и — чётные последовательные числа, следовательно, одно из них делится на 2, а другое — на 4, но тогда их произведение делится на 8. Далее, поскольку , то либо , либо делится на 3, а значит, их произведение кратно 3. Итак, число делится одновременно на 8 и на 3 делится на 24.

Пример №40.

Найти все простые числа вида

Решение:

Обозначим

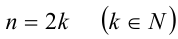
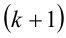
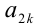
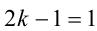
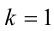
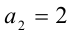
1) Если , то . При натуральных k оба сомножителя натуральны, причём второй сомножитель больше 1, поэтому может быть простым числом, только если т.е. при , тогда .

2) Если 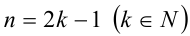, то имеем

При k = 1 имеем

, =0 — не является ни простым, ни составным числом. При k > 2 оба сомножителя целочислснны и больше 1 и, значит, число будет составным. Только при k = 2 получаем простое число

Ответ: таких чисел два: 2 и 5.

Пример №41.

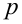
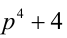
Доказать, что для всех простых чисел число — составное.

Решение:

1-й способ. Разложим исследуемое число на множители:

Так как при простых 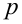оба сомножителя больше единицы (убедитесь в этом самостоятельно), то тем самым необходимое утверждение доказано.

2-й способ. Покажем, что если 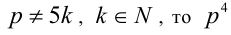при делении на 5 даёт остаток 1:

1)

2)

3)

4)

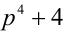
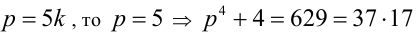
Тогда число делится нацело на 5, а значит, является составным. Если же — составное.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник