Как доказать что фигура параллелограмм по векторам
Как доказать, что фигура – параллелограмм? Какие его признаки?
Содержание:
Параллелограммом – 4-угольник, где противоположные стороны попарно параллельные, одинаковые по длине, а диагонали в точке пересечения делятся на равные отрезки. Изучим признаки параллелограмма по двум, четырём сторонам, внутренним углам, центру симметрии.
Что такое параллелограмм, свойства фигуры
Особенность высоты геометрической фигуры – отрезка, опущенного из любой точки многоугольника на противоположную ей сторону: отсекает от фигуры равнобедренный треугольник.
Свойства биссектрис – отрезков, делящих углы пополам:
У 4-угольника противоположные углы равны, а сумма прилегающих к одному отрезку составляет 180°.
Как доказать, что фигура параллелограмм
Признаки
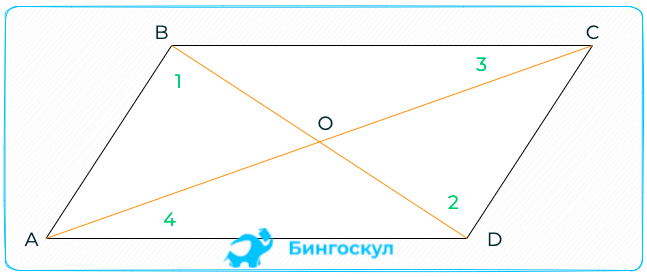
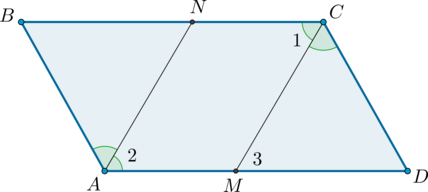
Дан 4-угольник, где AB=CD, BC=AD. Доказать, что AB∥CD, BC∥AD.
Проведём диагональ BD. В итоге получим пару одинаковых треугольников, исходя из условий задачи и общего отрезка BD.
Отсюда вытекают равенства: ∠1 = ∠4, ∠2 = ∠3 – подобные треугольники имеют одинаковые по величине углы, образованные подобными сторонами. Значит AB∥CD и BC∥AD (из свойства: если накрест расположенные углы равны, значит прямые будут параллельными).
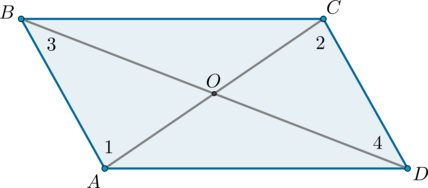
В данном четырёхугольнике BC=AD, BC∥AD. Нужно доказать параллельность AB и CD для подтверждения, что это параллелограмм.
Исходя из условий, понимаем, что BCD и ABD – подобные треугольники. Из условия задачи: BC = AD, BD – общая для обоих, значит, ∠2 = ∠3 – следствие того, что накрест лежащие углы подобные. Из равенства 3-угольников: ∠1 = ∠4 получается, что AB параллельна CD.
Признаки параллелограмма по диагоналям с доказательством
Четырёхугольник обладает и прочими особенностями, рассмотрим одну на примере задачи: докажите признак параллелограмма по точке пересечения диагоналей.
Треугольник AOD равен BOC, потому что AD=BC – лежащие напротив стороны четырёхугольника. ∠1=∠2, ∠3=∠4 – они лежат накрест и параллельных прямых. Если треугольники подобные, значит: OC=OA, OB=OD.
Прочие способы как доказать параллелограмм
Получается, треугольник OAF равен OCE, потому что у них стороны AO = OC. Углы, расположенные у общей вершины O, также равны, ведь они вертикальные. ∠1=∠2 – следствие равности накрест лежащих при параллельных прямых углов. Как результат: OF=OE.
Если у четырёхугольника есть точка, которая обладает описанным свойством, её называют центром симметрии этой геометрической фигуры. Для рассматриваемого многоугольника центром симметрии является точка O, разделяющая диагонали на подобные отрезки.
При повороте геометрической фигуры вокруг центра симметрии на 180° она будет совмещена с предыдущим местоположением, ведь противоположные точки поменяются местами относительно оси симметрии.
Для проверки качества усвоения материала самостоятельно сформулируйте признаки параллелограмма без доказательств.
Доказательство основных свойств параллелограмма при помощи векторно-координатного метода
Дата публикации: 25.03.2021 2021-03-25
Статья просмотрена: 144 раза
Библиографическое описание:
Карымов, И. А. Доказательство основных свойств параллелограмма при помощи векторно-координатного метода / И. А. Карымов. — Текст : непосредственный // Молодой ученый. — 2021. — № 13 (355). — С. 1-8. — URL: https://moluch.ru/archive/355/79495/ (дата обращения: 13.12.2021).
Векторно-координатный метод решения задач является одним из самых мощных способов, использование которого позволяет решать многие физические, технические и математические задачи. Привлекательность данного метода обусловлена его алгоритмичностью — возможностью построения систем последовательных операций, описывающих порядок действий для решения той или иной задачи. В данной статье доказываются основные свойства параллелограмма векторно-координатным методом.
Ключевые слова: векторно-координатный метод, геометрическая задача, свойства параллелограмма.
Данное обстоятельство, сопровождающееся нехваткой времени, необходимого для решения той или иной задачи, вызывают трудности, провоцирующие нас к поиску наиболее оптимального метода решения геометрических задач и его использовании на технологическом уровне.
Векторно-координатный метод используется в различных областях науки и техники, общественной жизни. Данный метод лежит в основе механики, геодезии, экономики, астрономии, географии, медицине. Особая его роль отводится в математике, в частности, при решении геометрических задач. Так данный метод позволяет сопоставить геометрическим объектам (фигурам, отрезкам, векторам), соответствующие им алгебраические соотношения, в результате чего появляются возможности более рационально решать многие задачи, строить доказательства [4].
В данной статье приводятся доказательства основных свойств параллелограмма при помощи векторно-координатного метода.
Основная часть
Для обеспечения овладением первичными навыками использования векторно-координатного метода на практическом уровне рассмотрим основные свойства параллелограмма, установим их истинность при помощи данного метода. Анализ учебников геометрии (Атанасян Л. С. [1], Погорелов А. В. [3], Смирнова, И.М. [5], Шарыгин И.Ф [6]) позволил синтезировать основные свойства параллелограмма.
Свойство 1. Противоположные стороны параллелограмма равны.
Как доказать, что четырехугольник — параллелограмм
Как доказать, что четырехугольник — параллелограмм? Для этого можно использовать определение либо один из признаков параллелограмма.
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.
ABCD — параллелограмм, если
Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.
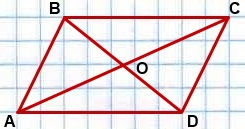
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).
Для этого можно доказать равенство одной из тех же пар треугольников.
Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.
Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.
Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.
Параллелограмм
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Итак, в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник \(ABCD\) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
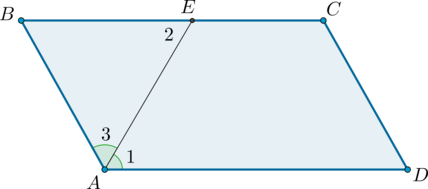
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
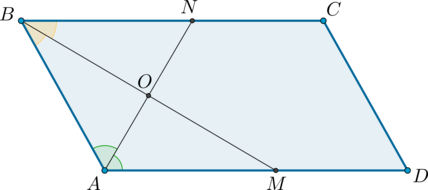
2) Пусть \(ABCD\) – параллелограмм, \(AN\) и \(BM\) – биссектрисы углов \(BAD\) и \(ABC\) соответственно.
Признаки параллелограмма
Признаки параллелограмма — это признаки,
с помощью которых можно доказать,
что четырехугольник — параллелограмм.
Чтобы доказать, что четырехугольник — параллелограмм, нужно знать признаки
параллелограмма. Четырехугольник является параллелограммом, если один
из признаков параллелограмма для этого четырехугольника истинен.
Например, если у четырехугольника две стороны равны и
параллельны, значит этот четырехугольник параллелограмм.
Всего существует три признака параллелограмма: по двум одинаковым
параллельным сторонам, по пересечению диагоналей и делению
диагоналей пополам в точке пересечения, по попарно равным
противоположным сторонам. В этой статье мы рассмотрим
все три признака параллелограмма.
I признак параллелограмма
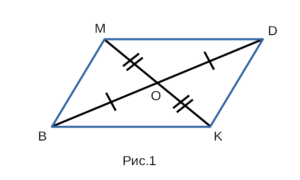
По пересечению диагоналей и делению
диагоналей в точке пересечения пополам.
Четырехугольник является параллелограммом, если у четырехугольника
диагонали пересекаются, и в точке пересечения делятся пополам.
Если на рисунке 1 — BO = OD, MO = OK, то BMDK — параллелограмм.
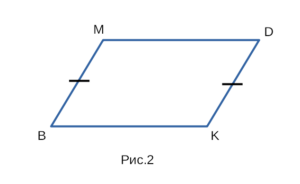
II признак параллелограмма
По двум одинаковым параллельным сторонам.
Четырехугольник является параллелограммом, если у четырехугольника
две стороны равны и параллельны.
Если на рисунке 2 — BM = DK, BM || DK, то BMDK — параллелограмм.
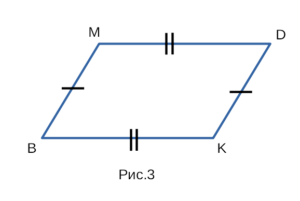
III признак параллелограмма
По попарно равным противоположным сторонам.
Четырехугольник является параллелограммом, если у
четырехугольника противоположные стороны попарно равны.
Если на рисунке 3 — BM = DK, MD = BK, то BMDK — параллелограмм.
В этой статье мы рассмотрели все три признака параллелограмма и
теперь можем доказать, что некий четырехугольник параллелограмм.
В следующей статье про площадь параллелограмма вы узнакете как её расчитать.