Как доказать что функция линейная
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
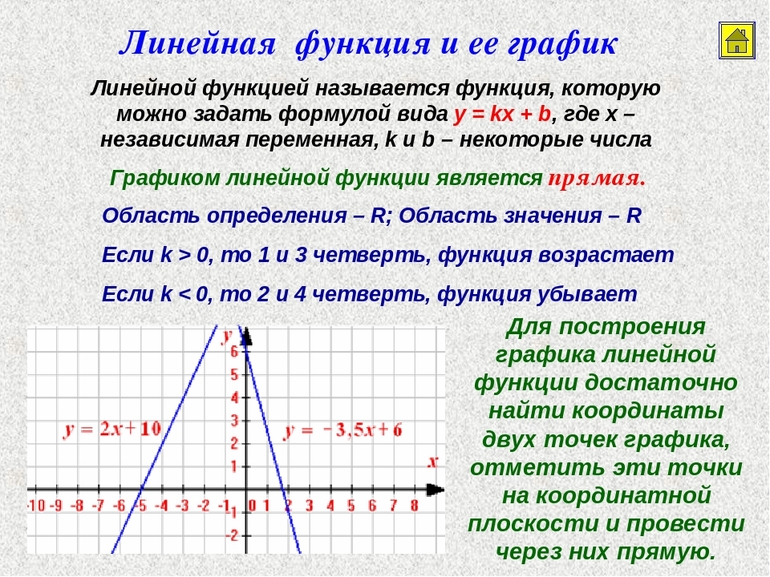
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
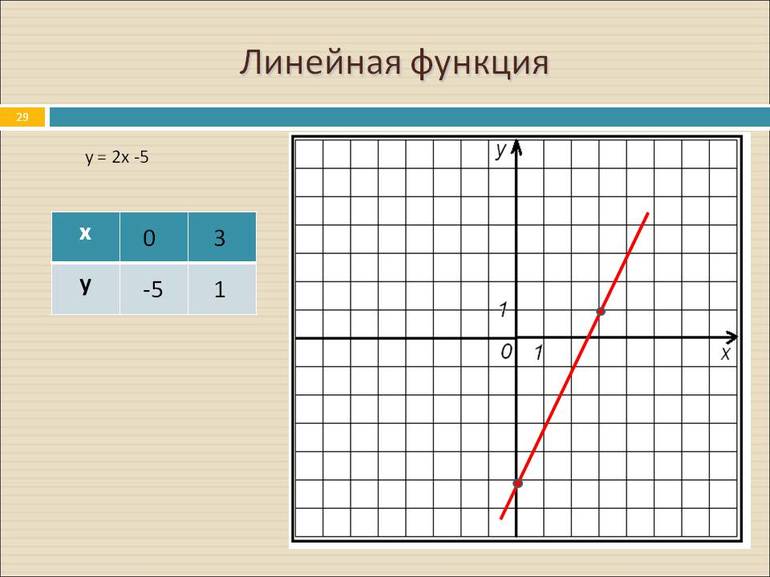
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
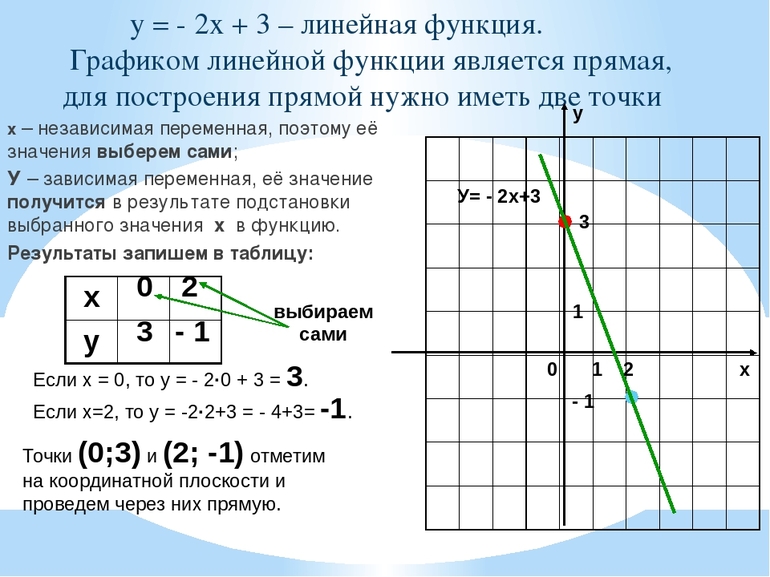
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Линейная функция (ЕГЭ 2022)
Зависимость одной величины от другой математики называют функций одной величины от другой.
Количество денег — это функция вашей зарплаты (иногда говорят «от зарплаты»).
Вес — это функция от съеденных круассанов. Чем меньше съел, тем меньше весишь.
Расстояние — это функция времени. Чем дольше ты будешь идти, тем больше пройдешь.
Ну а теперь перейдем к одному из видов функций – линейной функции.
Линейная функция — коротко о главном
Линейная функция –это функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (коэффициенты).
Рассмотрим, как коэффициенты влияют на месторасположение графика:
Общие варианты представлены на рисунке:
Линейная функция
Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»?
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.
Например, для функции \( y=\sqrt
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
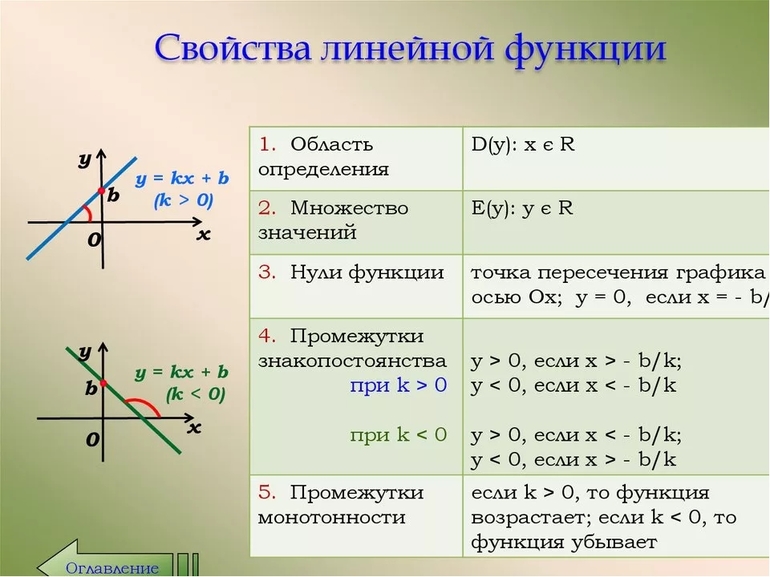
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений \( E\left( y \right)\).
Область определения линейной функции
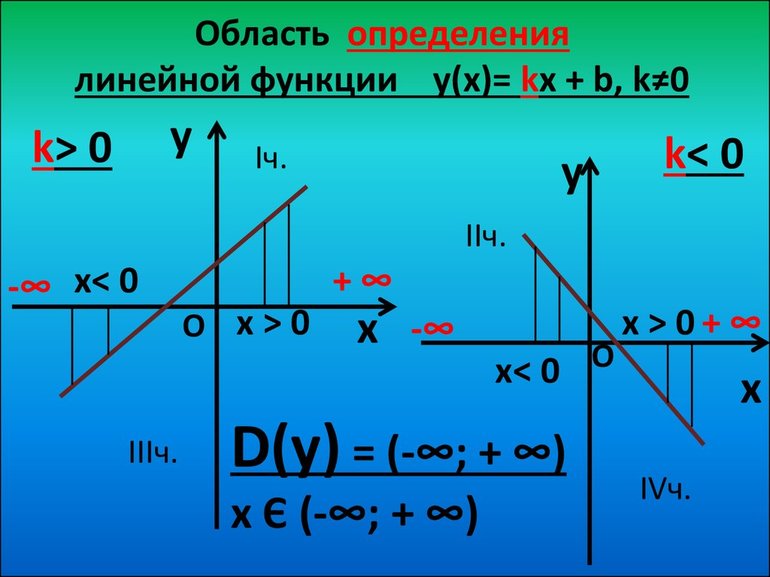
Какими могут быть значения аргумента линейной функции \( y=kx+b\)? Правильно, любыми. Это значит, что область определения – все действительные числа:
\( D\left( y \right)=\mathbb
А множество значений?
Область значений линейной функции
Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент \( x\), тем больше значение функции \( y\).
Значит, \( y\) так же как и \( x\) может принимать все возможные значения, то есть \( E\left( y \right)=\mathbb
Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?
Вспомним формулу: \( y=kx+b\). Какие нужно выбрать коэффициенты \( k\) и \( b\), чтобы значение функции y не зависело от аргумента \( x\)?
А вот какие: \( b\) – любое, но \( k=0\). И правда, каким бы ни был аргумент \( x\), при умножении на \( k=0\) получится \( 0\)!
Тогда функция станет равна \( y=0\cdot x+b=b\), то есть она принимает одно и то же значение при всех \( x\):
\( y = kx + b:<\rm< >>\left[ \begin
Теперь рассмотрим несколько задач на линейную функцию.
Три задачи на линейную функцию
Решение задачи №1
Пусть начальное значение аргумента равно некому числу \( <
Чему была равна функция до увеличения? Подставляем аргумент в формулу:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Решение задачи №2
Аналогично предыдущей задаче:
Начальное значение аргумента равно \( <
Начальное значение функции: \( <
В этот раз функция не увеличилась, а уменьшилась. Это значит, что конечное значение будет меньше начального, а значит, изменение (разность конечного и начального) будет отрицательным:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Определение прямой пропорциональной зависимости
Если проанализировать решения этих двух задач, можно прийти к важному выводу.
При изменении аргумента линейной функции на \( \Delta x\) функция изменяется на \( k\cdot \Delta x\). То есть изменение функции всегда ровно в \( \mathbf
\) раз больше изменения аргумента.
По сути это является определением прямой пропорциональной зависимости.
Решение задачи №3
Подставим известные значения аргумента и функции в формулу \( y=kx+b\):
Получили два уравнения относительно \( k\) и \( b\). Теперь достаточно решить систему этих двух уравнений:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
График линейной функции
Как я уже упоминал ранее, график такой функции – прямая линия.
Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).
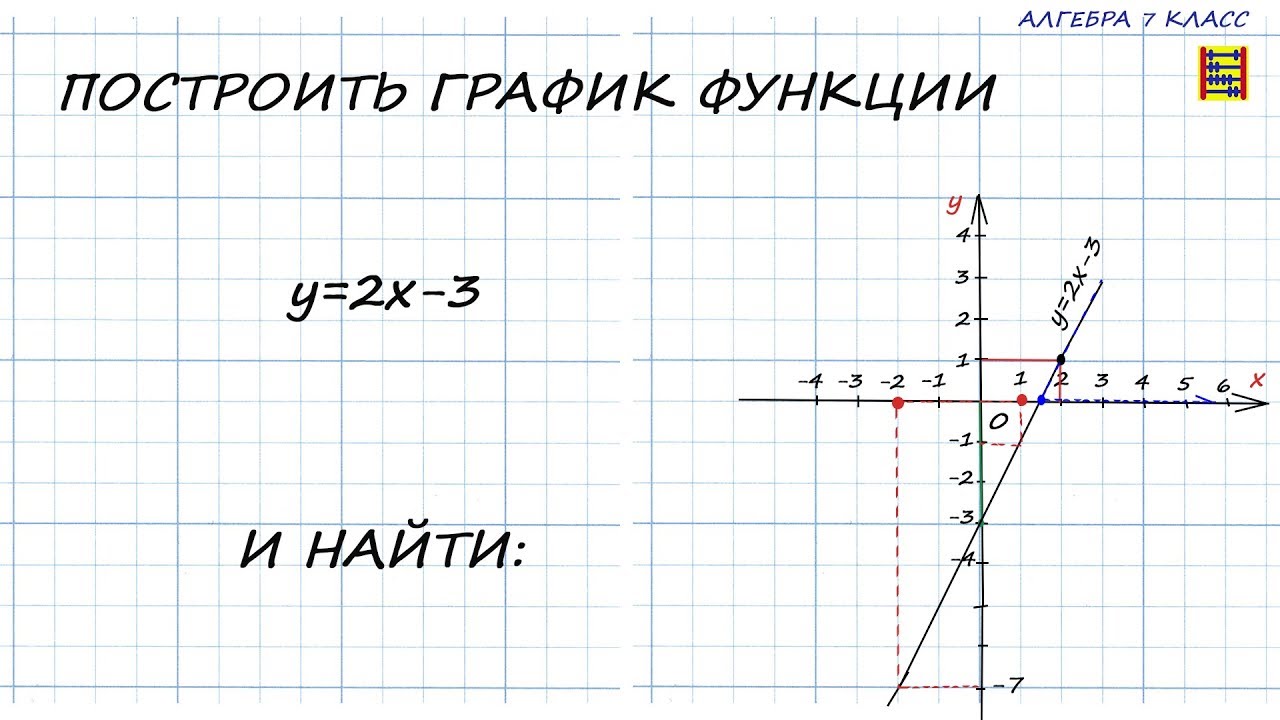
Предположим, у нас есть функция линейная функция \( y=2x+1\). Чтобы построить ее график, нужно вычислить координаты любых двух точек.
То есть нужно взять любые два значения аргумента \( x\) и вычислить соответствующие два значения функции.
Затем для каждой пары \( \left( x;y \right)\) найдем точку в системе координат, и проведем прямую через эти две точки.
Проще всего найти функцию, если аргумент \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Ставим эти две точки на координатной плоскости:
Теперь прикладываем линейку, и проводим прямую через эти две точки:
Вот и все, график построен!
Давай теперь на этом же рисунке построим еще два графика: \( y=
Построй их самостоятельно так же: посчитай значение y для любых двух значений \( x\), отметь эти точки на рисунке и проведи через них прямую.
Должно получиться так:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Видно, что все три прямые по-разному наклонены и в разных точках пересекают координатные оси. Все дело тут в коэффициентах \( \displaystyle k\) и \( \displaystyle b\).
Давай разберемся, на что они влияют.
Коэффициенты линейной функции
Для начала выясним, что делает коэффициент \( \displaystyle b\). Рассмотрим функцию \( \displaystyle y=x+b\), то есть \( \displaystyle k=1\).
Меняя \( \displaystyle b\) будем следить, что происходит с графиком.
Что ты можешь сказать о них? Чем отличаются графики?
Это сразу видно: чем больше \( \displaystyle b\), тем выше располагается прямая.
Более того, заметь такую вещь: график пересекает ось \( \displaystyle \mathbf
И правда. Как найти точку пересечения графика с осью \( \displaystyle y\)? Чему равен \( \displaystyle x\) в такой точке?
В любой точке оси ординат (это название оси \( \displaystyle y\), если ты забыл) \( \displaystyle x=0\).
Значит достаточно подставить \( \displaystyle x=0\) в функцию, и получим ординату пересечения графика с осью \( \displaystyle y\):
\( \displaystyle y=k\cdot 0+b=b\)
Теперь по поводу \( \displaystyle k\). Рассмотрим функцию \( \displaystyle \left( b=0 \right).\) Будем менять \( \displaystyle k\) и смотреть, что происходит с графиком.
Так, теперь ясно: \( \displaystyle k\) влияет на наклон графика.
Чем больше \( \displaystyle k\) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – \( \displaystyle Ox\)) расположена прямая.
Если \( \displaystyle k>0\), график наклонен «вправо», при \( \displaystyle k
Выберем на графике две точки \( \displaystyle A\) и \( \displaystyle B\). Для простоты выберем точку \( \displaystyle A\) на пересечении графика с осью ординат. Точка \( \displaystyle B\) – в произвольном месте прямой, пусть ее координаты равны \( \displaystyle \left( x;y \right)\).
Рассмотрим прямоугольный треугольник \( \displaystyle ABC\), построенный на отрезке \( \displaystyle AB\) как на гипотенузе.
Из рисунка видно, что \( \displaystyle AC=x\), \( \displaystyle BC=y-b\).
Подставим \( \displaystyle y=kx+b\) в \( \displaystyle BC:BC=y-b=kx+b-b=kx\).
Получается, что \( BC = k \cdot AC<\rm< >> \Rightarrow <\rm< >>k = \frac<
Итак, коэффициент \( \displaystyle k\) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.
Именно поэтому его (коэффициент \( \displaystyle k\)) обычно называют угловым коэффициентом.
В случае, когда \( k
Если же \( \displaystyle k=0\), тогда и \( <\mathop<\rm tg>\nolimits> \alpha = 0,\) следовательно \( \displaystyle \alpha =0\), то есть прямая параллельна оси абсцисс.
Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.
Разбор еще трех задач на линейную функцию
1. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
2. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
3. График какой из функций изображен на рисунке?
Решение задачи №1
Коэффициент \( b\) найти проще простого – это ведь точка пересечения графика с осью \( \displaystyle Oy\):
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\):
Общие сведения
В математике существует определение линейной функции, которое частично ее характеризует. Однако этого недостаточно для построения графика и дальнейшего исследования. На основании определений формулируются теоремы. Последние необходимо доказывать, а полученный результат применять для решения различных задач.
Функцией называется зависимость одной величины от другой, которая может быть выражена простым или сложным законом. Зависимая величина называется значением функции. Аргументом является любое значение независимой переменной, но при условии, что в результате подстановки она не обращает функцию в неопределенность.
Простым примером может быть выражение z = 1 / p (гипербола). Величина p может принимать любые значения, кроме 0. Примером линейной функции является тождество z = 4 * v. Следует отметить, что v может принимать любые значения. Если v = 0, то на графике следует отметить точку в центре координат (v = 0; z = 4 * 0 = 0).
После небольшого вступления необходимо разобрать прямоугольную систему координат, так как в ней нужно выполнять построение функции линейной зависимости.
Декартова система координат
Для построения графиков функций применяется специальный инструмент. Он называется координатной системой или плоскостью. Пользуется высокой популярностью прямоугольная декартова система координат (рис. 1), состоящая из двух осей. Последние пересекаются под прямым углом. Горизонтальная называется осью абсцисс, а вертикальная — ординат. Значения последней зависят от первой, хотя их можно поменять местами. Чтобы не было путаницы, нужно придерживаться первого варианта.
Рисунок 1. Декартова прямоугольная система координат на плоскости (ДПСКП).
Ось ординат часто обозначают OY, а абсцисс — OX. Точкой их пересечения считается О. Названия осей можно изменить. Кроме того, подобную операцию можно осуществить и с их центром. Например, его можно обозначить G, O’, O1 и т. д. Этот прием используется для решения задач с несколькими системами. Например, одна из них находится в другой, то есть применяется для решения упражнений на повороты и подобия фигур.
Прямоугольная система разделена на четыре четверти. Если функция находится в первой (I), то она является положительной. Координаты также имеют свой знак (положительный или отрицательный). Эту особенность следует учитывать для решения задач. Например, пусть дана абсцисса t и ордината v. Специалисты рекомендуют разобрать свойства четвертей, используя такие обозначения и свойства знаков:
В первом случае угол f является острым, то есть он меньше 90 градусов, а во втором — тупым. Если к = 0, то, выполнив необходимые математические преобразования, можно сделать вывод о том, что он параллелен оси OX. Важным элементом, который применяется для построения графика, считается предварительное исследование искомой функции.

Элементы исследования функции
Исследование функции применяется для анализа (объяснения) ее свойств и построения графика с учетом характерных особенностей. Операцию следует выполнять строго по алгоритму. В некоторых случаях допускается опускать отдельные элементы, которые не нужны по условию задачи. Необходимо выяснить характер поведения функции. Анализируется она по такому перечню: поиск области определения и допустимых значений, нулей и знаковых промежутков, периодичности, монотонности и экстремумов. Также проводится анализ на четность.
Далее строится график с учетом результатов исследования, на основании которых можно построить даже приближенное графическое представление. Перед тем как приступить к исследованию, необходимо разобрать правила записи интервалов в математике. Этот момент является очень важным, поскольку от него зависит правильность построения и анализа функции. Существует такая международная форма их записи:
Нужно разобрать несколько примеров. Промежуток вида [2;5) означает, что в интервал входят следующие числа: 2, 3 и 4. Следует отметить, что бесконечность может быть положительной и отрицательной. В первом случае перед значком не указывается знак +, хотя при желании это можно сделать, поскольку эта форма записи не считается ошибкой. Отрицательная большая величина обозначается -inf, -бесконечность или -∞. Далее следует подробно рассмотреть область определения и понятие о допустимых значениях.

Области определения
Область определения функции — допустимый интервал значений, которые принимает ее аргумент. Иными словами, это значения независимой переменной, при подстановке которых выражение продолжает существовать и не считается неопределенностью. Простой пример: p = 1 / s. Это выражение является неопределенностью только при значении s = 0, поскольку на 0 делить нельзя. Обозначать область определения следует таким образом: D(имя функции). Для функции p = 1 / s запись производится в таком виде: D(p) = (-∞;0) U (0; ∞).
Следующим элементом является область допустимых значений функции (E(p)), которая представляет промежуток значений выражения на заданном интервале. Однако не следует путать эти два термина, поскольку вычисляются они по разным алгоритмам. Если D(p) записывается некоторым промежутком аргумента, то поиск E(p) сводится к определению точек экстремума и дальнейшей проверке их соответствия искомому интервалу.

Нулевые значения и знаковые интервалы
Нулями функции вида у = k * х + b называются все значения зависимой и независимой величин, при которых график пересекается с осями прямоугольной системы координат. Выполняется операция нахождения нулей по таким формулам:
Интервалом знакопостоянства называется совокупность определенных промежутков, на которых функция меняет знак на противоположный. Для этого применяется частичное исследование:
У линейной зависимости нет точек разрыва, поскольку ее геометрической интерпретацией является прямая. Промежутки знакового поведения указываются таким образом:
На ОХ следует обозначать только значения, которые входят в D(z). Все остальные нужно отсеивать, поскольку они являются ложными.
Характер периодичности и четности
Чтобы проверить четность, нужно применить другую формулу: z(p) = z(-p). Для реализации проверки нужно подставить сначала положительное значение аргумента, а затем отрицательное. Далее следует сравнить ответы. Если равенство соблюдается, то можно сделать вывод о четности искомого тождества. Для определения нечетности существует другая формула: -z(p) = z(-p). Однако бывают случаи, когда ни одно из равенств не выполняется. Тогда математики говорят, что искомая функция не является четной и нечетной.
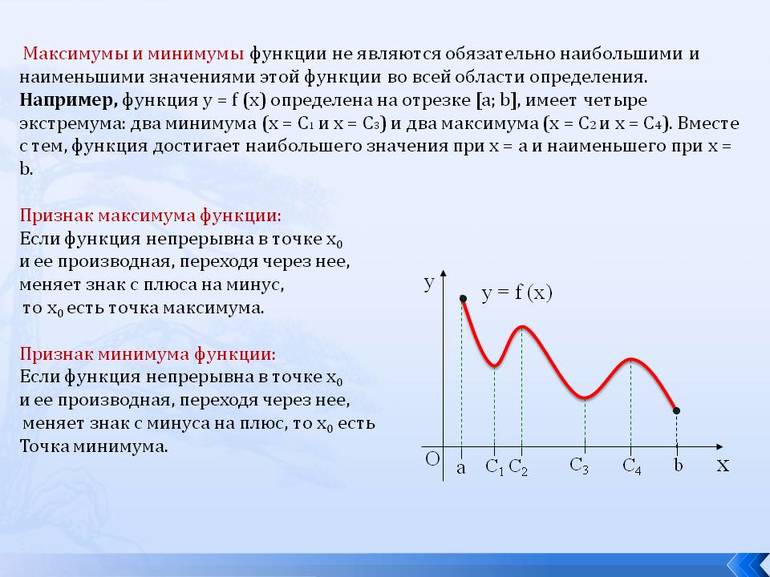
Монотонность, минимум и максимум
Монотонностью функции называется ее способность к возрастанию или убыванию на всей области допустимых значений. Для определения этого параметра существует элементарный алгоритм:
Для поиска минимального и максимального значений (экстремумов) на необходимом промежутке или всей числовой оси нужно применить такую инструкцию:
Математики рекомендуют учитывать каждую точку. Кроме того, необходимо отсеять ложные корни. Для этого следует подставить полученные значения переменной в уравнение, а затем произвести расчеты. Должно быть соответствие левой и правой частей.
Свойства зависимости
Перед тем как решать задачи, нужно обратить внимание на свойства линейной функции. Существуют два положения, которые зависят от коэффициента k. При k > 0 функция обладает такими свойствами: