Как доказать что функция монотонна на всей числовой прямой

Как доказать что функция монотонна на всей числовой прямой

Пусть \(y = f\left( x \right)\) является дифференцируемой функцией на интервале \(\left( \right).\) Функция называется возрастающей (или неубывающей ) на данном интервале, если для любых точек \(, \in \left( \right),\) таких, что \( строго возрастающей на интервале \(\left( \right).\)

Аналогично определяются убывающая (или невозрастающая ) и строго убывающая функции.

Если функция \(f\left( x \right)\) дифференцируема на интервале \(\left( \right)\) и принадлежит к одному из четырех рассмотренных типов (т.е. является возрастающей, строго возрастающей, убывающей или строго убывающей), то такая функция называется монотонной на данном интервале.

Снова рассмотрим функцию \(y = f\left( x \right),\) считая ее дифференцируемой на некотором интервале \(\left( \right).\) Возрастание или убывание функции на интервале определяется по знаку первой производной функции.

Поскольку \(f’\left( c \right) \ge 0,\) то правая часть равенства неотрицательна. Следовательно, \[f\left( <> \right) \ge f\left( <> \right).\] т.е. функция \(y = f\left( x \right)\) является возрастающей на интервале \(\left( \right).\)

Рассмотрим теперь случаи строгого возрастания и строгого убывания функции. Здесь существует похожая теорема, описывающая необходимые и достаточные условия. Опуская доказательство, сформулируем ее для случая строго возрастающей функции.

\(f’\left( x \right) \ge 0\;\forall\;x \in \left( \right);\)

Производная \(f’\left( x \right)\) тождественно не равна нулю ни в каком промежутке \(\left[ <,> \right] \in \left( \right).\)

Условие \(1\) содержится в теореме \(1\) и является признаком неубывающей функции. Дополнительное условие \(2\) требуется для того, чтобы исключить участки постоянства функции, в которых производная функции \(f\left( x \right)\) тождественно равна нулю.

На практике (при нахождении интервалов монотонности) обычно используется достаточное условие строгого возрастания или строгого убывания функции. Из теоремы \(2\) следует такая формулировка достаточного признака:

Соответственно, условие \(f’\left( x \right) строго убывающую функцию.

Число точек, в которых \(f’\left( x \right) = 0,\) является, как правило, конечным. Согласно теореме \(2\), они не могут плотно заполнять какой-либо промежуток в интервале \(\left( \right).\)

Приведем также признак строгого возрастания (убывания) функции в точке:

Если \(f’\left( <> \right) > 0\), то функция \(f\left( x \right)\) строго возрастает в точке \(\);

Если \(f’\left( <> \right) сумма функций \(f + g\) также возрастает (убывает) на этом интервале.

Если функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) то противоположная функция \(-f\) убывает (возрастает) на этом интервале.

Если функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) то обратная функция \(\large\frac<1>\normalsize\) убывает (возрастает) на этом интервале.

Если функции \(f\) и \(g\) возрастают (убывают) на интервале \(\left( \right)\) и, кроме того, \(f \ge 0\), \(g \ge 0\), то произведение функций \(fg\) также возрастает (убывает) на этом интервале.

Если функция \(g\) возрастает (убывает) на интервале \(\left( \right),\) а функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) где \(g:\left( \right) \to \left( \right),\) то композиция функций \(f \circ g\) (т.е. сложная функция \(y = f\left( \right)\) также возрастает (убывает) на интервале \(\left( \right).\)

Данная функция является суммой функций \(\) и \(3.\)

Первую функцию \(\) можно рассматривать как произведение двух одинаковых функций \(\). Из примера \(1\) следует, что квадратичная функция \(\) строго возрастает при \(x \ge 0.\) Следовательно, функция \(\) также строго возрастает при \(x \ge 0\) на основании свойства \(4\).

Второе слагаемое \(3\) представляет собой трехкратную сумму функций \(\) и, поэтому, также является строго возрастающей (на основании свойства \(1\)).

Итак, исходная функция \(f\left( x \right) = + 3\) является суммой двух строго возрастающих функций и, следовательно, также строго возрастает при \(x \ge 0.\)

Для контроля рассмотрим также неравенство \(f’\left( x \right) Рис.5

Следовательно, на основании достаточного признака монотонности, функция строго возрастает при \(x \in \left( <\large\frac<1>\normalsize,\infty > \right)\) и строго убывает при \(x \in \left( <0, \large\frac<1>\normalsize> \right).\) Ее вид схематически приведен на рисунке \(10\).

На основании достаточного признака монотонности заключаем, что функция возрастает при \(x \in \left( <0,\large\frac<1><2>\normalsize> \right)\) и убывает при \(x \in \left( <\large\frac<1><2>\normalsize,1> \right).\) График функции представляет собой полуокружность с центром в точке \(\left( <\large\frac<1><2>\normalsize,0> \right)\) и радиусом \(<\large\frac<1><2>\normalsize>\) (рисунок \(14\)).

Источник

Общие сведения

Функцией вида р = f(r) называется зависимость ее значения от переменной величины «r» или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.

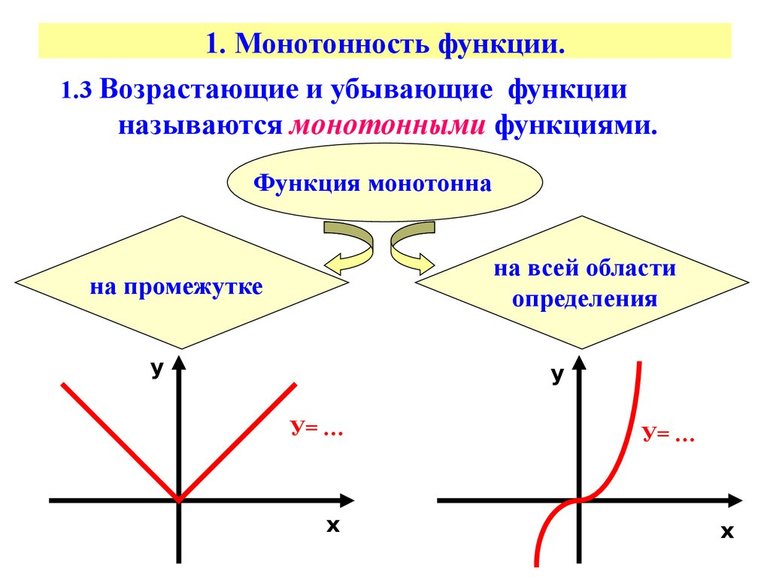
Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) = f(r2) соответственно. Кроме того, нужно учитывать, что r1 =» следует заменить на строгий « »: f(r1) f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:

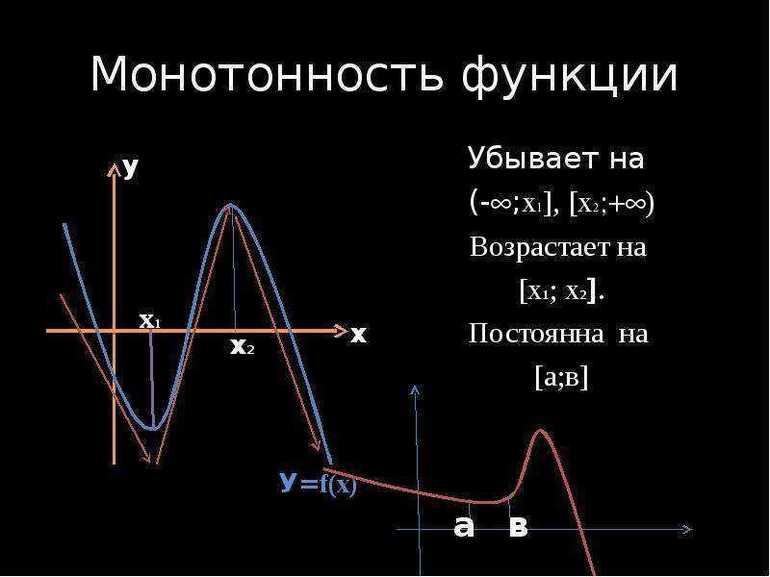
Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.

Теорема о пределе

Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.

Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.

Критерии возрастания и убывания

Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:

Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) = 0 соответственно (при r ∈ данному интервалу).

Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) 0.

Основные свойства

Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:

После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.

Базовые знания

Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:

Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.

Нахождение производной

Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.

Рисунок 1. Дифференциалы простых выражений.

Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:

Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.

Корни уравнений и критические точки

Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.

Источник