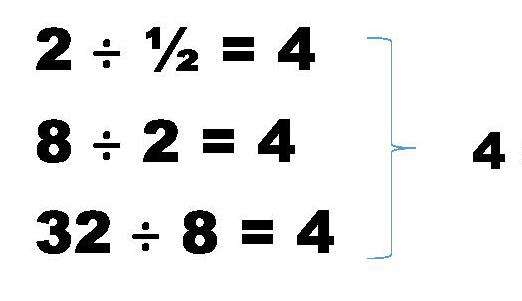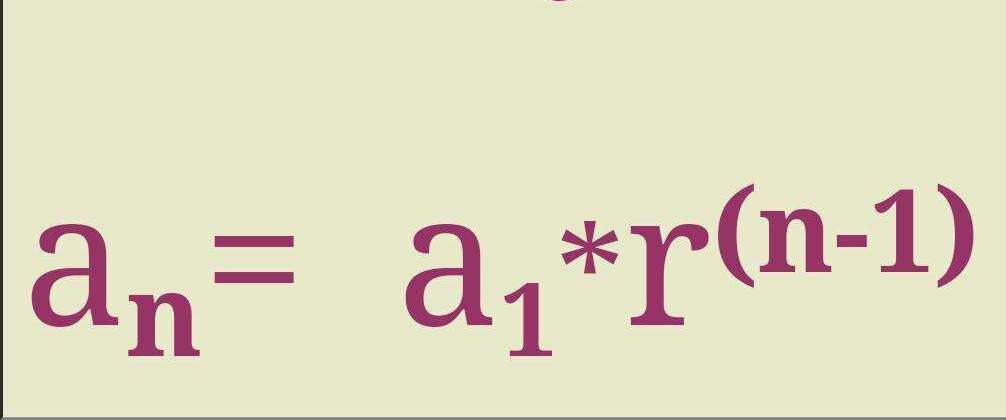Как доказать что геометрическая прогрессия бесконечно убывающая

Бесконечная убывающая геометрическая прогрессия и парадокс Зенона

Когда в общеобразовательных школах изучают свойства упорядоченных последовательностей чисел, то в обязательном порядке рассматривают так называемую убывающую бесконечную геометрическую прогрессию. Раскроем подробнее этот вопрос в статье.

Что такое геометрическая прогрессия?

Вам будет интересно: Future in the Past: правила речи, склонение, время, понятие, определения, особенности изучения и нюансы произношения

Исходя из определения этого вида прогрессии, можно n-й ее член найти, используя следующее выражение: an = a1*r(n-1), то есть достаточно знать знаменатель и первый член числового ряда.

Например, найдем 8-е число в геометрической прогрессии, приведенной выше. Имеем: a8 = a1*r7 = 1*47 = 16384.

Еще одной важной формулой для геометрической прогрессии является выражение для нахождения суммы ее n первых членов. Эта формула имеет вид: Sn = a1*(rn-1)/(r-1). Применим ее для нахождения суммы 8-ми чисел из последовательности выше. Получаем: S8 = 1*(48-1)/(4-1) = 21845.

Какие бывают геометрические прогрессии

В зависимости от знака и модуля знаменателя r выделяют 4 вида геометрической прогрессии:

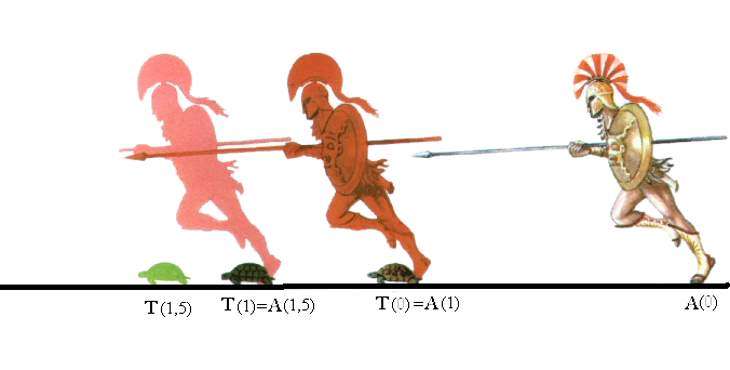
Черепаха и Ахиллес (парадокс Зенона)

Где можно использовать результат, полученный в пункте выше? Например, при объяснении парадокса древнегреческого философа Зенона. Суть этого парадокса заключается в том, что Ахиллес (с древнегреческого языка это имя переводится, как «тот, кто обладает «легкими» ногами»), будучи самым быстрым воином, не может догнать черепаху.

Зенон рассуждал следующим образом: если черепаха будет впереди Ахиллеса, и они одновременно начнут движение, то когда воин достигнет места, откуда взяла старт черепаха, последняя уже отползет на некоторое расстояние, поэтому Ахиллесу придется снова его преодолевать (хотя оно и меньше, чем первоначальное). Пробежав новый отрезок пути, воин все равно окажется позади черепахи, ведь она опять проползет некоторую дистанцию. Так способом можно рассуждать до бесконечности.

Каждый из нас знает, что не только Ахиллес, но и любой человек, двигаясь пешком, обгонит черепаху. В чем же ошибся философ? Он не учел, что хотя сумма отрезков является бесконечной, она приводит к конечному числу S∞. Как только Ахиллес преодолеет расстояние S∞, он сразу же обгонит черепаху.

Любопытно отметить, что сам философ объяснял тот факт, что Ахиллес на практике все же обгоняет черепаху, тем, что движение и время являются иллюзией, и в реальности не существуют.

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Геометрическая прогрессия

Cумма геометрической прогрессии со знаменателем q, b=1 :

$$S=1 + q +q^2+\cdots=1+q(1+q+\cdots) = 1+q\cdot S$$

Эта же техника может быть использована при вычислении любых самоподобных выражений.

Периодические дроби

Обращение бесконечных периодических дробей в обыкновенные дроби:

$0,(7) = 0,7+0,07+0,007+\ldots = 0,7 / (1-0.1) = 7/10 / (9/10) = 7/9$

Геометрическая интерпретация

Сходимость геометрической прогрессии при q=1/2, b=1/2:

Шутка

Легенда о шахматной доске

Шахматы – одна из самых древних игр. Она существует уже многие века, и неудивительно, что с нею связаны различные предания, правдивость которых, за давностью времени, невозможно проверить.

Об одной из подобных легенд и математической составляющей ее содержания мы сегодня и поведём речь. Чтобы понять ее, не нужно вовсе уметь играть в шахматы: достаточно знать, что игра происходит на доске, разграфленной на 64 клетки.

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.

– Я достаточно богат, чтобы исполнить самое смелое твое пожелание, – сказал царь.– Назови награду, которая тебя удовлетворит, и ты получишь ее.

он удивил царя беспримерной скромностью своей просьбы.

– Повелитель, – сказал Сета,– прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

– Простое пшеничное зерно? – изумился царь.

– Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвертую – 8, за пятую – 16, за шестую – 32…

–Довольно, – с раздражением прервал его царь.– Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моею милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.

– Повелитель, – был ответ, – приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.

Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно.

Вечером, отходя ко сну, царь еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.

– Повелитель, – ответили ему,– математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.

– Почему медлят с этим делом? – гневно воскликнул царь. – Завтра, прежде чем я проснусь, все до последнего зерна должно быть выдано Сете. Я дважды не приказываю.

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.

– Прежде чем скажешь о твоем деле, – объявил Шерам,– я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.

– Ради этого я и осмелился явиться перед тобой в столь ранний час,– ответил старик.– Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…

– Как бы велико оно ни было, – надменно перебил царь, житницы мои не оскудеют. Награда обещана и должна быть выдана…

– Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду. С изумлением внимал царь словам старца.

– Назови же мне это чудовищное число, – сказал он в раздумье.

– Восемнадцать квинтиллионов четыреста сорок шесть квадриллионов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!

S = 18 446 744 073 709 551 615.

Это количество зерна примерно в 1800 раз превышает мировой урожай пшеницы за год (в 2008 – 2009 аграрном году урожай составил 686 млн тонн), то есть превышает весь урожай пшеницы, собранный за всю историю человечества.

Индусский царь не в состоянии был выдать подобной награды. Но он легко мог бы, будь он силен в математике, освободиться от столь обременительного долга. Для этого нужно было лишь предложить Сете самому отсчитать себе зерно за зерном всю причитавшуюся ему пшеницу.

В самом деле: если бы Сета, принявшись за счет, вел его непрерывно день и ночь, отсчитывая по зерну в секунду, он в первые сутки отсчитал бы всего 86 400 зерен. Чтобы отсчитать миллион зерен, понадобилось бы не менее 10 суток неустанного счета. Один кубический метр пшеницы он отсчитал бы примерно за полгода. И осталось бы отсчитать ещё 1 499 999 999 999 м3. Вы видите, что, посвятив счету даже весь остаток своей жизни, Сета получил бы лишь ничтожную часть потребованной им награды.

Экспоненциальный рост

Стремительное возрастание значений величины, подобное тому, которое мы наблюдали, в математике называется экспоненциальным ростом.

Экспоненциальный рост – возрастание величины, когда скорость роста пропорциональна значению самой величины. Говорят, что такой рост подчиняется экспоненциальному закону. В случае дискретной области определения с равными интервалами его еще называют геометрическим ростом (значения функции образуют геометрическую прогрессию).

Для любой экспоненциально растущей величины чем большее значение она принимает, тем быстрее растет. Также это означает, что величина зависимой переменной и скорость ее роста прямо пропорциональны.

Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов.

Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейной или степенной зависимостям.

Сумма бесконечной геометрической прогрессии

Геометрическая прогрессия бывает убывающей, если знаменатель по модулю меньше единицы.

Убывающую геометрическую прогрессию можно видеть, например, в апориях Зенона «Деление пополам» и «Ахиллес и черепаха». В первом случае наглядно показывается, что вся дорога (предположим, длины 1) является суммой бесконечного числа отрезков 1/2, 1/4, 1/8 и т. д. Так оно, конечно, и есть с точки зрения представлений о конечной сумме бесконечной геометрической прогрессии. И все же – как такое может быть?

Прогрессия с коэффициентом 1/2

Предел складывания бумаги

Предел складывания бумаги пополам — физический феномен, суть которого состоит в том, что лист обычной бумаги размера А4 можно сложить пополам не более 7 раз. Он происходит из-за быстроты роста показательной функции.

Если бумагу сложили пополам пять раз, то количество слоёв будет два в степени пять, то есть тридцать два.

Если бумагу сложили пополам 7 раз, то количество слоёв будет два в степени 7, то есть 128.

Уже в Древнем Египте знали не только арифметическую, но и геометрическую прогрессию. Вот, например, задача из папируса Райнда: «У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»

Людей всего 7, кошек 72 = 49, они съедают всего 73 = 343 мыши, которые съедают всего 74 = 2401 колосьев, из них вырастает 75 = 16807 мер ячменя, в сумме эти числа дают 19 607.

Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Задача

Источник

Геометрическая прогрессия (ЕГЭ 2022)

Читай эту статью и смотри вебинар по экономической задаче (ЕГЭ №17).

Да, да, экономическая задача — это часто задача на геометрическую прогрессию.

Геометрическая прогрессия — коротко о главном

Геометрическая прогрессия <\( \displaystyle <_>\)> – это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число \( \displaystyle q

0\). Это число называют знаменателем геометрической прогрессии.

Знаменатель геометрической прогрессии может принимать любые значения, кроме \( \displaystyle 0\) и \( \displaystyle 1\).

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и \( \displaystyle n\)-ное число) всегда одно.

Число с номером \( \displaystyle n\) называетмя \( \displaystyle n\)-ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, \( \displaystyle a\)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,\text< ><_<10>>,\text< >…,\text< ><_>\).

Самые распространенные виды прогрессии это арифметическая и геометрическая. В этой теме мы поговорим о втором виде – геометрической прогрессии.

Определение геометрической прогрессии

Допустим, у нас есть числовая последовательность:

Ты сразу же ответишь, что это легко и имя такой последовательности — арифметическая прогрессия с разностью ее членов \( \displaystyle d\text< >=\text< >2\).

А как на счет такой числовой последовательности?

Если ты будешь вычитать из последующего числа предыдущее, то ты увидишь, что каждый раз получается новая разница (\( \displaystyle 9; 90; 900\) и т.д.).

Но последовательность определенно существует и ее несложно заметить – каждое следующие число в \( \displaystyle 10\) раз больше предыдущего!

Такой вид числовой последовательности называется геометрической прогрессией и обозначается \( \displaystyle <_>\).

Геометрическая прогрессия <\( \displaystyle <_>\) > — это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число \( \displaystyle \mathbf\text< >\ne \text< >0\).

Это число называют знаменателем геометрической прогрессии.

Ограничения геометрической прогрессии

Первый член <\( \displaystyle <_<1>>\)> не равен \( \displaystyle 0\) и \( \displaystyle \mathbf\text< >\ne \text< >0\).

Эти ограничения не случайны!

Допустим, что их нет, и первый член прогрессии все же равен \( \displaystyle 0\), а q равно, хм.. пусть \( \displaystyle 2\), тогда получается:

\( \displaystyle <_<1>>=0\cdot 2=0…\) и так далее.

Согласись, что это уже никакая не прогрессия.

Как ты понимаешь, те же самые результаты мы получим, если \( \displaystyle <_<1>>\) будет каким-либо числом, отличным от нуля, а \( \displaystyle q=0\).

В этих случаях прогрессии просто не будет, так как весь числовой ряд будут либо все нули, либо одно число, а все остальные нули.

Теперь поговорим поподробнее о знаменателе геометрической прогрессии, то есть о \( \displaystyle q\).

Знаменатель геометрической прогрессии

Повторим: \( \displaystyle q\) – это число, во сколько раз изменяется каждый последующий член геометрической прогрессии.

Как ты думаешь, каким может быть \( \displaystyle q\)? Правильно, положительным и отрицательным, но не нулем (мы говорили об этом чуть выше).

Допустим, что \( \displaystyle q\) у нас положительное. Пусть в нашем случае \( \displaystyle q=3\), а \( \displaystyle <_<1>>=4\).

Чему равен второй член \( \displaystyle <_<2>>\) и \( \displaystyle <_<3>>\)? Ты без труда ответишь, что:

\( \displaystyle <_<2>>=4\cdot 3=12\) \( \displaystyle <_<3>>=12\cdot 3=36\)

Все верно. Соответственно, если \( \displaystyle q>0\), то все последующие члены прогрессии имеют одинаковый знак – они положительны.

А что если \( \displaystyle q\) отрицательное? Например, \( \displaystyle q=-3\), а \( \displaystyle <_<1>>=4\). Чему равен второй член \( \displaystyle <_<2>>\) и \( \displaystyle <_<3>>\)?

Это уже совсем другая история

Таким образом, если \( \displaystyle q Пример 1. Попробуй определить, какие числовые последовательности являются геометрической прогрессией, а какие арифметической:

Разобрался? Сравним наши ответы:

Как найти любой член геометрической прогрессии

Если в геометрической прогрессии (𝑏_𝑛) вы знаете первый член 𝑏₁ и знаменатель 𝑞, то вы можете найти любой член прогрессии по формуле:

Ну чтобы не считать «врукопашную» (как в примере №2 ниже).

Пример 2. Найти 6-й член прогрессии

Вернемся к нашей последней прогрессии \( \displaystyle q=-3\), а \( \displaystyle <_<1>>=4\) и попробуем так же как и в арифметической найти ее \( \displaystyle 6\) член.

Как ты уже догадываешься, есть два способа его нахождения:

1-й способ. Последовательно умножаем каждый член на \( \displaystyle q\).

2-й способ. По формуле, которая поможет найти тебе любой член геометрической прогрессии.

Если нам нужно найти значение числа прогрессии с порядковым номером, то мы умножаем первый член геометрической прогрессии \( \displaystyle <_<1>>\) на знаменатель \( \displaystyle q\) в степени, которая на \( \displaystyle 1\) единицу меньше, чем порядковый номер искомого числа.

Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

\( \displaystyle <_>=<_<1>>\cdot q<<\ >^>\) — уравнение членов геометрической прогрессии, где

Данная формула верна для всех значений — как положительных, так и отрицательных.

Как найти член геометрической прогрессии, зная два соседних (или равноудаленных)

Да, да, как найти значение определенного числа прогрессии, когда есть предыдущее и последующее значения членов данной прогрессии. Вспомнил?

Теперь перед нами стоит точно такой же вопрос для членов геометрической прогрессии.

Как найти член геометрической прогрессии, зная два соседних. Формула в общем виде:

\( \displaystyle <_>=\sqrt<<_>\cdot <_>>\ \), при \( \displaystyle n>2\)

Не забывай про условие при \( \displaystyle n>2\)?

Подумай, почему оно важно, например, попробуй самостоятельно просчитать \( \displaystyle <_>\ \), при \( \displaystyle n=1\). Что получится в этом случае?

Правильно, полная глупость так как формула выглядит так:

Соответственно, не забывай это ограничение.

Возьмем, к примеру, простую геометрическую прогрессию, в которой нам известны \( \displaystyle <_<2>>=6\) и \( \displaystyle <_<4>>=54\).

И посчитаем, чему же равно \( \displaystyle <_<3>>\)

Правильный ответ – \( \displaystyle <_<3>>=\pm 18\)!

Теперь, когда ты усвоил основные моменты и вывел формулу на свойство геометрической прогрессии, найди \( \displaystyle <_>\ \), зная \( \displaystyle <_>\) и \( \displaystyle <_>\)

Сравни полученные ответы с правильными:

Как найти равноудаленные члены геометрической прогрессии

Как ты думаешь, а если нам были бы даны не соседние с искомым числом значения членов геометрической прогрессии, а равноудаленные от него.

Например, нам необходимо найти \( \displaystyle <_<3>>\ \), а даны \( \displaystyle <_<1>>\ \) и \( \displaystyle <_<5>>\ \). Можем ли мы в этом случае использовать выведенную нами формулу?

Да! Формула работает не только при соседствующих с искомым членах геометрической прогрессии, но и с равноудаленными от искомого членами.

И она приобретает вид:

\( \displaystyle <_>=\sqrt<<_>\cdot <_>>\ \), при \( \displaystyle k

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Как найти неравноудаленные члены геометрической прогрессии

На самом деле это не так сложно, как кажется! Давай с тобой распишем, из чего состоит каждое данное нам и искомое числа.

Итак, у нас есть \( \displaystyle <_<3>>\) и \( \displaystyle <_<6>>\). Посмотрим, что с ними можно сделать?

Предлагаю разделить \( \displaystyle <_<6>>\) на \( \displaystyle <_<3>>\). Получаем:

Подставляем в формулу наши данные:

Следующим шагом мы можем найти \( \displaystyle q\) – для этого нам необходимо взять кубический корень из полученного числа.

\( \displaystyle <^<3>>=27\ \ \Rightarrow \ q=\sqrt[3]<27>=3\)

А теперь смотрим еще раз что у нас есть. У нас есть \( \displaystyle <_<3>>\), а найти нам необходимо \( \displaystyle <_<4>>\), а он, в свою очередь равен:

Все необходимые данные для подсчета мы нашли. Подставляем в формулу:

\( \displaystyle <_<4>>=18\cdot 3=54\)

Наш ответ: \( \displaystyle 54\).

Попробуй решить еще одну такую же задачу самостоятельно:

Дано: \( \displaystyle <_<3>>=18\), \( \displaystyle <_<5>>=648\)
Найти: \( \displaystyle <_<2>>\)

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Сумма членов геометрической прогрессии

Теперь рассмотрим формулы, которые позволяют нам быстро посчитать сумму членов геометрической прогрессии в заданном промежутке:

Чтобы вывести формулу суммы членов конечной геометрической прогрессии, умножим все части вышестоящего уравнения на \( \displaystyle q\).

Посмотри внимательно: что общего в последних двух формулах? Правильно, общие члены, например \( \displaystyle <_<2>>=<_<1>>q\) и так далее, кроме первого и последнего члена. Давай попробуем вычесть из 2-го уравнения 1-ое.

Что у тебя получилось?

Теперь вырази \( \displaystyle <_>\) через формулу члена геометрической прогрессии и подставь полученное выражение в нашу последнюю формулу:

Сгруппируй выражение. У тебя должно получиться:

Все, что осталось сделать – выразить \( \displaystyle <_>\):

Соответственно, в этом случае \( \displaystyle q\ne 1\).

А что если \( \displaystyle q=1\)? Какая формула работает тогда? Представь себе геометрическую прогрессию при \( \displaystyle q=1\). Что она из себя представляет?

Правильно ряд одинаковых чисел, соответственно формула будет выглядеть следующим образом:

Бесконечно убывающая геометрическая прогрессия

Совсем недавно мы говорили о том, что \( \displaystyle q\) может быть как больше, так и меньше нуля, однако, есть особые значения \( \displaystyle q\) при которых геометрическая прогрессия называется бесконечно убывающей.

Мы видим, что каждый последующий член меньше предыдущего в \( \displaystyle \frac<1><2>\) раза, но будет ли какое-либо число \( \displaystyle <_>=0\)?

Ты сразу же ответишь – «нет». Вот поэтому и бесконечно убывающая – убывает, убывает, а нулем никогда не становится.

Чтобы четко понять, как это выглядит визуально, давай попробуем нарисовать график нашей прогрессии. Итак, для нашего случая формула \( \displaystyle <_>=<_<1>>\cdot q<<\ >^>\) приобретает следующий вид:

На графиках нам привычно строить зависимость \( \displaystyle x\) от \( \displaystyle y\), поэтому:

Суть выражения не изменилась.

В первой записи у нас была показана зависимость значения члена геометрической прогрессии от его порядкового номера.

А во второй записи – мы просто приняли значение члена геометрической прогрессии за \( \displaystyle y\), а порядковый номер обозначили не как \( \displaystyle n\), а как \( \displaystyle x\).

Все, что осталось сделать – построить график. Посмотрим, что у тебя получилось. Вот какой график получился у меня:

Функция убывает, стремится к нулю, но никогда его не пересечет, поэтому она бесконечно убывающая.

Отметим на графике наши точки, а заодно и то, что обозначает координата \( \displaystyle x\) и \( \displaystyle y\):

Попробуй схематично изобразить график геометрической прогрессии при \( \displaystyle q=2\), если первый ее член также равен \( \displaystyle 1\).

Проанализируй, в чем разница с нашим предыдущим графиком?

Справился? Вот какой график получился у меня:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Сумма членов бесконечно убывающей геометрической прогрессии

Итак, для начала посмотрим еще раз на вот этот рисунок бесконечно убывающей геометрической прогрессии из нашего примера:

А теперь посмотрим на формулу суммы геометрической прогрессии, выведенную чуть ранее:

К чему у нас стремится \( \displaystyle <^>\)? Правильно, на графике видно, что оно стремится к нулю.

То есть при \( \displaystyle n\to \infty \), \( \displaystyle <^>\) будет почти равно \( \displaystyle 0\), соответственно, при вычислении выражения \( \displaystyle 1-<^>\) мы получим почти \( \displaystyle 1\).

В связи с этим, мы считаем, что при подсчете суммы бесконечно убывающей геометрической прогрессии, данной скобкой можно пренебречь, так как она будет равна \( \displaystyle 1\).

Формула суммы членов бесконечно убывающей геометрической прогрессии:

ВАЖНО! Формулу суммы членов бесконечно убывающей геометрической прогрессии мы используем только в том случае, если в условии в явном виде указано, что нужно найти сумму бесконечного числа членов.

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Теперь ты знаешь о геометрической прогрессии все, и настала пора переходить от теории к практике.

Самые распространенные задачи на геометрическую прогрессию, встречающиеся на экзамене – это задачи на вычисление сложных процентов.

Именно о них и пойдет речь.

Легенды и занимательные задачи на геометрическую прогрессию

Давай посмотрим как быстро Вася заразит весь класс гриппом.

Или узнаем сколько зерен будет если на каждое следующе поле шамотной доски класть в два раза больше зерен, чем на предыдущее (легенда о Сете). Какое помещение понадобиться и сколько времени нужно будет, чтобы посчитать зерна.

Или посчитаем сложные проценты, которые ты получишь, если положишь деньги в банк.

История возникновения геометрической прогрессии

Еще в древности итальянский математик Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли.

Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар?

В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: \( \displaystyle 1,\text< >2,\text< >4,\text< >8,\text< >16…\)

Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие.

Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?

В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк под сложные проценты, или при оценке скорости распространения гриппа (или коронавируса), или при… создании финансовых пирамид!

Интересно? Давай разбираться.

Как быстро Вася заразит весь класс гриппом

Ученик 5 А класса Вася, заболел гриппом, но продолжает ходить в школу. Каждый день Вася заражает двух человек, которые, в свою очередь, заражают еще двух человек и так далее. Всего в классе \( \displaystyle 31\) человек.

Через сколько дней гриппом будет болеть весь класс?

Итак, первый член геометрической прогрессии это Вася, то есть \( \displaystyle 1\) человек. \( \displaystyle 2\)-ой член геометрической прогрессии, это те два человека, которых он заразил в первый день своего прихода.

Общая сумма членов прогрессии равна количеству учащихся 5А.

Соответственно, мы говорим о прогрессии, в которой:

Подставим наши данные в формулу суммы членов геометрической прогрессии:

Весь класс заболеет за \( \displaystyle 5\) дней. Не веришь формулам и числам? Попробуй изобразить «заражение» учеников самостоятельно. Получилось?

Посчитай самостоятельно, за сколько дней ученики заболели бы гриппом, если каждый заражал бы по \( \displaystyle 3\) человека, а в классе училось \( \displaystyle 26\) человек.

Какое значение у тебя получилось? У меня получилось, что все начали болеть спустя \( \displaystyle 3\) дня.

Как ты видишь, подобная задача и рисунок к ней напоминает пирамиду, в которой каждый последующий «приводит» новых людей. Однако, рано или поздно настает такой момент, когда последние не могут никого привлечь.

В нашем случае, если представить, что класс изолирован, \( \displaystyle 16\) человек из \( \displaystyle 31\) замыкают цепочку (\( \displaystyle 51,6\%\)).

Таким образом, если бы \( \displaystyle 31\) человек были вовлечены в финансовую пирамиду, в которой деньги давались в случае, если ты приведешь двух других участников, то \( \displaystyle 16\) человек (\( \displaystyle <_<5>>=<_<1>><^<4>>\) или в общем случае \( \displaystyle <_>=<_<1>><^>\)) не привели бы никого, соответственно, потеряли бы все, что вложили в эту финансовую аферу.

Все, что было сказано выше, относится к убывающей или возрастающей геометрической прогрессии, но, как ты помнишь, у нас есть особый вид – бесконечно убывающая геометрическая прогрессия.

Как же считать сумму ее членов? И почему у данного вида прогрессии есть определенные особенности? Давай разбираться вместе.

Легенда о Сете, создателе шахмат

Узнав, что она изобретена одним из его подданных, царь решил лично наградить его. Он вызвал изобретателя к себе и приказал просить у него все, что он пожелает, пообещав исполнить даже самое искусное желание.

Царь разгневался, и прогнал Сета, сказав, что просьба слуги недостойна царской щедрости, но пообещал, что слуга получит свои зерна за все \( \displaystyle 64\) клетки доски.

А теперь вопрос: используя формулу суммы членов геометрической прогрессии, посчитай, сколько зерен должен получить Сета?

Чему равно \( \displaystyle q\) в этом случае? Правильно.

Всего клеток шахматной доски \( \displaystyle 64\). Соответственно, \( \displaystyle n=64\).

Все данные у нас есть, осталось только подставить в формулу и посчитать.

Чтобы представить хотя бы приблизительно «масштабы» данного числа, преобразуем \( \displaystyle <<2>^<64>>\), используя свойства степени:

Раскроем далее значения \( \displaystyle <<2>^<10>>\) и \( \displaystyle <<2>^<4>>\). Как ты знаешь, \( \displaystyle <<2>^<10>>=1024\), а \( \displaystyle <<2>^<4>>=64\).

Подставим данное значение в предыдущее выражение:

\( \displaystyle <<2>^<64>>=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)

Конечно, если ты хочешь, то можешь взять калькулятор и посчитать, что за число в итоге у тебя получится, а если нет, придется поверить мне на слово: итоговым значением выражения будет \( \displaystyle 18

\( \displaystyle 18\) квинтильонов \( \displaystyle 446\) квадрильонов \( \displaystyle 744\) триллиона \( \displaystyle 73\) миллиарда \( \displaystyle 709\) миллионов \( \displaystyle 551\) тысяч \( \displaystyle 615\).

Фух) Если желаете представить себе огромность этого числа, то прикиньте, какой величины амбар потребовался бы для вмещения всего количества зерна.

При высоте амбара \( \displaystyle 4\) м и ширине \( \displaystyle 10\) м длина его должна была бы простираться на \( \displaystyle 300\text< >000\text< >000\) км, — т.е. вдвое дальше, чем от Земли до Солнца.

Если бы царь был бы силен в математике, то он мог бы предложить самому ученому отсчитывать зерна, ведь чтобы отсчитать миллион зерен, ему бы понадобилось не менее \( \displaystyle 10\) суток неустанного счета, а учитывая, что необходимо отсчитать \( \displaystyle 18\) квинтильонов, зерна пришлось бы отсчитывать всю жизнь.

Задачи на вычисление сложных процентов

Ты наверняка слышал о так называемой формуле сложных процентов. Понимаешь ли ты, что она значит? Если нет, давай разбираться, так как осознав сам процесс, ты сразу поймешь, причем здесь геометрическая прогрессия.

Все мы ходим в банк и знаем, что существуют разные условия по вкладам: это и срок, и дополнительное обслуживание, и процент с двумя различными способами его начисления – простым и сложным.

С простыми процентами все более или менее понятно: проценты начисляются один раз в конце срока вклада.

То есть, если мы говорим о том, что мы кладем 100 рублей на год под \( \displaystyle 10\%\), то \( \displaystyle 10\%\) зачислятся только в конце года.

Соответственно, к окончанию вклада мы получим \( \displaystyle 110\) рублей.

Сложные проценты — это такой вариант, при котором происходит капитализация процентов, т.е. их причисление к сумме вклада и последующий расчет дохода не от первоначальной, а от накопленной суммы вклада.

Капитализация происходит не постоянно, а с некоторой периодичностью. Как правило, такие периоды равны и чаще всего банки используют месяц, квартал или год.

Допустим, что мы кладем все те же \( \displaystyle 100\) рублей по \( \displaystyle 10\%\) годовых, но с ежемесячной капитализацией вклада. Что у нас получается?

\( \displaystyle 1\) месяц — \( \displaystyle 100\cdot \left( 1+\frac<10> <100\cdot 12>\right)\)

Все ли тебе здесь понятно? Если нет, давай разбираться поэтапно.

Мы принесли в банк \( \displaystyle 100\) рублей. К концу месяца у нас на счете должна появиться сумма, состоящая из наших \( \displaystyle 100\) рублей плюс процентов по ним, то есть:

\( \displaystyle 100+100\cdot x\%\)

Мы можем вынести \( \displaystyle 100\) за скобку и тогда мы получим:

\( \displaystyle 100+100\cdot x\%=100\cdot \left( 1+x\% \right)\)

Согласись, эта формула уже больше похожа на написанную нами в начале. Осталось разобраться с процентами

В условии задачи нам сказано про \( \displaystyle 10\%\) годовых. Как ты знаешь, мы не умножаем \( \displaystyle 100\) на \( \displaystyle 10\) – мы переводим проценты в десятичные дроби, то есть:

Верно? Сейчас ты спросишь, а откуда взялось число \( \displaystyle 12\)? Очень просто!

Повторюсь: в условии задачи сказано про ГОДОВЫЕ проценты, начисление которых происходит ЕЖЕМЕСЯЧНО.

Как ты знаешь, в году \( \displaystyle 12\) месяцев, соответственно, банк будет начислять нам в месяц \( \displaystyle 12\) часть от годовых процентов:

\( \displaystyle 10\%\ ежегодно\ =\frac<10><100\cdot 12>\ ежемесячно\)

Осознал? А теперь попробуй написать, как будет выглядеть эта часть формулы, если я скажу, что проценты начисляются ежедневно.

Справился? Давай сравним результаты:

\( \displaystyle 10\%\ ежегодно\ =\frac<10><100\cdot 365>\ ежедневно\)

Вернемся к нашей задаче: напиши, сколько будет начислено на наш счет на второй месяц, с учетом, что проценты начисляются на накопленную сумму вклада.

Вот, что получилось у меня:

\( \displaystyle 100\cdot \left( 1+\frac<10> <100\cdot 12>\right)\cdot \left( 1+\frac<10> <100\cdot 12>\right)\)

Я думаю, что ты уже заметил закономерность и увидел во всем этом геометрическую прогрессию.

Напиши, чему будет равен ее \( \displaystyle 12\) член, или, иными словами, какую сумму денежных средств мы получим в конце \( \displaystyle 12\) месяца.

Источник