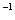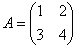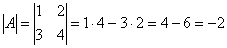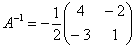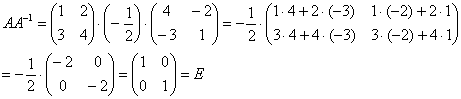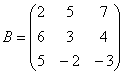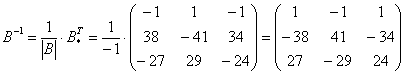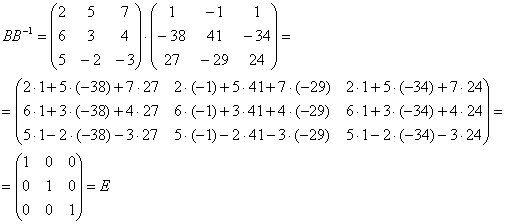Как доказать что матрица обратима

Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.

Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.

Повторение: умножение матриц

Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:

Определение индексов для клеток матрицы

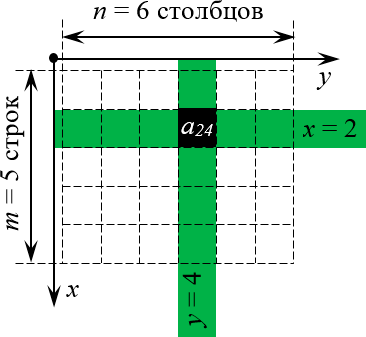
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.

В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.

Умножать можно только согласованные матрицы.

Да, вот такое суровое определение. Из него сразу следует несколько фактов:

Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.

Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)

Что такое обратная матрица

Поскольку умножение матриц — весьма трудоёмкая операция (приходится перемножать кучу строчек и столбцов), то понятие обратной матрицы тоже оказывается не самым тривиальным. И требующим некоторых пояснений.

Ключевое определение

Что ж, пора познать истину.

Казалось бы, всё предельно просто и ясно. Но при анализе такого определения сразу возникает несколько вопросов:

Насчёт алгоритмов вычисления — об этом мы поговорим чуть позже. Но на остальные вопросы ответим прямо сейчас. Оформим их в виде отдельных утверждений-лемм.

Основные свойства

\[\begin & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end\]

\[\begin & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end\]

\[\begin & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end\]

Что ж, уже неплохо. Мы видим, что обратимыми бывают лишь квадратные матрицы. Теперь давайте убедимся, что обратная матрица всегда одна.

Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:

Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.

Впрочем, мы до сих пор ничего не знаем о том, всякая ли квадратная матрица является обратимой. Тут нам на помощь приходит определитель — это ключевая характеристика для всех квадратных матриц.

Произведение двух чисел равно единице только в том случае, когда каждое из этих чисел отлично от нуля:

На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.

Но для начала сформулируем «вспомогательное» определение:

Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.

Как найти обратную матрицу

Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.

Алгебраические дополнения

Готовьтесь. Сейчас будет боль. Нет, не переживайте: к вам не идёт красивая медсестра в юбке, чулках с кружевами и не сделает укол в ягодицу. Всё куда прозаичнее: к вам идут алгебраические дополнения и Её Величество «Союзная Матрица».

Важное замечание. Вообще-то во «взрослой» математике алгебраические дополнения определяются так:

Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:

Первая мысль, возникающая в момент осознания этого определения — «это сколько же придётся всего считать!» Расслабьтесь: считать придётся, но не так уж и много.:)

Что ж, всё это очень мило, но зачем это нужно? А вот зачем.

Основная теорема

А теперь — всё то же самое, но разборчивым почерком. Чтобы найти обратную матрицу, нужно:

Задача. Найдите обратную матрицу:

\[\left[ \begin 3 & 1 \\ 5 & 2 \\\end \right]\]

Решение. Проверим обратимость. Посчитаем определитель:

\[\left| A \right|=\left| \begin 3 & 1 \\ 5 & 2 \\\end \right|=3\cdot 2-1\cdot 5=6-5=1\]

Определитель отличен от нуля. Значит, матрица обратима. Составим союзную матрицу:

Посчитаем алгебраические дополнения:

Итого наша союзная матрица выглядит так:

Осталось посчитать обратную:

Ну вот и всё. Задача решена.

Задача. Найдите обратную матрицу:

Решение. Опять считаем определитель:

Короче, союзная матрица будет выглядеть так:

Следовательно, обратная матрица будет такой:

Ну и всё. Вот и ответ.

Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:

Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.

Альтернативный способ

Элементарные преобразования

Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:

Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.

Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.

Присоединённая матрица

Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.

Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?

В чём прикол? А вот в чём:

\[\left[ A\left| E \right. \right]\to \left[ E\left| B \right. \right]\Rightarrow B=<^<-1>>\]

Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:

Задача. Найдите обратную матрицу:

Решение. Составляем присоединённую матрицу:

Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:

Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.

Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:

Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:

Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:

Осталось лишь поменять местами строки 1 и 3:

Готово! Справа — искомая обратная матрица.

Задача. Найдите обратную матрицу:

Решение. Снова составляем присоединённую:

Немного позалимаем, попечалимся от того, сколько сейчас придётся считать. и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:

Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:

Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:

Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:

И снова слева единичная матрица, значит справа — обратная.:)

Ну вот и всё. Проверку сделайте сами — мне в лом.:)

Источник

Как найти обратную матрицу?

Продолжаем разговор о действиях с матрицами. А именно – в ходе изучения данной лекции вы научитесь находить обратную матрицу. Научитесь. Даже если с математикой туго.

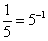
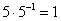
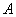
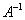
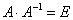
Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число . Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Однако обо всём по порядку – сначала решим важный практический вопрос, а именно, научимся эту самую обратную матрицу находить.

Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.

Есть? Тогда поехали дальше. А хотя… ехать могут все, если что-то не знаете, я буду ставить нужную ссылку по ходу объяснений.

Существует два основных метода нахождения обратной матрицы:
с помощью алгебраических дополнений и с помощью элементарных преобразований.

Сегодня мы изучим первый, более простой способ.

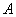
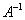
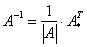
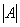
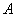
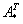
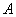
Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу . Обратную матрицу можно найти по следующей формуле:

, где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом

Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.

Найти обратную матрицу для матрицы

Решаем. Последовательность действий удобно разложить по пунктам.

1) Сначала находим определитель матрицы.

Если с пониманием сего действа плоховато, ознакомьтесь с материалом Как вычислить определитель?

Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

В рассматриваемом примере, как выяснилось, , а значит, всё в порядке.

2) Находим матрицу миноров .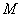

Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.

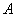
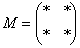
Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае .
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.

Возвращаемся к нашей матрице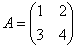
Сначала рассмотрим левый верхний элемент: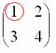

Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: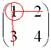

Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров: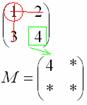

Рассматриваем следующий элемент матрицы :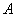

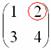
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: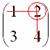

То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: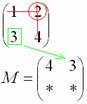

Аналогично рассматриваем элементы второй строки и находим их миноры: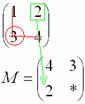


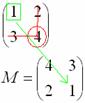
Готово.

– матрица миноров соответствующих элементов матрицы .

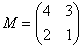
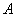
3) Находим матрицу алгебраических дополнений .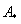

Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: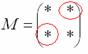

Именно у этих чисел, которые я обвел в кружок!

– матрица алгебраических дополнений соответствующих элементов матрицы .

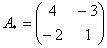
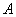
4) Находим транспонированную матрицу алгебраических дополнений .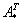

Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.

– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

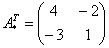
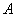
5) Ответ.

Вспоминаем нашу формулу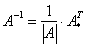
Всё найдено!

Таким образом, обратная матрица:

Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статье Действия с матрицами.

Как проверить решение?

Необходимо выполнить матричное умножение 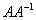либо

Проверка:

Получена уже упомянутая единичная матрица – это матрица с единицами на главной диагонали и нулями в остальных местах.

Таким образом, обратная матрица найдена правильно.

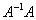
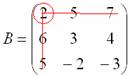
Если провести действие , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно, более подробную информацию можно найти в статье Свойства операций над матрицами. Матричные выражения. Также заметьте, что в ходе проверки константа (дробь) выносится вперёд и обрабатывается в самом конце – после матричного умножения. Это стандартный приём.

Переходим к более распространенному на практике случаю – матрице «три на три»:

Найти обратную матрицу для матрицы

Алгоритм точно такой же, как и для случая «два на два».

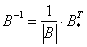
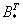
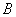
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

1) Находим определитель матрицы.

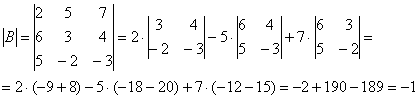
Здесь определитель раскрыт по первой строке.

Также не забываем, что 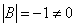, а значит, всё нормально – обратная матрица существует.

2) Находим матрицу миноров .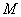

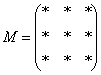
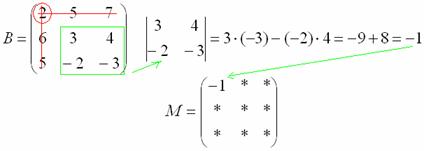
Матрица миноров имеет размерность «три на три» , и нам нужно найти девять чисел.

Я подробно рассмотрю парочку миноров:

Рассмотрим следующий элемент матрицы: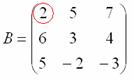

МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

Оставшиеся четыре числа записываем в определитель «два на два»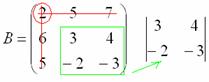

Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить: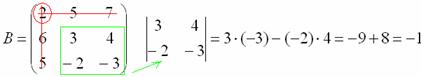

Всё, минор найден, записываем его в нашу матрицу миноров:

Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.

Ну и для закрепления – нахождение еще одного минора в картинках: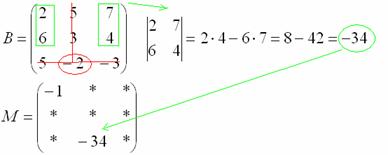

Остальные миноры попробуйте вычислить самостоятельно.

Окончательный результат:
– матрица миноров соответствующих элементов матрицы .

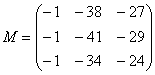
То, что все миноры получились отрицательными – чистая случайность.

3) Находим матрицу алгебраических дополнений .

В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов: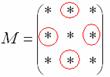

В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы .

4) Находим транспонированную матрицу алгебраических дополнений .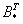

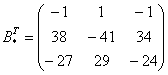
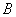
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

5) Ответ:

Проверка:

Таким образом, обратная матрица найдена правильно.

Как оформить решение на чистовик? Примерный образец чистового оформления задания можно найти на странице Правило Крамера. Метод обратной матрицы в параграфе, где идет речь о матричном методе решения системы линейных уравнений. По существу, основная часть упомянутой задачи – и есть поиск обратной матрицы.

Нахождение обратной матрицы для матрицы «четыре на четыре» не рассматриваем, так как такое задание может дать только преподаватель-садист (чтобы студент вычислил один определитель «четыре на четыре» и 16 определителей «три на три»). В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).

В ряде учебников, методичек можно встретить несколько другой подход к нахождению обратной матрицы, однако я рекомендую пользоваться именно вышеизложенным алгоритмом решения. Почему? Потому что вероятность запутаться в вычислениях и знаках – гораздо меньше.

Иногда обратную матрицу требуется найти методом Гаусса-Жордана, но второй способ доступен для студентов с приличной техникой элементарных преобразований.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник