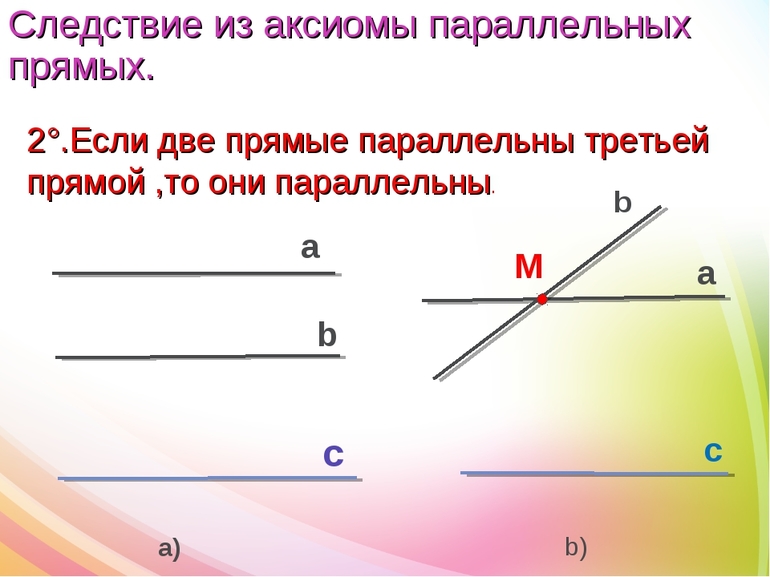
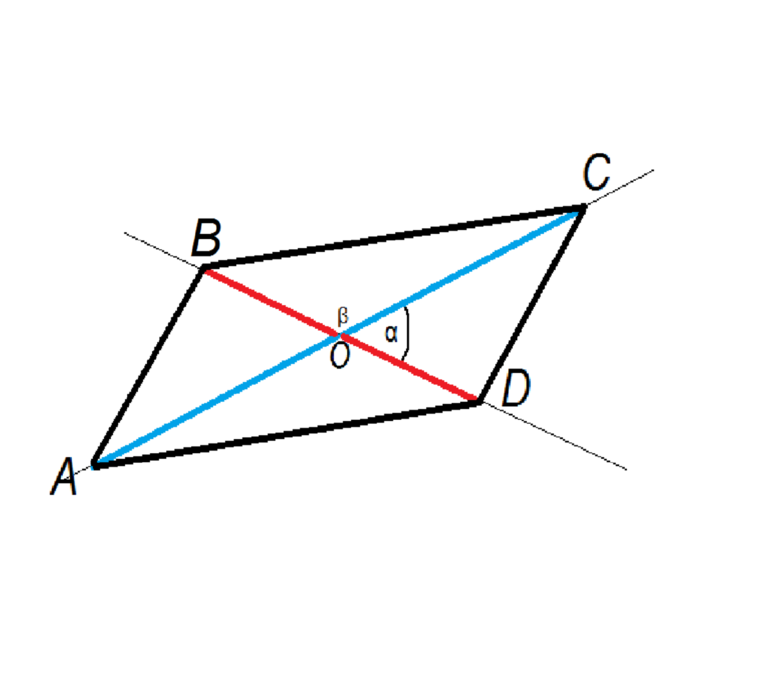
Как доказать что односторонние углы равны
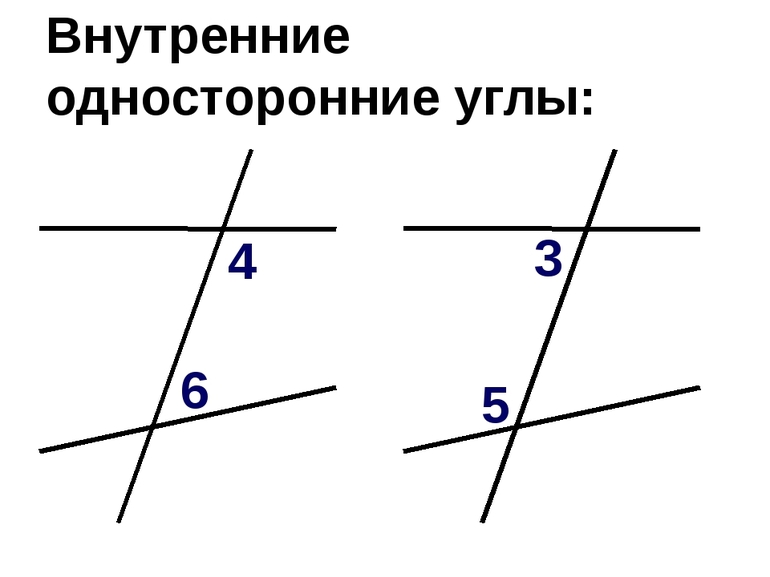
Внутренние односторонние углы
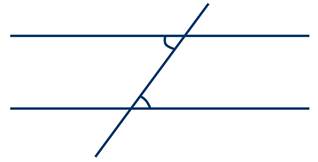
Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.
Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).
При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.

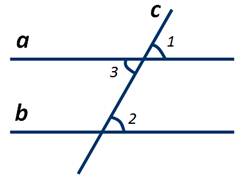
∠3 и ∠4
— внутренние односторонние углы при прямых a и b и секущей c.
Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.

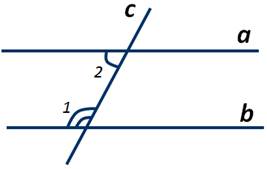
∠1 + ∠2 = 180º
(как внутренние односторонние при a ∥ b и секущей c).
Признак параллельных прямых
Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.

А так как эти углы — внутренние односторонние при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Могут ли быть внутренние односторонние углы равны?
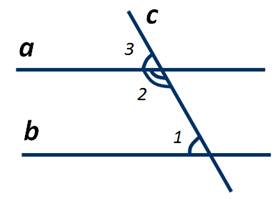
Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.

∠1 = ∠2
тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.
Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов
Урок 18. Геометрия 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов»
Вспомним теорему о равенстве накрест лежащих углов:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Пусть параллельные прямые а и b пересечены секущей c. Необходимо доказать, что соответственные углы 1 и 2 равны. Так как прямая а параллельна прямой b, то накрест лежащие углы 2 и 3 равны. ∠1 и ∠3 равны как вертикальные. Из равенств ∠2=∠3 и ∠1=∠3 следует, что ∠1=∠2. Теорема доказана.
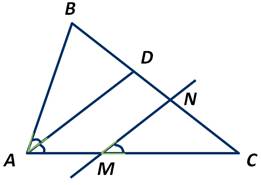
Пусть прямая MN параллельная биссектрисе AD треугольника АВС.
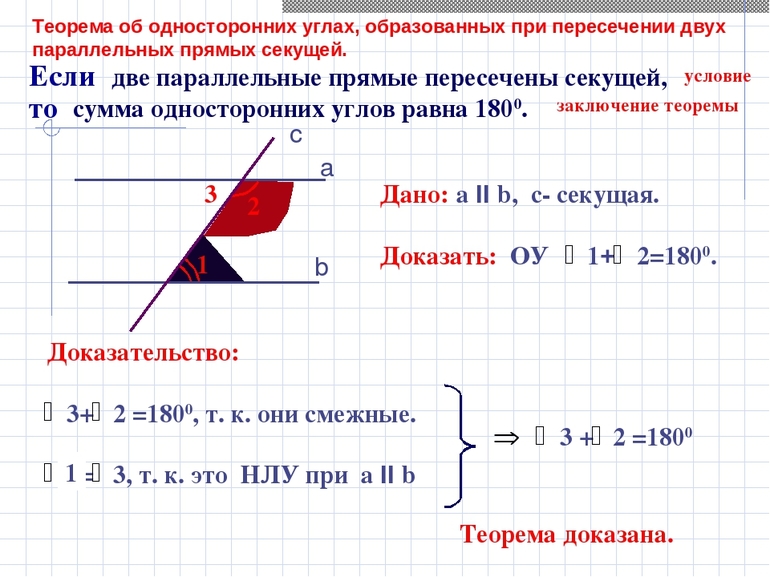
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов.
Пусть параллельные прямые а и b пересечены секущей c. Доказать, ∠1+∠2=180 градусов. Так как прямая а параллельна прямой b, то соответственные ∠1 и ∠3 равны. ∠2+∠3=180 градусов, так как углы 2 и 3 смежные. Тогда, из равенств угол ∠1=∠3 и ∠2+∠3=180 градусов, следует, что ∠1+∠2=180 градусов. Теорема доказана.
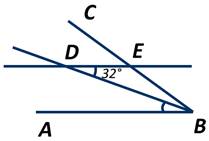
Например: пусть прямая DE параллельна стороне АВ треугольника АВС. Тогда ∠BAD+∠ADE=180 градусов.
Углы АВС и CED являются соответственными углами при параллельных прямых АВ и DE и секущей ВС, а значит, они равны. Следовательно, ∠CED=64 градуса.
Градусная мера одного из внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей, меньше градусной меры другого на 26 градусов. Вычислить градусные меры этих углов.
Пусть ∠1=x, тогда ∠2=x-26. Так как ∠1 и ∠2 являются внутренними односторонними при параллельных прямых а и b и секущей с, то их сумма равна 180 градусов, то есть ∠1+∠2=180 градусов.
Прямая линия. Признаки параллельности прямых линий.
Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия:
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
внутренние накрест лежащие углы: 3 и 5, 4 и 6;
внешние накрест лежащие углы: 1 и 7, 2 и 8;
внутренние односторонние углы: 3 и 6, 4 и 5;
внешние односторонние углы: 1 и 8, 2 и 7.
Описанные углы видны на рисунке:
Теорема.
Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся:
1. внутренние накрест лежащие углы одинаковы;
2. внешние накрест лежащие углы одинаковы;
3. соответственные углы одинаковы;
4. сумма внутренних односторонних углов будет 2d = 180 0 ;
5. сумма внешних односторонних углов будет 2d = 180 0 ;
Данную теорему иллюстрирует рисунок:
Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN.
3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8;
4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d;
5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d.
2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные.
Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.
Следовательно, ∠ 2 =∠ 8.
3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.
5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные.
Из выше доказанного обоснования получаем обратные теоремы.
Когда при пересечении двух прямых произвольной третьей прямой получим, что:
1. Внутренние накрест лежащие углы одинаковы;
или 2. Внешние накрест лежащие углы одинаковые;
или 3. Соответственные углы одинаковые;
или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;
или 5. Сумма внешних односторонних равна 2d = 180 0 ,
Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
Внутренние односторонние углы — теория, правило и свойства
Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.
Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.