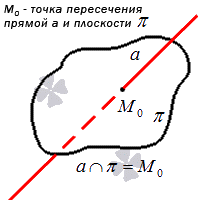
Как доказать что плоскости пересекаются по прямой

math4school.ru

Прямые и плоскости

Способы определения плоскости

Плоскость в пространстве однозначно задаётся:

тремя точками, не лежащими прямой и точкой, не лежащей

на одной прямой на этой прямой

двумя пересекающимися прямыми двумя параллельными прямыми

Прямые в пространстве

Две прямые в пространстве пересекаются, если они имеют лишь одну общую точку:

Признак параллельности прямых:

Две прямые, параллельные третьей прямой, параллельны между собой:

Прямая и плоскость в пространстве

Если каждая точка прямой принадлежит плоскости, то говорят, что и прямая принадлежит плоскости:

Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости:

Говорят, что прямая и плоскость пересекаются, если они имеют одну единственную общую точку:

Прямая и плоскость называются параллельными, если они не имеют общих точек:

Плоскость и не лежащая на ней прямая либо пересекаются (в одной точке), либо не пересекаются (параллельны).

Признак параллельности прямой и плоскости:

Прямая, не лежащая в плоскости, параллельна этой плоскости тогда и только тогда, когда она параллельна некоторой прямой в этой плоскости:

Признак параллельности прямых:

Признак параллельности прямых:

Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии пересечения этих плоскостей:

Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения этой прямой и плоскости.

Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

Признак перпендикулярности прямой и плоскости:

Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости:

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой прямой:

Прямые, перпендикулярные одной плоскости, – параллельны:

Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, которые соединяет эту точку с точкой плоскости (основанием перпендикуляра) и лежит на прямой, которая перпендикулярна плоскости. Длину перпендикуляра, проведённого из данной точки к данной плоскости, считают расстоянием между этими точкой и плоскостью.

Наклонной, проведённой из данной точки к плоскости, называется любой отрезок, который соединяет эту точку с точкой плоскости (основанием перпендикуляра) и не является перпендикуляром, проведённым к этой плоскости.

Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых к плоскости из одной точки, называется проекцией (ортогональной проекцией) этой наклонной на плоскость.

АВ – перпендикуляр, проведённый из точки А к плоскости α ;

АС – наклонная, проведённая из точки А к плоскости α ;

В – основание перпендикуляра АВ ;

С – основание наклонной АС ;

ВС – проекция наклонной АС на плоскость α .

Свойства перпендикуляра и наклонной:

Углом между наклонной и плоскость называется величина угла между наклонной и её ортогональной проекцией на эту плоскость:

Угол между наклонной и её ортогональной проекцией на плоскость меньше угла между этой наклонной и любой другой прямой, проходящей в этой плоскости через основание наклонной:

Теорема про три перпендикуляра:

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной. И наоборот: если прямая, проведённая на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной:

Расстоянием от прямой до параллельной ей плоскости называется расстояние от любой точки этой прямой до плоскости:

Отрезок АВ – общий перпендикуляр прямой а и плоскости α.

Общим перпендикуляром двух скрещивающихся прямых ( a и b ) называется отрезок ( АВ ) с концами на этих прямых, являющийся перпендикуляром к каждой из них.

Две скрещивающиеся прямые всегда имеют общий перпендикуляр, и притом только один.

Длина общего перпендикуляра двух скрещивающихся прямых считается расстоянием между ними:

Плоскости в пространстве

Говорят, что две плоскости пересекаются, если в одной из них существуют точки как принадлежащие другой плоскости, так и не принадлежащие ей.

Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку:

Говорят, что две плоскости совпадают, если каждая точка одной плоскости является точкой другой, и наоборот:

Две плоскости называются параллельными, если они не имеют общих точек:

Через точку вне плоскости можно провести плоскость параллельную данной и притом только одну.

Признак параллельности плоскостей:

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны:

Расстоянием между двумя параллельными плоскостями называется расстояние от любой точки одной плоскости до другой плоскости.

Длина некоторого отрезка выражает расстояние между двумя параллельными плоскостями, если этот отрезок является общим перпендикуляром этих плоскостей:

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой.

Полуплоскости, о которых шла речь, называются гранями двугранного угла, а прямая – ребром двугранного угла:

α и β – грани, KL – ребро двугранного угла.

Все линейные углы данного двугранного угла совмещаются параллельным переносом и равны.

Мера линейного угла служит мерой и двугранного угла, которому этот линейный угол соответствует.

Линейные углы, соответствующие равным двугранным углам, равны. И наоборот: равным линейным углам соответствуют равные двугранные углы.

Углом между двумя пересекающимися плоскостями называется наименьшая из мер двухгранных углов, образованных этими плоскостями.

Две плоскости называются перпендикулярными ( α⊥β ), если угол между ними равен 90°.

Угол между параллельными плоскостями считается равным 0°.

Если φ – величина угла между некоторыми двумя плоскостями, то

Признак перпендикулярности плоскостей:

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны:

Прямая, проведённая в одной из двух перпендикулярных плоскостей перпендикулярно линии их пересечения, перпендикулярна другой плоскости:

Некоторые свойства прямых и плоскостей

Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны:

Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость; более того, эта прямая образует с параллельными плоскостями равные углы:

Прямые, полученные при пересечении двух параллельных плоскостей третьей плоскостью, параллельны между собой:

Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости:

Две плоскости, перпендикулярные одной и той же прямой, параллельны:

Плоскость, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости:

Источник

Пересекающиеся плоскости

Плоскость — это одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Линия пересечения двух плоскостей — это прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Содержание:

Понятие пересекающихся плоскостей

Определение. Плоскости, которые имеют хотя бы одну общую точку, называют пересекающимися.

Аксиома 5. Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

При этом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой . Плоскости и в этом случае являются пересекающимися по прямой (рис. 2.379).

Пример:

Дана плоскость . Доказать, что существует другая плоскость (3, пересекающая .

Решение:

Из условия задачи имеем:

1. Плоскость (дано) (рис. 2.380).

2. Нужно доказать, что существует другая плоскость , пересекающая .

Мы знаем, что на основании аксиомы 3 (аксиомы плоскости) три точки определяют единственную плоскость.

3. Возьмем точки А и В, принадлежащие плоскости , и точку С, не лежащую на прямой АВ и не принадлежащую (построение) (рис. 2.381).

4. Точки А, В и С не лежат на одной прямой. Через них можно провести плоскость , и притом только одну (3, аксиома 3).

5. Плоскости и имеют общую точку (1, 3, 4).

6. Плоскости и пересекаются по прямой АВ (5, аксиома 5) (рис. 2.382).

7. Мы доказали, что существует плоскость Р, пересекающая . (6)

Замечание. Если допустить, что точка С лежит на прямой АВ, то она будет лежать и в плоскости , что противоречит выбору точки С.

Двугранные углы

При пересечении плоскостей образуются двугранные углы.

Определение. Фигуру, образованную двумя полуплоскостями, исходящими из одной прямой, называют двугранным углом. Прямую называют ребром, а полуплоскости — сторонами или гранями двугранного угла.

На рисунке 2.383 изображен двугранный угол с ребром АВ.

Этот угол можно обозначать двумя буквами, поставленными у его ребра (двугранный угол АВ). Но если при одном ребре лежит несколько двугранных углов, то каждый из них обозначают четырьмя буквами, из которых две средние стоят при ребре, одна крайняя — у одной грани, другая — у другой (рис. 2.384).

Определение. Если через произвольную точку ребра двугранного угла провести плоскость, перпендикулярную ребру, то в пересечении этой плоскости с двугранным углом образуется угол, который называют линейным углом двугранного угла.

На рисунке 2.385 изображен линейный угол АОВ двугранного угла АОСВ. Вершиной линейного угла служит точка О, лежащая на ребре ос двугранного угла, а сторонами — лучи граней, исходящие из точки о и перпендикулярные ребру двугранного угла.

Двугранный угол имеет бесконечное множество линейных углов (рис. 2.386).

Определение. Градусной мерой двугранного угла называют градусную меру любого из его линейных углов.

Определение. Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).

Можно доказать следующее утверждение.

Теорема 1. Все линейные углы двугранного угла равны друг другу.

Для двугранных углов так же, как и для плоских, вводится понятие его градусной меры — величины.

Определение. Два двугранных угла называют равными, если они имеют одну и ту же градусную меру.

Если градусная мера одного из двугранных углов больше градусной меры другого, то говорят, что первый двугранный угол больше второго, а второй меньше первого. На рисунке 2.387 изображены три двугранных угла с общим ребром АВ. Двугранные углы CABD и DABE равны, так как их градусные меры равны 30°. Двугранный угол САВЕ больше двугранного угла CABD.

Подобно плоским углам, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

Все сказанное можно сформулировать в виде теорем.

Теорема 2. 1. Равным двугранным углам соответствуют равные линейные углы.

2. Большему двугранному углу соответствует больший линейный угол.

Верна и обратная теорема.

Теорема 3. 1. Равным линейным углам соответствуют равные двугранные углы.

2. Большему линейному углу соответствует больший двугранный угол.

Из теорем 2 и 3 легко получить три следствия.

Следствие 1. Прямому двугранному углу соответствует прямой линейный угол, и обратно.

Следствие 2. Все прямые двугранные углы равны, потому что у них равны линейные углы.

Следствие 3. Вертикальные двугранные углы равны.

Пример:

Из условия теоремы имеем:

1. PABQ и — два данных двугранных угла (рис. 2.388).

2. Вложим угол в угол АВ так, чтобы ребро совпало с ребром АВ, а грань — с гранью Р (построение) (рис. 2.389).

3. Если эти двугранные углы равны, то грань совпадает с Q; если же двугранные углы не равны, то грань займет некоторое положение, не совпадающее с Q, например положение (1, 2).

4. Возьмем на общем ребре какую-нибудь точку В и проведем через нее плоскость , перпендикулярную ребру АВ (построение) (рис. 2.390).

5. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы.

Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол cbd; если же двугранные углы не совпадут (если, например, грань займет положение то у большего двугранного угла окажется больший линейный угол (именно ) (3, 4).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник

Данная глава рассказывает о том, как найти координаты точки пересечения прямой с плоскостью при заданных уравнениях, определяющих эту плоскость. Будет рассмотрено понятие точки пересечения прямой с плоскостью, два способа нахождения координат точки пересечения прямой с плоскостью.

Точка пересечения прямой и плоскости – определение

Для углубленного изучения теории необходимо начать рассмотрение с понятия точки, прямой, плоскости. Понятие о точке, прямой линии рассматривается как на плоскости, так и в пространстве. Для детального рассмотрения необходимо обратиться к теме о прямой и плоскости в пространстве.

Существует несколько вариаций расположения прямой относительно плоскости и пространства:

Если рассмотреть третий случай, то отчетливо видно, что прямая с плоскостью при пересечении образуют общую точку, которую называют точкой пересечения прямой и плоскости. рассмотрим данный случай на примере.

Нахождение координат точки пересечения прямой и плоскости

Была введена прямоугольная система координат О х у z трехмерного пространства. Каждая прямая имеет свое собственное уравнение, а каждая плоскость соответствует своему заданному уравнению, каждая точка имеет определенное количество действительных чисел – координат.

Чтобы подробно разобраться в теме координат пересечения, необходимо знать все виды уравнения прямой в пространстве и уравнений плоскости. в данном случае пригодятся знания о переходе от одного вида уравнения к другому.

Рассмотрим задачу, которая основывается на заданном пересечении прямой и плоскости. она сводится к нахождению координат пересечений.

Когда точка принадлежит некоторой прямой, координаты точки пересечения являются решением обоих уравнения. Из определения имеем, что при пересечении образуется общая точка. Для решения задания необходимо подставить в оба уравнения координаты точки М 0 и вычислить. Если она является точкой пересечения, то оба уравнения будут соответствовать.

Ответ: заданная точка с координатами является точкой пересечения.

Если координаты точки пересечения являются решением обоих уравнений, то они пересекаются.

Первый способ нахождения координат пересечения прямой и плоскости.

Необходимые нам координаты прямой a и плоскости α должны удовлетворять обоим уравнениям. Таким образом задается система линейных уравнений, имеющая вид

A x + B y + C z + D = 0 A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Следует обратить внимание на тему решения систем линейных уравнений.

Так как определитель матрицы не равен нулю, система имеет только одно решение. Для этого мы применим метод Крамера. Он считается очень удобным и подходящим для данного случая.

Ответ: нет координат точки пересечения.

Применив метод Гауса, стало понятно, что равенство неверное, так как система уравнений решений не имеет.

Ответ: нет точек пересечения, так как прямая параллельна плоскости.

Подробнее этот способ будет рассмотрен на примерах, приведенных ниже.

Для решения системы, необходимо произвести подстановку. Тогда получаем, что

Источник