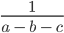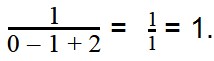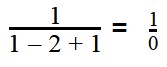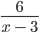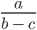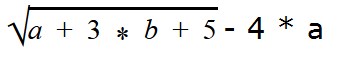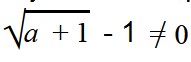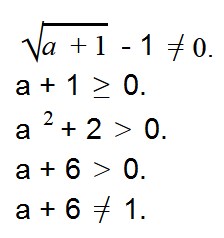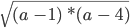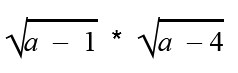Как доказать что при всех допустимых значениях переменной
Область допустимых значений функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 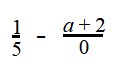
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.