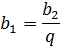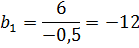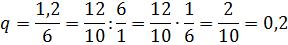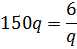Как доказать что прогрессия геометрическая

Как доказать что прогрессия геометрическая

Коды ОГЭ по математике: 4.2.3. Геометрическая прогрессия. Формула общего члена геометрической прогрессии. 4.2.4. Формула суммы первых нескольких членов геометрической прогрессии

Определения и обозначения

В геометрической прогрессии отношение любого члена, начиная со второго, к предыдущему члену равно одному и тому же числу. Это число называют знаменателем геометрической прогрессии и обозначают буквой q. Правило, по которому образуются члены геометрической прогрессии, можно записать в виде рекуррентной формулы:

Или b_n+1 = b_n • q.

Пример 1. Пусть b₁ = 1 и q = 3. Получаем геометрическую прогрессию: 1; 3; 9; 27; 81; 243; … Это возрастающая последовательность.

Геометрическая прогрессия, члены которой – положительные числа, обладает свойством: любой её член, начиная со второго, равен среднему геометрическому предыдущего и последующего членов, т. е.

Формулы n–го члена геометрической прогрессий

Формула n–го члена геометрической прогрессии (b_n), первый член которой равен b₁, a знаменатель равен q:

b_n = b₁ • q n–1

Формула содержит три переменные. Если известны значения двух из них, то можно вычислить и значение третьей.

Пример 3. В геометрической прогрессии b₃ = –1/2, b₆ = 4. Найдём b₁₂.

Изображение членов геометрической прогрессии
точками на координатной плоскости

Члены числовой последовательности можно изображать точками на координатной плоскости. Для этого по горизонтальной оси откладывают номер члена, a по вертикальной – соответствующий член последовательности.

Формула суммы первых n членов геометрической прогрессии

Если q ≠ 1, то

Заметим, что если 0

Это конспект по математике на тему «Геометрическая прогрессия». Выберите дальнейшие действия:

Источник

Геометрическая прогрессия: определение, формулы, свойства

Сумма членов геометрической прогрессии

b₁ — первый член прогрессии,

q — знаменатель прогрессии,

Для нахождения суммы членов геометрической прогрессии вы можете воспользоваться нашим онлайн калькулятором. Просто введите данные и получите результат.

Знаменатель геометрической прогрессии

Знаменатель геометрической прогрессии можно вычислить с помощью текущего и следующего членов геометрической прогрессии по формуле:

Члены геометрической прогрессии

Общая формула для вычисления n-ого члена геометрической прогрессии по первому члену и знаменателю:

Следующий член геометрической прогрессии можно найти по предыдущему члену и знаменателю:

Предыдущий член геометрической прогрессии можно найти по следующему члену и знаменателю:

Также член геометрической прогрессии можно найти, если известны следующий и предыдущий члены:

Для чего нужна геометрическая прогрессия и ее история возникновения.

Еще в древности итальянский математик монах Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли. Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар? В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие. Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?

Есть еще много простых случаев, где применяется геометрическая прогрессия. Например, распространение гриппа: один человек заразил человек, те в свою очередь заразили еще по человека, и таким образом вторая волна заражения – человек, а те в свою очередь, заразили еще

Общий вид геометрической прогрессии

Члены прогрессии:

Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.

Виды прогрессии:

Формула суммы n-первых членов геометрической прогрессии

Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q| , называется геометрической прогрессией. Число , называется геометрической прогрессией. Число называется знаменателем прогрессии.

То есть геометрическая прогрессия определяется рекуррентным соотношением

Примеры геометрических прогрессий.

Теорема 1. Пусть — геометрическая прогрессия со знаменателем — геометрическая прогрессия со знаменателем Тогда для всех натуральных справедлива формула

Доказательство. Воспользуемся рекуррентным определением геометрической прогрессии:

Итак, для n-го члена геометрической прогрессии справедлива формула

Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:

Доказательство. Из определения геометрической прогрессии

Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.

Пример 1. Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвёртого членов — 30. Найдём первый член и знаменатель прогрессии.

Решение. По условию

Выразим члены геометрической прогрессии через и и : Тогда система запишется в виде

Разделив второе уравнение системы на первое, получим Следовательно, Следовательно,

Бесконечно убывающая геометрическая прогрессия.

Совсем недавно мы говорили о том, что может быть как больше, так и меньше нуля, однако, есть особые значения при которых геометрическая прогрессия называется бесконечно убывающей.

Чтобы четко понять, как это выглядит визуально, давай попробуем нарисовать график нашей прогрессии. Итак, для нашего случая формула приобретает следующий вид:

Видишь? Функция убывает, стремится к нулю, но никогда его не пересечет, поэтому она бесконечно убывающая. Отметим на графике наши точки, а заодно и то, что обозначает координата и :

Справился? Вот какой график получился у меня:

Теперь, когда ты полностью разобрался в основах темы геометрической прогрессии: знаешь, что это такое, знаешь, как найти ее член, а также знаешь, что такое бесконечно убывающая геометрическая прогрессия, перейдем к ее основному свойству.

Источник

Геометрическая прогрессия

Что нужно знать

Что вы узнаете

Геометрическая прогрессия

Выберите из перечисленных ниже последовательностей геометрическую прогрессию:

Из этой формулы следует такое равенство:

Не арифметическая и не геометрическая прогрессия

Решите теперь следующую задачу:

Сумма первых n n n членов геометрической прогрессии

Среди заданий 11 ЕГЭ не бывает задач на сумму геометрической прогрессии. Однако эту тему полезно знать для решения более сложных экзаменационных и практических задач.

Формула суммы геометрической прогрессии оказывается очень полезной для решения практических задач, особенно в области финансов.

Например, если выручка компании увеличивается каждый год на определенный процент, то суммарная выручка за 1 0 10 1 0 лет — это сумма геометрической прогрессии.

Сумму геометрической прогрессии со знаменателем q ≠ 1 q\neq 1 q ≠ 1 можно найти по формуле:

Доказать эту формулу несколько сложнее, чем формулу суммы арифметической прогрессии. Тем не менее полезно познакомиться с ее доказательством.

Докажем утверждение по индукции.

Метод математической индукции позволяет доказывать и значительно более сложные утверждения.

Решите задачу с помощью этой формулы:

Дисконтированный денежный поток (дополнительно)

Еще одно важное применение геометрической прогрессии в финансах — расчет суммы приведенных (дисконтированных) денежных потоков. Если вы усвоите этот принцип, вам будет понятно, как финансисты рассчитывают справедливую стоимость актива (не важно, какого: акции, слитка золота, выданного кредита или даже коровы, которая дает молоко).

Мы называем денежным потоком любую сумму денег, которую получает (или планирует получить) человек или фирма в определенный период времени (например, в течение 2 0 1 5 2015 2 0 1 5 года). Будем называть человека, который ожидает получить денежный поток, инвестором.

Конечно же, прямо сейчас! Даже если вам не на что тратить эти деньги прямо сейчас, вы можете положить их в банк под процент и через год получить уже больше, чем 1 0 0 0 1000 1 0 0 0 рублей. Например, если банк принимает депозиты под 1 0 % 10\% 1 0 % годовых, через год у вас будет 1 1 0 0 1100 1 1 0 0 рублей.

Рассмотрим еще один пример:

Бесконечная геометрическая прогрессия

Заключение

Задачи с арифметическими и геометрическими прогрессиями часто встречаются на практике. Если в условии говорится об увеличении на одну и ту же величину, то речь идет об арифметической прогрессии. Если же происходит увеличение в одно и то же число раз, либо на одно и то же число процентов, то речь идет о геометрической прогрессии.

Следующие формулы позволяют решить практически любую задачу на прогрессии:

Источник

Что такое геометрическая прогрессия? Основные понятия.

Что такое геометрическая прогрессия? Понятие геометрической прогрессии.

Начинаем экскурсию, как обычно, с элементарщины. Пишу незаконченную последовательность чисел:

1, 10, 100, 1000, 10000, …

Сможете уловить закономерность и сказать, какие числа пойдут дальше? Ясен перец, дальше пойдут числа 100000, 1000000 и так далее. Даже без особого умственного напряжения всё ясно, правда ведь?)

Ладно. Ещё пример. Пишу вот такую последовательность:

Сможете сказать, какие числа пойдут дальше, вслед за числом 16 и назвать восьмой член последовательности? Если вы сообразили, что это будет число 128, то очень хорошо. Значит, полдела в понимании смысла и ключевых моментов геометрической прогрессии уже сделано. Можно расти дальше.)

А теперь снова переходим от ощущений к строгой математике.

Ключевые моменты геометрической прогрессии.

Геометрическая прогрессия — это последовательность чисел. Как и арифметическая прогрессия. Ничего хитрого. Только устроена эта последовательность по-другому. Отсюда, естественно, и другое название носит, да…

Со вторым ключевым моментом вопрос похитрее будет. Давайте вернёмся чуть назад и вспомним ключевое свойство арифметической прогрессии. Вот оно: каждый член отличается от предыдущего на одну и ту же величину.

А можно ли похожее ключевое свойство сформулировать для геометрической прогрессии? Подумайте немного… Присмотритесь к приведённым примерам. Догадались? Да! В геометрической прогрессии (любой!) каждый её член отличается от предыдущего в одно и то же число раз. Всегда!

В первом примере это число — десятка. Какой член последовательности ни возьми, он больше предыдущего в десять раз.

Во втором примере это — двойка: каждый член больше предыдущего в два раза.

Именно этим ключевым моментом геометрическая прогрессия и отличается от арифметической. В арифметической прогрессии каждый следующий член получается прибавлением одной и той же величины к предыдущему члену. А здесь — умножением предыдущего члена на одну и ту же величину. Вот и вся разница.)

Этот ключевой момент полностью идентичен таковому для арифметической прогрессии. А именно: каждый член геометрической прогрессии стоит на своём месте. Всё точь-в-точь как и в арифметической прогрессии и комментарии, я думаю, излишни. Есть первый член, есть сто первый и т.д. Переставим местами хотя бы два члена — закономерность (а вместе с ней и геометрическая прогрессия) исчезнут. Останется просто последовательность чисел безо всякой логики.

Вот и всё. Вот и весь смысл геометрической прогрессии.

Термины и обозначения.

А вот теперь, разобравшись со смыслом и ключевыми моментами геометрической прогрессии, можно и к теории переходить. А иначе какая же теория без понимания смысла, правда?

Как обозначать геометрическую прогрессию?

Как записывается геометрическая прогрессия в общем виде? Никаких проблем! Каждый член прогрессии также записывается в виде буквы. Только для арифметической прогрессии, обычно, используется буква «а», для геометрической — буковка «b». Номер члена, как обычно, указывается индексом справа внизу. Сами члены прогрессии просто перечисляем через запятую или точку с запятой.

Коротко такую прогрессию записывают вот так: (b_n).

Или вот так, для конечных прогрессий:

Или, в краткой записи:

Вот, собственно, и все обозначения. Всё то же самое, только буква другая, да.) А теперь переходим непосредственно к определению.

Определение геометрической прогрессии.

Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый последующий член равен предыдущему члену, умноженному на одно и то же ненулевое число.

Вот и всё определение. Большинство слов и фраз вам понятны и хорошо знакомы. Если, конечно, понимаете смысл геометрической прогрессии «на пальцах» и числовой последовательности вообще. Но есть и несколько новых фраз, на которые я хотел бы обратить особое внимание.

Во-первых, слова: «первый член которой отличен от нуля«.

Это ограничение на первый член введено не случайно. Как вы думаете, что произойдёт, если первый член b₁ окажется равным нулю? Чему будет равен второй член, если каждый член больше предыдущего в одно и то же число раз? Допустим, в три раза? Посмотрим… Умножаем первый член (т.е. 0) на 3 и получаем… ноль! А третий член? Тоже ноль! И четвёртый член — тоже ноль! И так далее…

Получаем просто мешок баранок последовательность нулей:

Конечно, такая последовательность имеет право на жизнь, но никакого практического интереса она не представляет. Всё и так понятно. Любой её член — ноль. Сумма любого количества членов — тоже ноль… Что с ней интересного можно делать? Ничего…

Следующие ключевые слова: «умноженному на одно и то же ненулевое число».

Это самое число тоже носит своё специальное название — знаменатель геометрической прогрессии. Начинаем знакомство.)

Знаменатель геометрической прогрессии.

Всё проще простого.

Знаменатель геометрической прогрессии — это ненулевое число (или величина), показывающее, во сколько раз каждый член прогрессии больше предыдущего.

Опять же, по аналогии с арифметической прогрессией, ключевым словом, на которое следует обратить внимание в этом определении, является слово «больше». Оно означает, что каждый член геометрической прогрессии получается умножением на этот самый знаменатель предыдущего члена.

Для расчёта, скажем, второго члена, надо взять первый член и умножить его на знаменатель. Для расчёта десятого члена, надо взять девятый член и умножить его на знаменатель.

И так далее и тому подобное…

Сам знаменатель геометрической прогрессии может при этом быть каким угодно. Совершенно любым! Целым, дробным, положительным, отрицательным, иррациональным — всяким. Кроме нуля. Об этом и говорит нам слово «ненулевое» в определении. Зачем это слово тут нужно — об этом далее.

Знаменатель геометрической прогрессии обозначается, чаще всего, буковкой q.

Определим, например, величину q для такой геометрической прогрессии:

Всё элементарно. Берём любое число последовательности. Какое хотим, такое и берём. Кроме самого первого. Например, 18. И делим на предыдущее число. То есть, на 6.

Вот и всё. Это верный ответ. Для данной геометрической прогрессии знаменатель равен трём.

Найдём теперь знаменатель q для другой геометрической прогрессии. Например, вот такой:

И все дела.) В этот раз знаменатель прогрессии оказался отрицательным. Минус два. Бывает.)

Возьмём теперь вот такую прогрессию:

И снова, вне зависимости от вида чисел, стоящих в последовательности (хоть целые, хоть дробные, хоть отрицательные, хоть иррациональные), берём любое число (например, 1/9) и делим на предыдущее число (1/3). По правилам действий с дробями, естественно.

И всё.) Здесь знаменатель оказался дробным: q = 1/3.

А вот такая «прогрессия» как вам?

Очевидно, здесь q = 1. Формально это тоже геометрическая прогрессия, только с одинаковыми членами.) Но такие прогрессии для изучения и практического применения не интересны. Так же, как и прогрессии со сплошными нулями. Поэтому мы их рассматривать и не будем.

Как вы видите, знаменатель прогрессии может быть каким угодно — целым, дробным, положительным, отрицательным — всяким! Не может быть только нулём. Не догадались, почему?

Ну, давайте на каком-нибудь конкретном примере посмотрим, что будет, если взять в качестве знаменателя q нолик.) Пусть у нас, допустим, будет b₁ = 2, а q = 0. Чему тогда будет равен второй член?

Ну что, стоит считать дальше или нет? Я думаю, уже каждому… эээ-э-э… В общем, каждому ясно, что все последующие члены (кроме, быть может, первого), будут нулями… И чем нам такая последовательность интересна? Ничем.) Вот и не рассматривают нулевой знаменатель в геометрической прогрессии. Так же, как и не рассматривают нулевой первый член, да.)

Виды и поведение геометрических прогрессий.

С арифметической прогрессией всё было более-менее ясно: если разность прогрессии d положительна, то прогрессия возрастает. Если же разность отрицательна, то прогрессия убывает. Всего два варианта. Третьего не дано.)

А вот с поведением геометрической прогрессии всё будет уже гораздо интереснее и разнообразнее!)

Как только себя тут члены ни ведут: и возрастают, и убывают, и неограниченно приближаются к нулю, и даже меняют знаки, попеременно бросаясь то в «плюс», то в «минус»! И во всём этом многообразии надо уметь хорошо разбираться, да…

Разбираемся?) Начинаем с самого простого случая.

Знаменатель положительный (q>0)

При положительном знаменателе, во-первых, члены геометрической прогрессии могут уходить в плюс бесконечность (т.е. неограниченно возрастать) и могут уходить в минус бесконечность (т.е. неограниченно убывать). К такому поведению прогрессий мы уже попривыкли.

Здесь всё просто. Каждый член прогрессии получается больше предыдущего. Причём каждый член получается умножением предыдущего члена на положительное число +2 (т.е. q = 2). Поведение такой прогрессии очевидно: все члены прогрессии неограниченно растут, уходя в космос. В плюс бесконечность…

А теперь вот такая прогрессия:

Здесь тоже каждый член прогрессии получается умножением предыдущего члена на положительное число +2. А вот поведение такой прогрессии уже прямо противоположное: каждый член прогрессии получается меньше предыдущего, и все её члены неограниченно убывают, уходя в минус бесконечность.

А теперь давайте подумаем: что общего у этих двух прогрессий? Правильно, знаменатель! И там и там q = +2. Положительное число. Двойка. А вот поведение этих двух прогрессий — принципиально разное! Не догадались, почему? Да! Всё дело в первом члене! Именно он, как говорится, и заказывает музыку.) Смотрите сами.

В первом случае первый член прогрессии положительный (+1) и, стало быть, все последующие члены, получаемые умножением на положительный знаменатель q = +2, также будут положительными.

А вот во втором случае первый член отрицательный (-1). Поэтому и все последующие члены прогрессии, получаемые умножением на положительное q = +2, также будут получаться отрицательными. Ибо «минус» на «плюс» всегда даёт «минус», да.)

Как вы видите, в отличие от арифметической прогрессии, геометрическая прогрессия может вести себя совершенно по-разному не только в зависимости от знаменателя q, но ещё и в зависимости от первого члена, да.)

Запоминаем: поведение геометрической прогрессии однозначно определяется её первым членом b₁ и знаменателем q.

А теперь начинаем разбор менее привычных, но зато гораздо более интересных случаев!

Возьмём, например, вот такую последовательность:

Эта последовательность — тоже геометрическая прогрессия! Каждый член этой прогрессии тоже получается умножением предыдущего члена, на одно и то же число. Только число это — дробное: q = +1/2. Или +0,5. Причём (важно!) число, меньшее единички: q = 1/2

Чем интересна эта геометрическая прогрессия? Куда стремятся её члены? Давайте посмотрим:

Что интересного здесь можно заметить? Во-первых, сразу бросается в глаза убывание членов прогрессии: каждый её член меньше предыдущего ровно в 2 раза. Или, в соответствии с определением геометрической прогрессии, каждый член больше предыдущего в 1/2 раза, т.к. знаменатель прогрессии q = 1/2. А от умножения на положительное число, меньшее единички, результат обычно уменьшается, да…

Что ещё можно заметить в поведении этой прогрессии? Убывают ли её члены неограниченно, уходя в минус бесконечность? Нет! Они убывают по-особенному. Сначала довольно быстро убывают, а потом всё медленнее и медленнее. Причём всё время оставаясь положительными. Пускай и очень-очень маленькими. А к чему же они сами при этом стремятся? Не догадались? Да! К нулю они стремятся!) Причём, обратите внимание, самого нуля члены нашей прогрессии никогда не достигают! Только лишь бесконечно близко к нему приближаются. Это очень важно.)

Похожая ситуация будет и в такой прогрессии:

Итак, мы рассмотрели все возможные положительные знаменатели — и большие единички и меньшие единички. Саму единичку в качестве знаменателя мы не рассматриваем по причинам, изложенным выше (вспомните пример с последовательностью троек…)

Если знаменатель геометрической прогрессии положителен и больше единицы (q>1), то члены прогрессии:

a ) неограниченно возрастают (если b₁>0);

б) неограниченно убывают (если b₁

Если знаменатель геометрической прогрессии положителен и меньше единицы (0

а) бесконечно близко приближаются к нулю сверху (если b₁>0);

б) бесконечно близко приближаются к нулю снизу (если b₁

Осталось теперь рассмотреть случай отрицательного знаменателя.

Знаменатель отрицательный (q

Получим вот такую последовательность:

Куда же стремятся её члены? А никуда.) Да, по абсолютной величине (т.е. по модулю) члены нашей прогрессии неограниченно возрастают (отсюда и название «возрастающая»). Но при этом каждый член прогрессии поочерёдно бросает то в жар, то в холод. То в «плюс», то в «минус». Колеблется наша прогрессия… Причём размах колебаний с каждым шагом стремительно растёт, да.) Стало быть, стремления членов прогрессии куда-то конкретно здесь нет. Ни к плюс бесконечности, ни к минус бесконечности, ни к нулю — никуда.

Рассмотрим теперь какой-нибудь дробный знаменатель между нулём и минус единичкой.

Тогда получим прогрессию:

И снова имеем чередование знаков! Но, в отличие от предыдущего примера, здесь уже прослеживается чёткая тенденция приближения членов к нулю.) Только в этот раз наши члены приближаются к нулю не строго сверху или снизу, а снова колеблясь. Попеременно принимая то положительные, то отрицательные значения. Но при этом их модули становятся всё ближе и ближе к заветному нолику.)

Такая геометрическая прогрессия называется бесконечно убывающей знакочередующейся.

Чем интересны эти два примера? А тем, что в обоих случаях имеет место чередование знаков! Такая фишка характерна только для прогрессий с отрицательным знаменателем, да.) Стало быть, если в каком-то задании вы увидите геометрическую прогрессию со знакочередующимися членами, то уже твёрдо будете знать, что её знаменатель на 100% отрицательный и не ошибётесь в знаке.)

Кстати, в случае отрицательного знаменателя знак первого члена совершенно не влияет на поведение самой прогрессии. С каким бы знаком первый член прогрессии ни был, в любом случае будет наблюдаться знакочередование членов. Весь вопрос лишь в том, на каких местах (чётные или нечётные) будут стоять члены с конкретными знаками.

Запоминаем:

Если знаменатель геометрической прогрессии отрицательный , то знаки членов прогрессии всегда чередуются.

При этом сами члены:

а) неограниченно возрастают по модулю, если q

Вот и всё. Все типовые случаи разобраны.)

В процессе разбора самых разных примеров геометрических прогрессий, я периодически употреблял слова: «стремится к нулю», «стремится к плюс бесконечности», «стремится к минус бесконечности»… Ничего страшного.) Эти речевые обороты (и конкретные примеры) — всего лишь начальное знакомство с поведением самых разных числовых последовательностей. На примере геометрической прогрессии.

Зачем нам вообще нужно знать поведение прогрессии? Какая разница, куда она там стремится? К нулю ли, к плюс бесконечности, к минус бесконечности… Нам-то что от этого?

Дело всё в том, что уже в ВУЗе, в курсе высшей математики, вам понадобится умение работать с самыми разными числовыми последовательностями (с любыми, а не только прогрессиями!) и умение представлять, как именно себя ведёт та или иная последовательность — возрастает ли она неограниченно, убывает ли, стремится ли к конкретному числу (причём не обязательно к нулю) или даже вообще ни к чему не стремится… Этой теме в курсе матанализа посвящён целый раздел — теория пределов. А чуть конкретнее — понятие предела числовой последовательности. Очень интересная тема! Имеет смысл поступить в институт и разобраться.)

Некоторые примеры из этого раздела (последовательности, имеющие предел) и в частности, бесконечно убывающая геометрическая прогрессия начинают осваиваться ещё в школе. Привыкаем.)

Более того, умение хорошо исследовать поведение последовательностей в дальнейшем здорово сыграет на руку и очень пригодится в исследовании функций. Самых разнообразных. А вот умение грамотно работать с функциями (вычислять производные, исследовать их по полной программе, строить их графики) уже резко повышает ваш математический уровень! Сомневаетесь? Не надо. Ещё вспомните мои слова.)

Посмотрим на геометрическую прогрессию в жизни?

В окружающей нас жизни с геометрической прогрессией мы сталкиваемся очень и очень часто. Даже сами того не подозревая.)

Например, различные микроорганизмы, которые окружают нас повсюду в огромных количествах и которых мы даже не видим без микроскопа, размножаются именно в геометрической прогрессии.

Скажем, одна бактерия размножается делением пополам, давая потомство в 2 бактерии. В свою очередь, каждая из них, размножаясь, тоже делится пополам, давая общее потомство в 4 бактерии. Следующее поколение даст уже 8 бактерий, потом 16 бактерий, 32, 64 и так далее. С каждым следующим поколением число бактерий удваивается. Типичный пример геометрической прогрессии.)

Также в геометрической прогрессии размножаются и некоторые насекомые — тля, мухи. И кролики иногда, кстати, тоже.)

Сами вы пока что ещё, конечно, юные. В школе учитесь, в банки не обращаетесь. А вот родители ваши — люди уже взрослые и самостоятельные. На работу ходят, денежки на хлеб насущный зарабатывают, а часть денег кладут в банк, делая сбережения.)

Скажем, ваш папа хочет поднакопить определённую денежную сумму на семейный отдых в Турции и положил в банк 50000 рублей под 10% годовых сроком на три года с ежегодной капитализацией процентов. Причём в течение всего этого срока делать со вкладом ничего нельзя. Нельзя ни пополнять вклад, ни снимать деньги со счёта. Какую прибыль он получит через эти три года?

Ну, во-первых, надо разобраться, что же такое 10% годовых. Это значит, что через год к первоначальной сумме вклада банком будут начислены 10%. От чего? Конечно же, от первоначальной суммы вклада.

Считаем размер счёта через год. Если первоначальная сумма вклада составляла 50000 рублей (т.е. 100%), то через год на счету будет сколько процентов? Правильно, 110%! От 50000 рублей.

Вот и считаем 110% от 50000 рублей:

50000·1,1 = 55000 рублей.

Надеюсь, вы понимаете, что найти 110% от величины означает помножить эту величину на число 1,1? Если не понимаете, почему это именно так, вспоминайте пятый и шестой классы. А именно – связь процентов с дробями и частями.)

Таким образом, прибавка за первый год составит 5000 рублей.

А сколько денег будет на счету через два года? 60000 рублей? К сожалению (а вернее, к счастью), всё не так просто. Весь фокус капитализации процентов состоит в том, что при каждом новом начислении процентов, эти самые проценты будут считаться уже от новой суммы! От той, которая уже лежит на счету в данный момент. А начисленные за предыдущий срок проценты прибавляются к изначальной сумме вклада и, таким образом, сами участвуют в начислении новых процентов! То есть, они становятся полноправной частью общего счёта. Или общего капитала. Отсюда и название — капитализация процентов.

Это в экономике. А в математике такие проценты называются сложными процентами. Или процентами от процентов.) Их фишка заключается в том, что при последовательном вычислении проценты каждый раз считаются от новой величины. А не от первоначальной…

Стало быть, для подсчёта суммы через два года, нам надо посчитать 110% от той суммы, которая будет на счету через год. То есть, уже от 55000 рублей.

Считаем 110% от 55000 рублей:

55000·1,1 = 60500 рублей.

Значит, процентная прибавка за второй год составит уже 5500 рублей, а за два года — 10500 рублей.

Теперь уже можно догадаться, что через три года сумма на счету будет составлять 110% от 60500 рублей. То есть снова 110% от предыдущей (прошлогодней) суммы.

60500·1,1 = 66550 рублей.

А теперь выстраиваем наши денежные суммы по годам в последовательность:

60500 = 55000·1,1 = (50000·1,1)·1,1;

66550 = 60500·1,1 = ((50000·1,1)·1,1)·1,1

Ну и как? Чем не геометрическая прогрессия? Первый член b₁ = 50000, а знаменатель q = 1,1. Каждый член больше предыдущего строго в 1,1 раза. Всё в строгом соответствии с определением.)

И сколько же дополнительных процентных бонусов «накапает» вашему папе, пока его 50000 рублей три года лежали на банковском счету?

66550 — 50000 = 16550 рублей

Негусто, конечно. Но это если изначальная сумма вклада — маленькая. А если побольше? Скажем, не 50, а 200 тысяч рублей? Тогда прибавка за три года составит уже 66200 рублей (если посчитать). Что уже очень неплохо.) А если вклад ещё больше? Вот то-то и оно…

Вывод: чем выше изначальный вклад, тем выгоднее становится капитализация процентов. Именно поэтому вклады с капитализацией процентов предоставляются банками на длительные сроки. Скажем, на пять лет.

Также в геометрической прогрессии любят распространяться всякие нехорошие болезни типа гриппа, кори и даже более страшных заболеваний (той же атипичной пневмонии в начале 2000-х или чумы в Средневековье). Отсюда и такие масштабы эпидемий, да…) А всё из-за того, что геометрическая прогрессия с целым положительным знаменателем (q>1) — штука, возрастающая очень быстро! Вспомните размножение бактерий: из одной бактерии получаются две, из двух — четыре, из четырёх — восемь и так далее… С распространением всякой заразы всё то же самое.)

Простейшие задачи по геометрической прогрессии.

Начнём, как всегда, с несложной задачки. Чисто на понимание смысла.

Итак, нам дана бесконечная геометрическая прогрессия, а известен второй член этой прогрессии:

Кроме того, нам ещё известен знаменатель прогрессии:

А найти нужно первый, третий и четвёртый члены этой прогрессии.

Вот и действуем. Записываем последовательность по условию задачки. Прямо в общем виде, где второй член — шестёрка:

А теперь приступаем к поискам. Начинаем, как всегда, с самого простого. Можно посчитать, например, третий член b₃? Можно! Мы же с вами уже знаем (прямо по смыслу геометрической прогрессии), что третий член (b₃) больше второго (b₂) в «q» раз!

Вот так. Третий член оказался с минусом. Неудивительно: наш знаменатель q — отрицательный. А плюс помножить на минус, будет, знамо дело, минус.)

Считаем теперь следующий, четвёртый член прогрессии:

Четвёртый член — снова с плюсом. Пятый член будет опять с минусом, шестой — с плюсом и так далее. Знаки — чередуются!

Так, третий и четвёртый члены нашли. Получилась вот такая последовательность:

Осталось теперь найти первый член b₁ по известному второму. Для этого шагаем уже в другую сторону, влево. Это значит, что в данном случае второй член прогрессии нам надо не помножить на знаменатель, а поделить.

Вот и всё.) Ответ к задачке будет такой:

Запоминаем: если нам известен хотя бы один член и знаменатель геометрической прогрессии, то мы всегда можем найти любой другой член этой прогрессии.

Следующая задачка, по традиции, из реального варианта ОГЭ:

2. Выписано несколько последовательных членов геометрической прогрессии:

…; 150; х; 6; 1,2; …

Найдите член прогрессии, обозначенный буквой х.

Ну и как? В этот раз ни первого члена нет, ни знаменателя q, задана просто последовательность чисел… Что-то знакомое уже, правда? Да! Похожая задачка уже разбиралась в первом уроке по арифметической прогрессии!

Вот и не пугаемся. Всё то же самое. Включаем голову и вспоминаем элементарный смысл геометрической прогрессии. Смотрим внимательно на нашу последовательность и соображаем, какие параметры геометрической прогрессии из трёх главных (первый член, знаменатель, номер члена) в ней спрятаны.

Номера членов? Номеров членов нету, да… Но зато есть четыре последовательных числа. Что означает это слово, объяснять на данном этапе смысла не вижу.) Есть ли в этой последовательности два соседних известных числа? Есть! Это 6 и 1,2. Значит, мы можем найти знаменатель прогрессии. Вот и берём число 1,2 и делим на предыдущее число. На шестёрку.

Всё. Дальше уже просто. Какое число будет предыдущим для икса? Сто пятьдесят! Значит, икс легко ищется простым умножением: 150 помножить на знаменатель геометрической прогрессии.

Как вы видите, всё довольно просто. Основная трудность состоит лишь в вычислениях. Особенно тяжко бывает в случае отрицательных и дробных знаменателей. Так что те, у кого проблемы, повторите арифметику! Как работать с дробями, как работать с отрицательными числами и так далее… Иначе здесь будете тормозить нещадно.

А теперь немного видоизменим задачку. Сейчас интересно станет! Уберём в ней последнее число 1,2. Вот такую задачку теперь решим:

3. Выписано несколько последовательных членов геометрической прогрессии:

…; 150; х; 6; …

Найдите член прогрессии, обозначенный буквой х.

Всё то же самое, только двух соседних известных членов прогрессии у нас теперь не стало. В этом и состоит основная проблема. Потому, что величину q через два соседних члена мы так просто определить уже не сможем. Есть у нас шанс справиться с задачей? Конечно!

Распишем неизвестный член « x» прямо по смыслу геометрической прогрессии! В общем виде.

Да-да! Прямо с неизвестным знаменателем!

С одной стороны, для икса мы можем записать вот такое соотношение:

С другой стороны, этот же самый икс мы имеем полное право расписать и через следующий член, через шестёрку! Поделив шестёрку на знаменатель.

Очевидно, теперь можно приравнять оба этих соотношения. Раз уж мы выражаем одну и ту же величину (икс), но двумя разными способами.

Умножая всё на q, упрощая, сокращая, получим уравнение:

Для q = +0,2 мы получим:

Что означает этот интересный факт? А то, что существует две прогрессии, удовлетворяющие условию задачи!

Обе — подходят.) Как вы думаете, из-за чего у нас произошло раздвоение ответов? Как раз из-за ликвидации конкретного члена прогрессии (1,2), идущего после шестёрки. А зная только предыдущий (n-1)-й и последующий (n+1)-й члены геометрической прогрессии, мы уже ничего не можем однозначно сказать про n-й член, стоящий между ними. Возможны два варианта — с плюсом и с минусом.

Но не беда. Как правило, в заданиях на геометрическую прогрессию имеется дополнительная информация, дающая однозначный ответ. Скажем, слова: «знакочередующаяся прогрессия» или «прогрессия с положительным знаменателем» и так далее… Именно эти слова и должны служить зацепкой, какой знак, плюс или минус, следует выбрать при оформлении окончательного ответа. Если же такой информации нет, то тогда — да, задача будет иметь два решения.)

А теперь решаем самостоятельно.

4. Определите, будет ли число 20 членом геометрической прогрессии:

4; 6; 9; …

5. Задана знакочередующаяся геометрическая прогрессия:

…; 5; x; 45; …

Найдите член прогрессии, обозначенный буквой x.

6. Найдите четвёртый положительный член геометрической прогрессии:

Поздравляю, если всё получилось!

Что-то не стыкуется? Где-то ответ двойной получился? Читаем внимательно условие задания!

Последняя задачка не выходит? Там ничего сложного.) Работаем прямо по смыслу геометрической прогрессии. Ну и картинку можно нарисовать. Это помогает.)

Как вы видите, всё элементарно. Если прогрессия — коротенькая. А если длинная? Или номер нужного члена очень большой? Хотелось бы, по аналогии с арифметической прогрессией, как-то получить удобную формулу, позволяющую легко находить любой член любой геометрической прогрессии по его номеру. Не помножая много-много раз на q. И такая формула есть!) Подробности — в следующем уроке.

Источник