Как доказать что тавтология
Методы доказательства тавтологии
Если каждая элементарная сумма, входящая в КНФ, содержит хотя бы одно высказывание вместе со своим отрицанием, то данная формула- тавтология.
В нашем примере так оно и есть, т.е. данная формула ─ тавтология
Таким образом, чтобы установить, к какому виду относится данная формула, нужно ее привести к ДНФ и КНФ.
1. Таблица истинности.
2. Приведение к КНФ.
3. Метод от противного.
Сущность 3-го метода заключается в том, что предполагается истинность противоположного утверждения, и на основании анализа формул мы получаем заключение о том, что она противоречит предположению. Это является доказательством того, что предположение ложно.
Пусть имеется формула (p
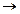
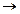
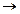
Предположим, что эта формула не является тавтологией. Это значит, что существует некоторый набор значений элементарных высказываний, при котором левая часть импликации истинна, а правая ложна. Пусть это: р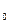
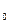
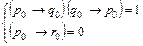
Из 3-его имеем р0 = 1. Тогда из 1 получим q0 = 1, а из 2 получим r0 = 1.
В результате r
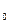
Мы пришли к противоречию, следовательно, наше предположение ложно и формула – тавтология.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Доказательство тавтологий
Этот алгоритм состоит в том, что переменным высказываниям, упорядоченным в набор, последовательно придаются значения И и Л и анализируются формулы, содержащие меньшее число переменных.
Пример: 















Метод обратных рассуждений
Очевидно, формула не является тавтологией, если она принимает значение Л хотя бы на одном наборе значений переменных. Этим обстоятельством можно воспользоваться для распознавания тавтологий сокращенным методом «обратного рассуждения». Этот метод заключается в поиске таких переменных, при которых формула оказывается ложной.
Пример: 
Используя известные законы логики высказываний, можно часть формулы или всю формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными. Равносильные преобразования используются для доказательства тавтологий, для приведения формул к заданному виду, для упрощения формул. При проведении равносильных преобразований каждый шаг основывается на использовании того или иного закона.
Пример: 
Доказательство тавтологий можно проводить с помощью правил вывода:
1. правило подстановки:_______________________________________________________________
2. правило заключения:_______________________________________________________________
Выводимая формула – __________________________________________________________
Вообще говоря, не все тождественно истинные формулы могут быть выведены из произвольного множества тавтологий. В то же время, строго доказано, что можно выбрать такую конечную совокупной исходных тавтологий (аксиом логики высказываний), из которой выводимы все тождественно истинные формулы.
Предложено много различных систем аксиом логики высказываний. Рассмотрим одну из них:
А1. ╞
А2. ╞
А3. ╞
Пример. Выведем тавтологию 
Рассмотрим еще одну систему аксиом:
А1. ╞
А2. ╞
А3. ╞
А4. ╞
А5. ╞
А6. ╞
А7. ╞
А8. ╞
А9. ╞
А10.╞
Пример. Выведем тавтологию из данной схемы аксиом.
Формализация процесса вывода имеет большое теоретическое значение и позволяет построить схему доказательства, которая может быть реализована на вычислительных машинах. Однако сложность аксиоматического подхода к выводу тавтологий заставляет искать и применять специальные правила, которые сокращают многократное применение основных правил вывода.
Производные правила вывода, как и рассмотренные правила подстановки и заключения, позволяют получать новые доказуемые формулы. Они получаются с помощью правил подстановки и заключения, а поэтому являются производными от них.
Правило сложного заключения.
Если формулы 


Если 


Если 

Правило исключения промежуточной посылки.
Если 


Правило перестановки посылок.
Если 

В содержательной математике утверждение «Из А следует В» обычно доказывается по следующей схеме. Предполагается, что А справедливо, посредством некоторой цепочки рассуждений устанавливается, что и В должно быть при этом справедливо, и заключается, что из А следует В. Кроме того, в рассуждениях может участвовать ряд дополнительных предположений. Формализацией этого способа доказательства является теорема о дедукции (для логики высказываний).
Теорема. Пусть Г: 


Пусть 




Случай 1. _______________________________________________________________________
Случай 2. _______________________________________________________________________
Случай 3. _______________________________________________________________________
Случай 4. _______________________________________________________________________
Пример. Докажем, что 
1. Высказывания, формулы, тавтологии
Определение. Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).
То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.
Пример. “Москва – столица России” – истинное высказывание.
“5 –четное число” – ложное высказывание.
“

“Студент второго курса” не высказывание (не является утверждением).
Высказывания бывают элементарные и составные.
Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с помощью элементарных высказываний.
Пример. “Число 22 четное” – элементарное высказывание.
“Число 22 четное и делится на 11” – составное высказывание.
Высказывания обозначают заглавными буквами латинского алфавита: 

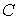
При фиксированном множестве букв 




Истинностные значения истина и ложь сокращенно обозначаются и, л или T, F, или 1,0. Мы будем использовать обозначения 1 и 0. В определенной интерпретации буквы принимают значения 1 или 0.
К высказываниям и буквам можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются Формулы (формы). Формулы становятся высказываниями при подстановке всех значений букв.
Таблицы истинности основных логических операций.
Более строго формула определяется так.
Определение. 1) Всякая буква есть формула.
2) Если 




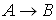
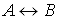
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).
В классической логике формулы принято заключать в круглые скобки, но в мы этого делать не будем. Для всякой формулы можно построить таблицу истинности.
Значение формулы 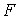




Часть формулы, которая сама является формулой, называется Подформулой данной формулы.
Определение. Формула называется Тавтологией, если она принимает только истинные значения при любых значениях букв.
Другими словами, тавтология – это тождественно истинная формула.
Установить, является ли формула тавтологией, можно:
– по таблице истинности,
– используя свойства логических операций.
Из курса дискретной математики известны основные логические эквивалентности (свойства логических операций), которые являются примерами тавтологий.
1. Коммутативность: 





4. Идемпотентность: 

5. Закон двойного отрицания: 
6. Закон исключения третьего: 
7. Закон противоречия: 
8. Законы де Моргана:


9. Свойства операций с логическими константами:




Здесь 

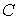
Примеры. 1. Доказать, что формула 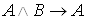
Доказательство. Допустим, что при некоторых значениях букв (то есть в некоторой интерпретации)
Приходим к противоречию, которое доказывает, что исходная формула – тавтология.
2. Доказать, что формула 
Доказательство. Эквиваленция истинна, если левая и правая части принимают одинаковые значения на некотором наборе значений букв.
Допустим, что при некоторых значениях букв
Следовательно, исходная формула – тавтология.
3. Доказать, что формула 
Доказательство. Допустим, что при некоторых значениях букв
Следовательно, исходная формула – тавтология.
Таким образом, тождественную истинность импликации удобно доказывать от противного, а тождественную истинность эквиваленции установлением равенства значений левой и правой части.
Теорема. Пусть формулы 
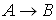

Доказательство. Пусть 



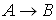






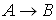







Теорема. Пусть формула 








Доказательство аналогично доказательству предыдущей теоремы.