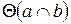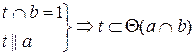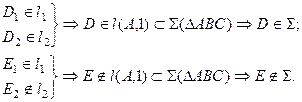Как доказать что точка принадлежит прямой

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

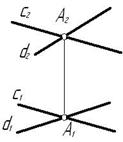
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Точка и прямая

Точка и прямая являются основными геометрическими фигурами на плоскости.

Определение точки и прямой в геометрии не вводят, эти понятия рассматриваются на интуитивно-понятийном уровне.

Точки обозначают прописными (заглавными, большими) латинскими буквами: A, B, C, D, …

Прямые обозначают одной строчной (маленькой) латинской буквой, например,

Прямая состоит из бесконечного множества точек и не имеет ни начала, ни конца. На рисунке изображают только часть прямой, но понимают, что она простирается в пространстве бесконечно далеко, неограниченно продолжаясь в обе стороны.

О точках, которые лежат на прямой, говорят, что они принадлежат этой прямой. Принадлежность отмечают знаком ∈. О точках вне прямой говорят, что они не принадлежат этой прямой. Знак «не принадлежит» — ∉.

Например, точка B принадлежит прямой a (пишут: B∈a),

точка F не принадлежит прямой a, (пишут: F∉a).

Основные свойства принадлежности точек и прямых на плоскости:

Каковы бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и притом только одну.

Прямые также обозначают двумя большими латинскими буквами, по названию точек, которые лежат на прямой.

— эту прямую можно назвать MK или MN или NK.

Две прямые могут пересекаться и не пересекаться. Если прямые не пересекаются, они не имеют общих точек. Если прямые пересекаются, они имеют одну общую точку. Знак пересечения — ∩.

Например, прямые a и b пересекаются в точке O

(пишут: a ∩ b=O).

Прямые c и d также пересекающиеся, хотя на рисунке нет их точки пересечения.

Прямые m и n не имеют общих точек.

Источник

Как доказать что точка принадлежит прямой

Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 28 точек, только одна точка С лежит на прямой АВ.

а) эпюр		б) модель
Рисунок 28. Взаимное расположение точки и прямой

В тех случаях, когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П₁, П₂ и П₃), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П₁, П₂ или П₃. Нап ример, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций (рис. 29 ).

Рисунок 29. Точка и прямая, расположенные в профильной плоскости уровня

Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении.

Зная это условие можно определить принадлежность точки К прямой АВ:

Источник

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник причем – точка ее пересечения со стороной – точка ее пересечения со стороной и – точка ее пересечения с продолжением стороны

Тогда выполняется равенство:

Как это запомнить? Сначала рисуем треугольник Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и причем на стороне должна лежать точка на стороне – точка и на продолжении – точка

Затем записываем равенство так, как будто «обходим» весь треугольник от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и – их тоже включаем в формулу.

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек и выполняется равенство: – то это означает, что точка лежит на отрезке Или, если нам удается доказать, что угол – развернутый, это и будет означать, что точки и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и – лежат на одной прямой.

Теорема Чевы

Пусть точки и лежат соответственно на сторонах и треугольника причем отрезки и пересекаются в одной точке. В этом случае выполняется равенство:

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Это значит, что по двум углам и то есть

Прямая пересекает две его стороны и продолжение третьей стороны

По теореме Менелая,

по углу и двум сторонам, отсюда

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Докажем, что — параллелограмм.

Тогда по углу и двум пропорциональным сторонам,

Это значит, что по углу и двум сторонам и

Получим, что в четырёхугольнике :

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

Тогда — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

Найдём из по теореме косинусов.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Проверим выполнение равенства

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Источник

Принадлежность прямой и точки плоскости

Рис. 3.2 Взаимное расположение прямых

Прямые в пространстве могут занимать относительно друг друга одно из трех положений:

1) быть параллельными;

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).

.

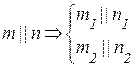
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

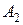
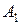
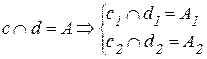
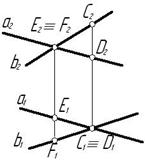
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная () и горизонтальная ()проекции этой точки должны находиться на одной линии связи.

.

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.

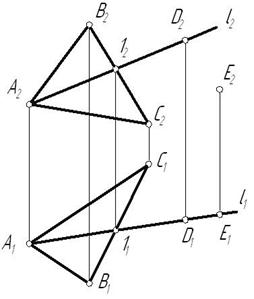
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).

Признак принадлежности точки и прямой плоскости:

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

На рис. 3.5 изображена плоскость 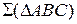и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.

На рис. 3.6 показана плоскость и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.

.

Источник