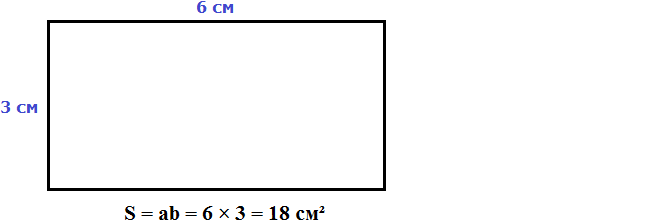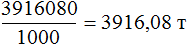Как найти площадь в чем измеряется

Площадь

Что такое площадь

Понятие площади фигур рассматривается одним из разделов математики — конкретно, геометрией. Результат решения задач с нахождением площади геометрических фигур может использоваться для решения математических задач, в быту, в производстве.

Площадь фигуры — численная характеристика, которая передает информацию о размере геометрической фигуры.

Фигура, в математическом мире определяемая как множество точек на плоскости, должна быть ограничена со всех сторон, чтобы иметь понятие площади. Если фигура располагается на одной плоскости, она не имеет объема, а только площадь.

В самом простом случае, площадь фигуры можно посчитать по количеству клеток, которые она занимает. Подобным способом можно легко посчитать площадь квадрата, прямоугольника или прямоугольного равнобедренного треугольника.

Площадь в геометрии обозначается знаком S, от английского square — площадь.

Как математическая характеристика, площадь имеет четыре характеристики:

Единицы измерения площади

Площадь фигуры может измеряться в разных единицах в зависимости от поверхности, на которой располагается. Основной системой измерения считается Международная система единиц СИ.

Площадь измеряется в единицах измерения в квадрате:

В Древней Руси употребляли такие величины, как квадратная верста, десятина, квадратный сажень.

В античных источниках единицей измерения площади были актус, арура, центурия, югер.

Формула нахождения площади в математике

Существует множество формул нахождения площади простых геометрических фигур, которые зависят, в основном, от количества углов, сторон и их соотношений.

Площадь прямоугольника

Прямоугольником является геометрическая фигура, все углы которой равны 90°. При этом таких углов должно быть, как минимум три, а четвертый будет равен 90° в силу закона о сумме углов четырехугольника в евклидовой геометрии.

Вычисление площади прямоугольника будет происходить через умножение сторон:

где a и b являются сторонами прямоугольника.

Площадь квадрата

Квадратом является прямоугольник с равными сторонами. Все его углы равны 90°. Площадь квадрата можно найти сразу двумя способами:

По длине стороны:

Через диагонали:

где a — длина сторон квадрата;

d — длина диагоналей квадрата.

Площадь круга

Кругом является часть плоскости, которая лежит внутри окружности. Круг не имеет ни одного угла, а точки его окружности находятся на равном удалении от центра.

Площадь круга можно найти двумя способами:

Через радиус:

где π — постоянная Пи, равна 3,14.

Радиус, упоминаемый в формуле, является линией или отрезком, соединяющим центр и любую из точек окружности.

Через диаметр:

где π — постоянная Пи, равна 3,14.

Диаметр является отрезком, соединяющим две точки окружности и проходящим через центр. Он включает в себя два противоположно направленных радиуса.

Площадь эллипса

Эллипс является частным случаем окружности. Он, так же, как и круг, не имеет ни одного угла, но при этом точки окружности находятся на разном удалении от центра.

Найти площадь эллипса можно только одним способом: через произведение длин большой и малой полуосей эллипса и числа пи.

Площадь эллипса находится через произведение длин большой и малой полуосей эллипса и числа пи:

Площадь параллелограмма

Параллелограмм является геометрической фигурой с 4 углами и 4 сторонами, однако он отличается от прямоугольника по строению. Его противолежащие стороны попарно параллельны, а углы равны зеркально противолежащим.

Частными случаями параллелограмма являются квадрат, прямоугольник и ромб.

Найти площадь параллелограмма можно тремя способами:

Через сторону и высоту:

где a — сторона, к которой проведена высота,

h — высота непосредственно.

Через две стороны и величину угла между ними:

Через диагонали и угол между ними:

S = 1 2 × d 1 × d 2 × sin y

где d 1 и d 2 — это диагонали параллелограмма,

y — угол между ними.

Площадь ромба

Ромб, как частный случай параллелограмма, имеет те же свойства, кроме того, что все его стороны равны.

Площадь ромба также можно найти тремя способами:

По длине стороны и высоте:

Формула площади ромба по стороне и высоте выглядит так же, как и площадь параллелограмма по таким же характеристикам, с условием, что все высоты ромба будут равны:

По длине стороны и углу:

Формула площади ромба через длину сторон и углу между ними похожа на соответствующую формулу площади параллелограмма с условием того, что стороны равны, а значит, их перемножение можно заменить квадратом величины стороны:

По длине его диагоналей:

Площадь трапеции

Трапеция отличается от всех предыдущих фигур тем, что только две ее стороны, боковые, могут быть равны между собой. При этом они не параллельны. Две другие стороны параллельны, но не равны. Сумма углов трапеции равна 360°.

Площадь трапеции можно найти двумя способами:

По формуле Герона:

По длине основ и высоте:

Площадь треугольника

Треугольник является геометрической фигурой с тремя сторонами и суммой углов, равной 180°. По величине углов треугольники делятся на острые, тупые и прямоугольные. По числу равных сторон треугольники делятся на разносторонние, равносторонние и равнобедренные.

Площадь треугольника можно найти множеством способов:

По гипотенузе и острому углу:

a — любой из прилежащих острых углов.

Через сторону и высоту:

Через три стороны:

где р — полупериметр.

Через две стороны и угол между ними:

S = 1 2 × a × b × sin y

Через три стороны и радиус описанной окружности:

Через три стороны и радиус вписанной окружности:

где р — полупериметр.

Пояснения на примерах

Стены класса равны 7 и 5 метрам. Чему будет равна площадь пола в данной комнате?

Решение: S = 7 × 5 = 35

Ткань летучего змея порвалась. Вася решил сделать новую форму. Он посчитал, что длина жердей летучего змея равна 15 и 23 см. Форму какой площади нужно взять Васе с учетом того, что для припусков для пришивания нужно взять еще 2 см?

Равнобедренный треугольник имеет основание 4 дм и высоту 7 дм. Сколько будет его площадь?

Источник

Как найти площадь фигуры

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах измерения длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.

S = &pi × d 2 : 4;, где d — это диаметр.

S = L 2 ​ : (4 × π), где L — это длина окружности.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Треугольник

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, соединенных тремя отрезками. Эти три точки принято называть вершинами, а отрезки — сторонами. Рассчитать площадь треугольника можно несколькими способами по исходными данным, давайте их рассмотрим.

1. Если известна сторона и высота.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

2. Если известны две стороны и синус угла.

S = 0,5 × a × b * sinα, где a и b — две стороны, sinα — синус угла между ними.

3. Если есть радиус описанной окружности.

S = (a × b × с) : (4 × R), где a, b и с — стороны треугольника, а R — радиус описанной окружности.

4. Если есть радиус вписанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Прямоугольник

Прямоугольник — это параллелограмм, у которого все углы прямые. Узнать площадь прямоугольника помогут следующие формулы:

S = a × b, где a, b — длина и ширина прямоугольника.

Диагональ — это отрезок, который соединяет вершины противоположных углов. Она есть во всех фигурах, число вершин которых больше трех.

S = 0,5 × d 2 × 𝑠𝑖𝑛(𝑎), где d — диагональ, α — угол между диагоналями.

Квадрат

Квадрат — это тот же прямоугольник, но при условии, что все его стороны равны. Найти его площадь легко:

S = d 2 : 2, где d — диагональ.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.

S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм, у которого все стороны равны.

Расскажем про общие формулы расчета площади этих фигур.

S = a × h, где a — сторона, h — высота.

S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.

Для ромба: S = 0,5 × (d₁ × d₂), где d₁, d₂ — две диагонали. Для параллелограмма: S = 0,5 × (d₁ × d₂) × sinβ, где β — угол между диагоналями.

Источник

Периметр, площадь и объём

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

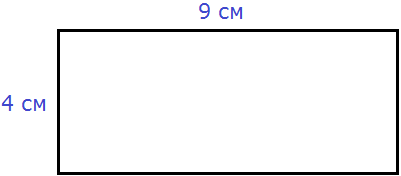
Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

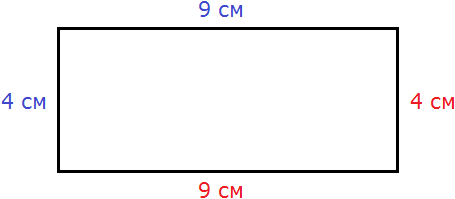
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters ). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

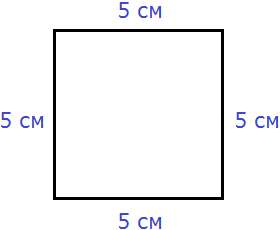
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

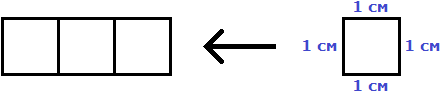
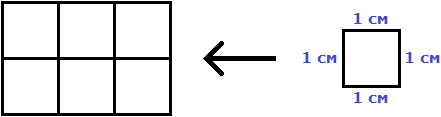
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

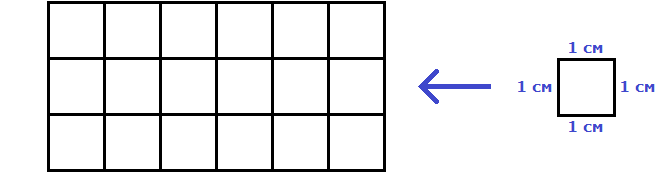
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

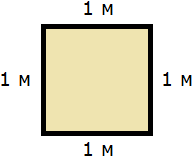
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

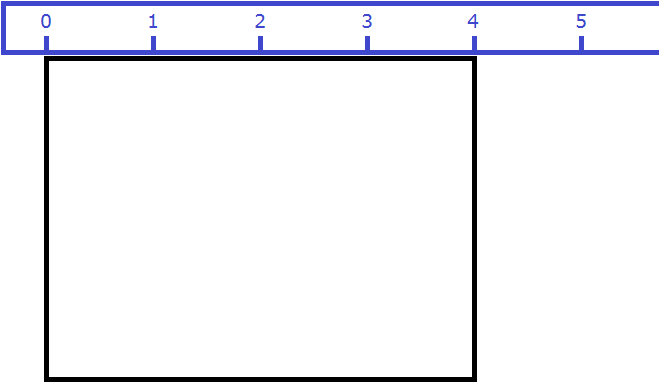
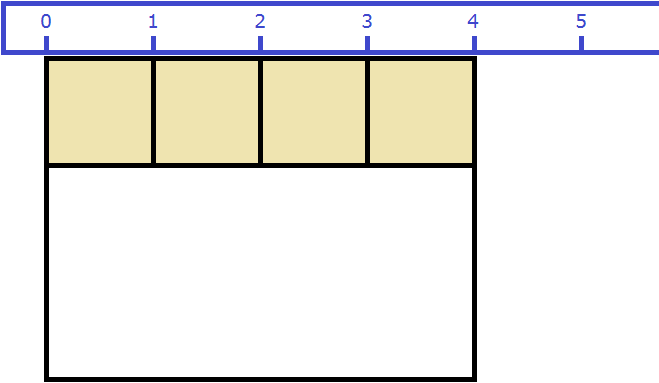
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

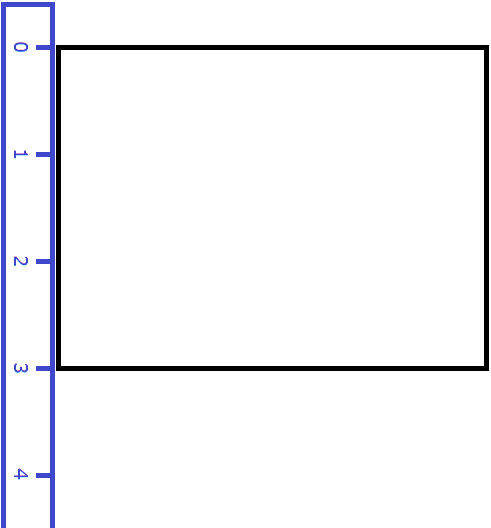
Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).

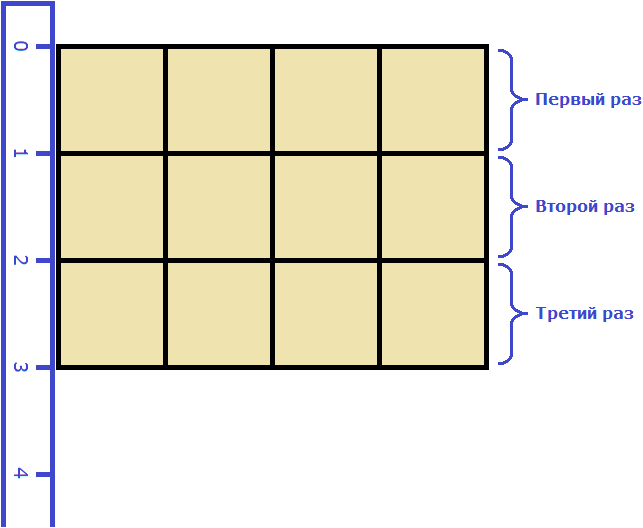
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

Площадь квадрата

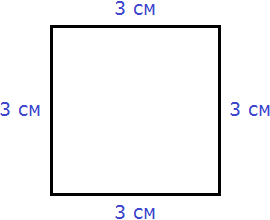
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

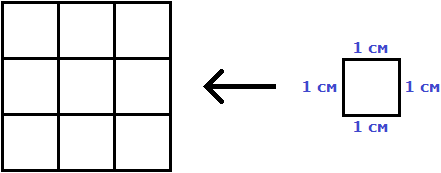
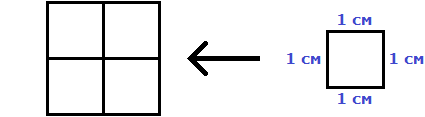
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

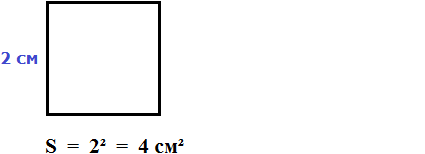
Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

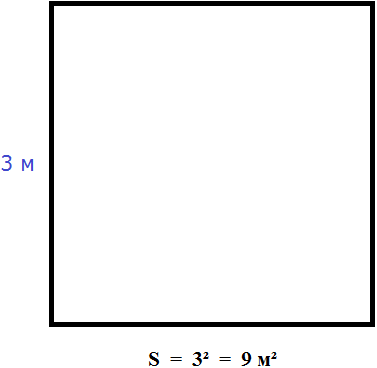
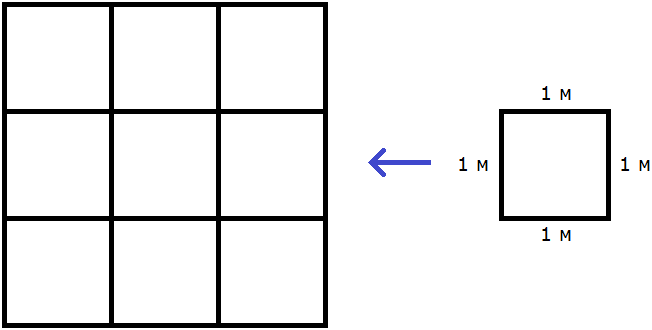
Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

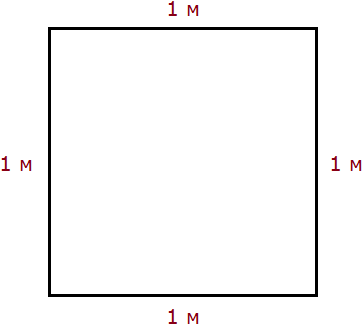
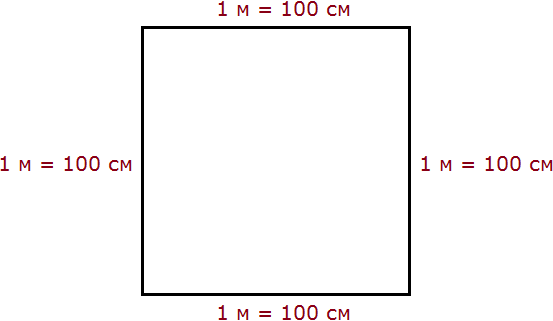
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 100 2 = 10 000 см 2

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м 2 = 10 000 см 2

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

Например, переведём 100 000 см 2 в квадратные метры. Рассуждать в этом случае можно так: « если 10 000 см 2 это один квадратный метр, то сколько раз 100 000 см 2 будут содержать по 10 000 см 2 »

100 000 см 2 : 10 000 см 2 = 10 м 2

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км 2 в квадратные метры.

S = 1000 2 = 1 000 000 м 2

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км 2 = 1 000 000 м 2

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км 2 в квадратные метры. Умножим 2 км 2 на 1 000 000

2 км 2 × 1 000 000 = 2 000 000 м 2

Например, переведём 3 500 000 м 2 в квадратные километры. Рассуждать в этом случае можно так: « если 1 000 000 м 2 это один квадратный километр, то сколько раз 3 500 000 м 2 будут содержать по 1 000 000 м 2 »

3 500 000 м 2 : 1 000 000 м 2 = 3,5 км 2

Пример 2. Выразить 7 м 2 в квадратных сантиметрах.

Умножим 7 м 2 на 10 000

7 м 2 = 7 м 2 × 10 000 = 70 000 см 2

Пример 3. Выразить 5 м 2 13 см 2 в квадратных сантиметрах.

5 м 2 13 см 2 = 5 м 2 × 10 000 + 13 см 2 = 50 013 см 2

Пример 4. Выразить 550 000 см 2 в квадратных метрах.

550 000 см 2 : 10 000 см 2 = 55 м 2

Пример 5. Выразить 7 км 2 в квадратных метрах.

Умножим 7 км 2 на 1 000 000

7 км 2 × 1 000 000 = 7 000 000 м 2

Пример 6. Выразить 8 500 000 м 2 в квадратных километрах.

8 500 000 м 2 × 1 000 000 м 2 = 8,5 км 2

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам ( 100 м 2 ). В виду частого распространения такой площади ( 100 м 2 ) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м 2 каждый, то есть:

3 а = 100 м 2 × 3 = 300 м 2

10 соток = 1000 м 2

20 га = 10 000 м 2 × 20 = 200 000 м 2

Прямоугольный параллелепипед и куб

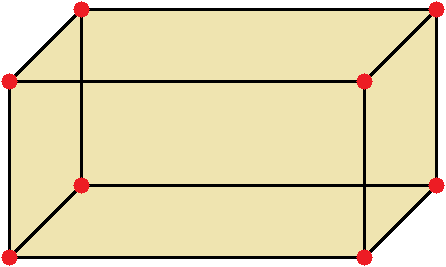
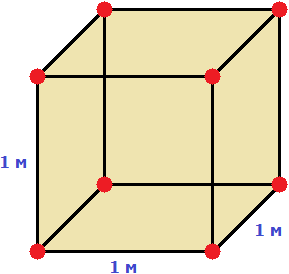
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

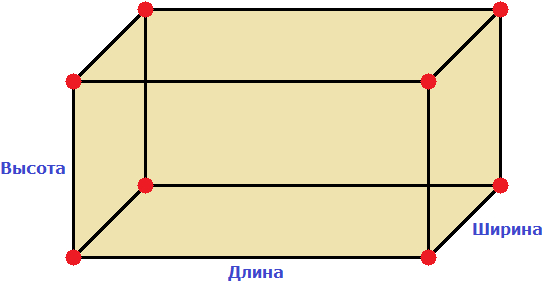
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

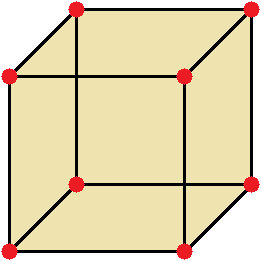
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.

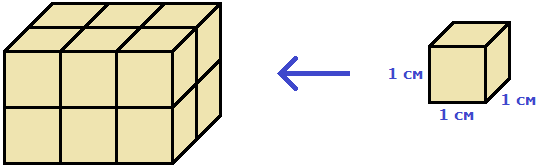
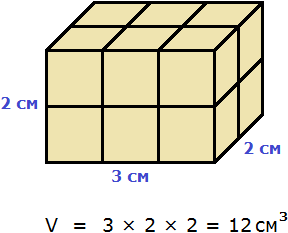
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см 3 ). Тогда объём V рассмотренного нами параллелепипеда равен 12 см 3

V = 12 см 3

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

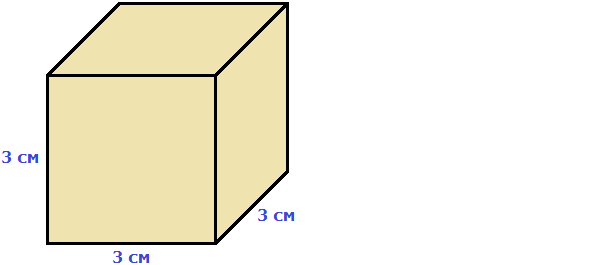
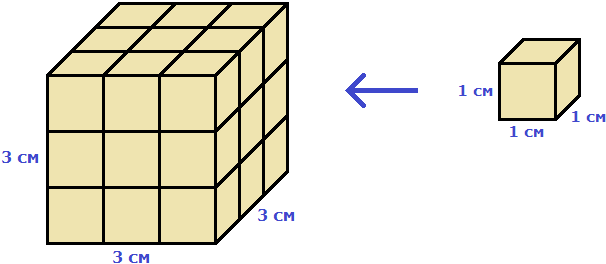
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

Таким образом, объём куба вычисляется по следующему правилу:

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах ( м 3 ). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах ( дм 3 ).

Другое название одного кубического дециметра – один литр.

1 дм 3 = 1 литр

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

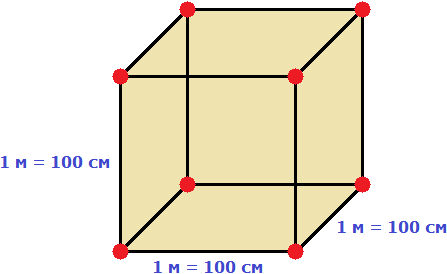
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 100 3 = 1 000 000 см 3

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м 3 = 1 000 000 см 3

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

Например, переведём 300 000 000 см 3 в кубические метры. Рассуждать в этом случае можно так: « если 1 000 000 см 3 это один кубический метр, то сколько раз 300 000 000 см 3 будут содержать по 1 000 000 см 3 »

300 000 000 см 3 : 1 000 000 см 3 = 300 м 3

Пример 2. Выразить 3 м 3 в кубических сантиметрах.

Умножим 3 м 3 на 1 000 000

3 м 3 × 1 000 000 = 3 000 000 см 3

Пример 3. Выразить 60 000 000 см 3 в кубических метрах.

60 000 000 см 3 : 1 000 000 см 3 = 60 м 3

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм 3

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм 3

Теперь переведём эти 6000 дм 3 в кубические метры.

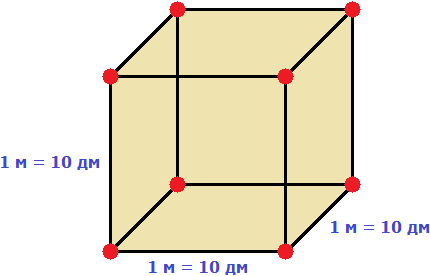
Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1 000 дм 3

V = 10 3 = 1000 дм 3

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм 3 содержит по 1 000 дм 3

6 000 дм 3 : 1 000 дм 3 = 6 м 3

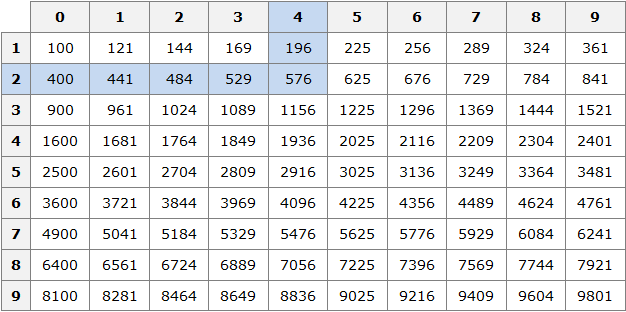
Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

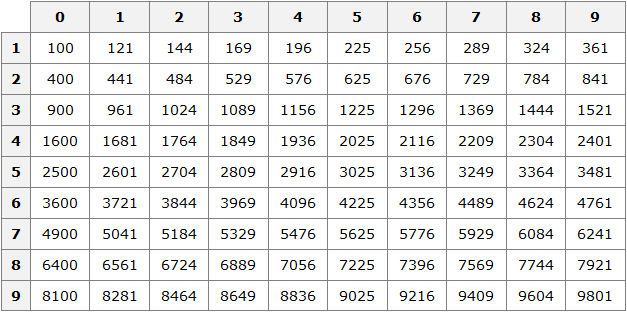
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

24 2 = 576

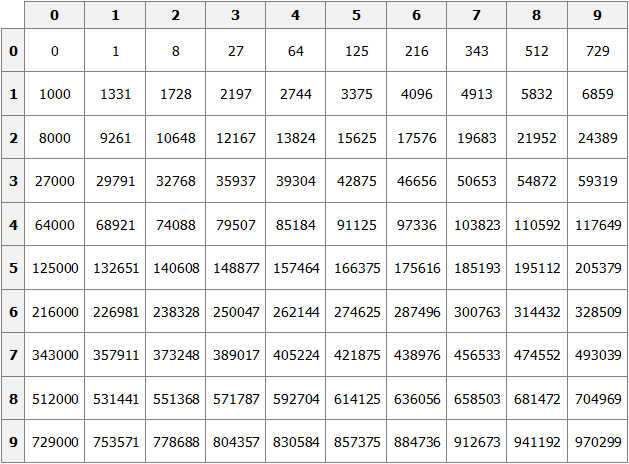
Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

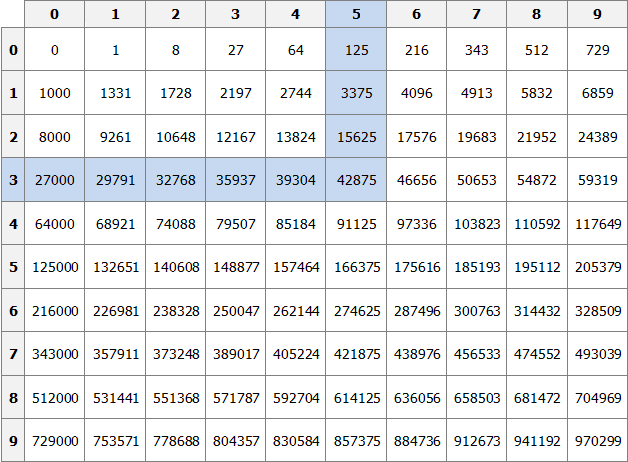
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

35 3 = 42875

Задания для самостоятельного решения

Решение

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Решение

Решение

Ответ: ширина прямоугольника составляет 2 см.

Решение

S = a 2
a = 8
S = 8 2 = 64 см 2
Ответ: площадь квадрата со стороной 8 см равна 64 см 2

Решение

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см 3

Решение

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

Ответ: пшеницей засеяно 12 га.

Решение

a = 42 м
b = 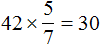м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м 3

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм 3

35 525 л = 35 525 дм 3

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм 3 : 1000 дм 3 = 35,525 м 3

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

9 thoughts on “Периметр, площадь и объём”

Ура. Вы снова в деле. Всегда будем рады новым урокам.

Благодарю. Все четко, последовательно, без воды. Пожалуйста не останавливайтесь! Желаю успехов в ваших проектах.

Продовжуйте працювати! Спасибі, що ви випукаєте нові уроки. Чекаю на нові уроки із захопленням.

Продовжуйте працювати! Спасибі, що ви випукаєте нові уроки, я чекаю на них із захопленням.

Источник