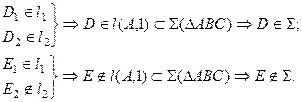Как обозначается то что точка а принадлежит плоскости а

Как доказать что точка принадлежит плоскости

Для определения принадлежности точки и прямой плоскости, расположенной в пространстве, следует руководствоваться следующими ‘ положениями:

· точка принадлежит плоскости, если через нее можно провести линию, лежащую в плоскости;

· прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки;

· прямая принадлежит плоскости, если она проходит через точку данной плоскости параллельно прямой, принадлежащей этой плоскости.

Через одну точку на плоскости можно провести бесконечное множество линий. Это могут быть произвольные линии и линии, занимающие особое положение по отношению к плоскостям проекций П₁ П₂, П₃.Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно горизонтальной плоскости проекций, называется горизонталью плоскости.

Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно фронтальной плоскости проекций, называется фронталью плоскости.

Горизонталь и фронталь являются линиями уровня.

Горизонталь плоскости следует начинать строить с фронтальной проекции, т.к. она параллельна оси x, горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

А так как все горизонтали плоскости параллельны между собой, можно считать горизонтальный след плоскости нулевой горизонталью (рис. 5.8).

К линии уровня относится и профильная прямая, лежащая в заданной плоскости и параллельная П₃.

К главным линиям особого положения в плоскости, кроме линии уровня, относятся линии наибольшего наклонаплоскости к плоскости проекций.

Определение угла наклона плоскости

К плоскостям проекций

Плоскость общего положения, расположенная в пространстве
произвольно, наклонена к плоскостям проекций. Для определения величины двухгранного угла наклона заданной плоскости к какой-либо
плоскости проекции используются линии наибольшего наклона плоскости к плоскости проекций: к П₁ – линия ската, к П₂ – линия наибольшего наклона плоскости к плоскости П₂.

Линии наибольшего наклона плоскости – это прямые, образующие с плоскостью проекций наибольший угол, проводятся в плоскости перпендикулярно к соответствующей линии уровня. Линии наибольшего наклона и ее соответствующая проекция образуют линейный угол, которым измеряется величина двухгранного угла, составленное данной плоскостью и плоскостью проекций (рис. 5.10).

Последнее изменение этой страницы: 2016-12-10; Нарушение авторского права страницы

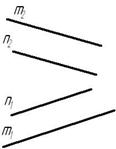
Рис. 3.2 Взаимное расположение прямых

Прямые в пространстве могут занимать относительно друг друга одно из трех положений:

1) быть параллельными;

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).

.

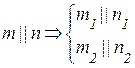
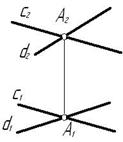
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

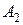
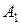
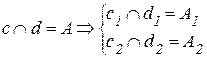
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная () и горизонтальная ()проекции этой точки должны находиться на одной линии связи.

.

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.

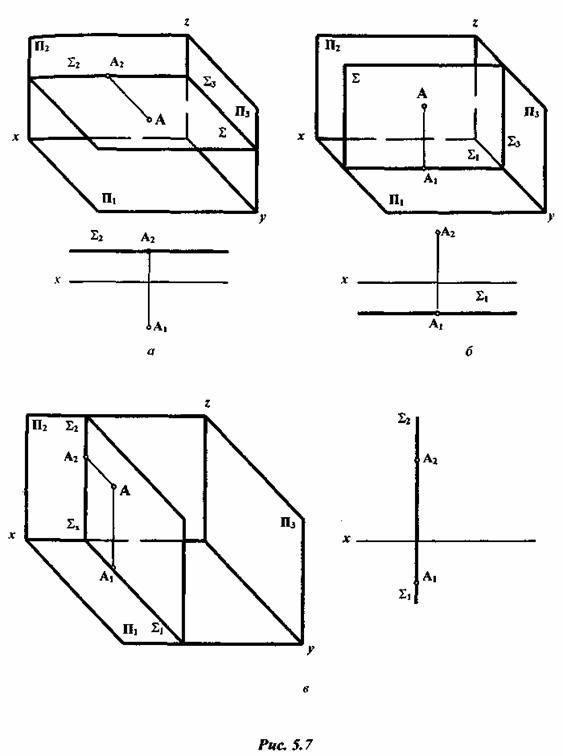
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).

Признак принадлежности точки и прямой плоскости:

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

На рис. 3.5 изображена плоскость и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.

На рис. 3.6 показана плоскость 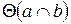и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.

.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 – | 7538 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Принадлежность точки плоскости на комплексном чертеже определяется согласно аксиоме инцидентности или отношения принадлежности между элементами евклидова пространства, которая гласит: – если точка E принадлежит прямой k, а прямая k принадлежит плоскости α, то точка E принадлежит плоскости α: E ∈ k ∧ k ∈ α ⇒ E ∈ α.

Задача на принадлежность точки плоскости может быть выражена следующим образом: – заключить точку E(E`, E») в; – провести через точку E(E`, E») плоскость α общего положения

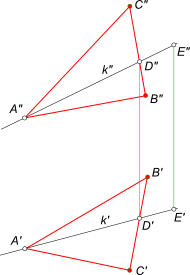
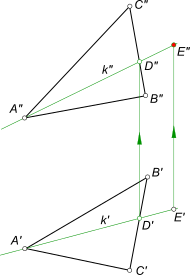
Положение плоскости α в пространстве определяется тремя точками – вершинами ΔABC. Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки A и D принадлежат этой плоскости. Проведя прямую в плоскости через точку E

доказываем тем самым ее принадлежность заданной плоскости. Заключить точку M в плоскость α заданную параллельными прямыми a и b

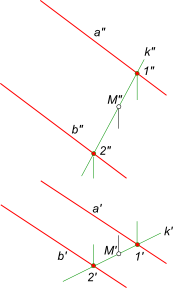
Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки 1 и 2 принадлежат этой плоскости. Построение искомой плоскости α: – проводим прямую через точку M; – через точки 1 и 2 взятые на прямой k проводим взаимно параллельные прямые a и b соответственно.

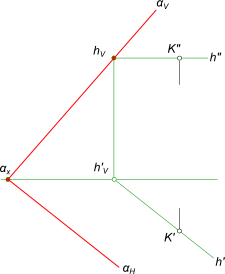
Через точку M провести плоскость α заданную следами

Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой h, которая, в то же время, принадлежит плоскости α и является ее горизонталью. Построение искомой плоскости α: – проводим прямую h (горизонталь искомой плоскости) через точку K; – проводим горизонтальный след α_H // h` ⇒ α_x; – через точки α_x и h_V проводим фронтальный след α_V.

Источник

Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой этой плоскости.

Прямая принадлежит плоскости, если две ее точки принадлежат плоскости.

Эти два вполне очевидных предложения часто называют условиями принадлежности точки и прямой плоскости.

На рис. 3.6 плоскость общего положения задана треугольником АВС. Точки А, В, С принадлежат этой плоскости, так как являются вершинами треугольника из этой плоскости. Прямые (АВ), (ВС), (АС) принадлежат плоскости, так как по две их точки принадлежат плоскости. Точка N принадлежит (AC), D принадлежит (AB), E принадлежит (CD) и, значит, точки N и E принадлежат плоскости (DABC), тогда прямая (NE) принадлежит плоскости (DABC).

Если задана одна проекция точки L, например L₂, и известно, что точка L принадлежит плоскости (DABC), то для нахождения второй проекции L₁ последовательно находим (A₂L₂), K₂, (A₁K₁), L₁.

Если условие принадлежности точки плоскости нарушено, то точка не принадлежит плоскости. На рис. 3.6 точка R не принадлежит плоскости (DABC), так как R₂ принадлежит (F₂K₂), а R₁ не принадлежит (A₁K₁).

На рис. 3.7 приведен комплексный чертеж горизонтально проецирующей плоскости (DCDE). Точки K и P принадлежат этой плоскости, так как P₁ и K₁ принадлежат прямой (D₁C₁), являющейся горизонтальной проекцией плоскости (DCDE). Точка N не принадлежит плоскости, так как N₁ не принадлежит (D₁C₁).

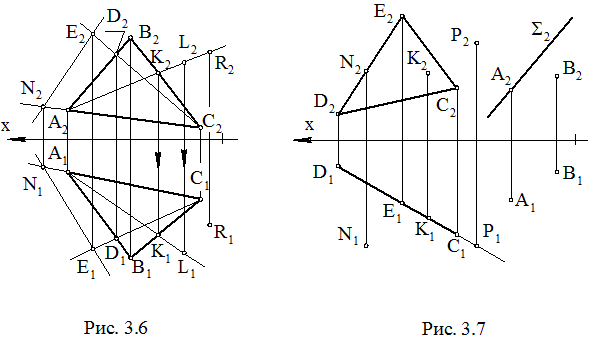
Все точки плоскости (DCDE) проецируются на П₁ в прямую (D₁C₁). Это следует из того, что плоскость (DCDE) ^ П₁. В этом же можно убедиться, если проделать для точки P (или любой другой точки) построения, которые были сделаны для точки L (рис. 3.6). Точка P₁ попадет на прямую (D₁C₁). Таким образом, для того, чтобы определить принадлежность точки горизонтально проецирующей плоскости, фронтальная проекция (DC₂D₂E₂) не нужна. Поэтому в дальнейшем проецирующие плоскости будут задаваться только одной проекцией (прямой линией). На рис. 3.7 показана фронтально проецирующая плоскость S, заданная фронтальной проекцией S₂, а также точки A Î S и B Ï S.

Взаимное положение точки и плоскости сводится к принадлежности или не принадлежности точки плоскости.

При решении многих задач приходится строить линии уровня, принадлежащие плоскостям общего и частного положения. На рис. 3.8 показаны горизонталь h и фронталь f, принадлежащие плоскости общего положения (DABC). Фронтальная проекция h₂ параллельна оси x, поэтому прямая h – горизонталь. Точки 1 и 2 прямой h принадлежат плоскости, поэтому прямая h принадлежит плоскости. Таким образом, прямая h – это горизонталь плоскости (DABC). Обычно порядок построения такой: h₂; 1₂, 2₂; 1₁, 2₁; (1₁2₁) = h₁. Фронталь f проведена через точку A. Порядок построения: f₁ // x, A₁Î f₁; 3₁, 3₂; (A₂3₂) = f₂.

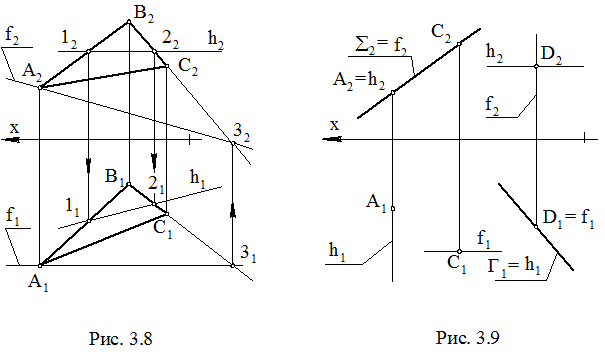На рис. 3.9 показаны проекции горизонтали и фронтали для фронтально проецирующей плоскости S и горизонтально проецирующей плоскости Г. В плоскости S горизонталь является фронтально проецирующей прямой и проходит через точку A (попытайтесь представить горизонталь как линию пересечения S и плоскости, проходящей через точку A параллельно П₁). Фронталь проходит через точку С. В плоскости Г горизонталь и фронталь проведены через одну точку D. Фронталь является горизонтально проецирующей прямой.

Из рассмотренных выше построений следует, что линию уровня в плоскости можно провести через любую точку этой плоскости.

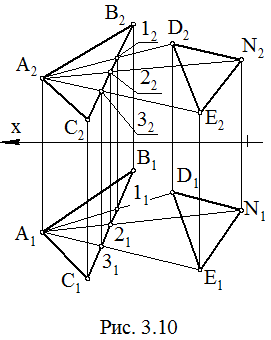
Совпадение плоскостей можно трактовать как принадлежность одной плоскости другой. Если три точки одной плоскости принадлежат другой плоскости, то эти плоскости совпадают. Упомянутые три точки не должны лежать на одной прямой. На рис. 3.10 плоскость (DDNE) совпадает с плоскостью S(DABC), так как точки D, N, E принадлежат плоскости S(DABC).

Обратим внимание на то, что плоскость S, заданная DABC, теперь может быть задана DDNE. Любая плоскость может быть задана линиями уровня. Для этого необходимо через точку плоскости S(DABC) (например, через точку А) провести в плоскости горизонталь и фронталь, которые и будут задавать плоскость S (на рис. 3.10 построения не показаны). Последовательность построения горизонтали: h₂ // x (A₂ Î h₂); K₂ = h₂ Ç B₂C₂; K₁ Î B₁C₁ (K₂K₁ ^ x); A₁K₁ = h₁. Последовательность построения фронтали: f₁ // x (A₁ Î f₁); L₁ = f₁ Ç B₁C₁; L₂ Î B₂C₂ (L₁L₂ ^ x); A₂L₂ = f₂. Можно записать S(DABC) = S(h, f).

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой этой плоскости.

Прямая принадлежит плоскости, если две ее точки принадлежат плоскости.

Эти два вполне очевидных предложения часто называют условиями принадлежности точки и прямой плоскости.

На рис. 3.6 плоскость общего положения задана треугольником АВС. Точки А, В, С принадлежат этой плоскости, так как являются вершинами треугольника из этой плоскости. Прямые (АВ), (ВС), (АС) принадлежат плоскости, так как по две их точки принадлежат плоскости. Точка N принадлежит (AC), D принадлежит (AB), E принадлежит (CD) и, значит, точки N и E принадлежат плоскости (DABC), тогда прямая (NE) принадлежит плоскости (DABC).

Если задана одна проекция точки L, например L₂, и известно, что точка L принадлежит плоскости (DABC), то для нахождения второй проекции L₁ последовательно находим (A₂L₂), K₂, (A₁K₁), L₁.

Если условие принадлежности точки плоскости нарушено, то точка не принадлежит плоскости. На рис. 3.6 точка R не принадлежит плоскости (DABC), так как R₂ принадлежит (F₂K₂), а R₁ не принадлежит (A₁K₁).

На рис. 3.7 приведен комплексный чертеж горизонтально проецирующей плоскости (DCDE). Точки K и P принадлежат этой плоскости, так как P₁ и K₁ принадлежат прямой (D₁C₁), являющейся горизонтальной проекцией плоскости (DCDE). Точка N не принадлежит плоскости, так как N₁ не принадлежит (D₁C₁).

Все точки плоскости (DCDE) проецируются на П₁ в прямую (D₁C₁). Это следует из того, что плоскость (DCDE) ^ П₁. В этом же можно убедиться, если проделать для точки P (или любой другой точки) построения, которые были сделаны для точки L (рис. 3.6). Точка P₁ попадет на прямую (D₁C₁). Таким образом, для того, чтобы определить принадлежность точки горизонтально проецирующей плоскости, фронтальная проекция (DC₂D₂E₂) не нужна. Поэтому в дальнейшем проецирующие плоскости будут задаваться только одной проекцией (прямой линией). На рис. 3.7 показана фронтально проецирующая плоскость S, заданная фронтальной проекцией S₂, а также точки A Î S и B Ï S.

Взаимное положение точки и плоскости сводится к принадлежности или не принадлежности точки плоскости.

При решении многих задач приходится строить линии уровня, принадлежащие плоскостям общего и частного положения. На рис. 3.8 показаны горизонталь h и фронталь f, принадлежащие плоскости общего положения (DABC). Фронтальная проекция h₂ параллельна оси x, поэтому прямая h – горизонталь. Точки 1 и 2 прямой h принадлежат плоскости, поэтому прямая h принадлежит плоскости. Таким образом, прямая h – это горизонталь плоскости (DABC). Обычно порядок построения такой: h₂; 1₂, 2₂; 1₁, 2₁; (1₁2₁) = h₁. Фронталь f проведена через точку A. Порядок построения: f₁ // x, A₁Î f₁; 3₁, 3₂; (A₂3₂) = f₂.

На рис. 3.9 показаны проекции горизонтали и фронтали для фронтально проецирующей плоскости S и горизонтально проецирующей плоскости Г. В плоскости S горизонталь является фронтально проецирующей прямой и проходит через точку A (попытайтесь представить горизонталь как линию пересечения S и плоскости, проходящей через точку A параллельно П₁). Фронталь проходит через точку С. В плоскости Г горизонталь и фронталь проведены через одну точку D. Фронталь является горизонтально проецирующей прямой.

Из рассмотренных выше построений следует, что линию уровня в плоскости можно провести через любую точку этой плоскости.

Совпадение плоскостей можно трактовать как принадлежность одной плоскости другой. Если три точки одной плоскости принадлежат другой плоскости, то эти плоскости совпадают. Упомянутые три точки не должны лежать на одной прямой. На рис. 3.10 плоскость (DDNE) совпадает с плоскостью S(DABC), так как точки D, N, E принадлежат плоскости S(DABC).

Обратим внимание на то, что плоскость S, заданная DABC, теперь может быть задана DDNE. Любая плоскость может быть задана линиями уровня. Для этого необходимо через точку плоскости S(DABC) (например, через точку А) провести в плоскости горизонталь и фронталь, которые и будут задавать плоскость S (на рис. 3.10 построения не показаны). Последовательность построения горизонтали: h₂ // x (A₂ Î h₂); K₂ = h₂ Ç B₂C₂; K₁ Î B₁C₁ (K₂K₁ ^ x); A₁K₁ = h₁. Последовательность построения фронтали: f₁ // x (A₁ Î f₁); L₁ = f₁ Ç B₁C₁; L₂ Î B₂C₂ (L₁L₂ ^ x); A₂L₂ = f₂. Можно записать S(DABC) = S(h, f).

ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА

В курсе начертательной геометрии под преобразованием комплексного чертежа фигуры обычно понимается его изменение, вызванное перемещением фигуры в пространстве, или введением новых плоскостей проекций, или использованием других видов проецирования. Применение различных методов (способов) преобразования комплексного чертежа упрощает решение многих задач.

4.1. Метод замены плоскостей проекций

Метод замены плоскостей проекций состоит в том, что вместо одной из плоскостей проекций вводится новая плоскость, перпендикулярная к другой плоскости проекций. На рис. 4.1 показана пространственная схема получения комплексного чертежа точки А в системе (П₁П₂). Точки А₁ и А₂ – горизонтальная и фронтальная проекции точки А, АА₁А_xА₂ – прямоугольник, плоскость которого перпендикулярна оси x (рис. 2.3).

Новая плоскость П₄ перпендикулярна П₁. При проецировании точки А на П₄ получим новую проекцию А₄, фигура АА₁А₁₄А₄ – прямоугольник, плоскость которого перпендикулярна новой оси x₁₄ = П₄ Ç П₁. Для получения комплексного чертежа будем рассматривать фигуры, расположенные в плоскостях проекций. Поворотом вокруг оси x₁₄ совместим П₄ с П₁, затем поворотом вокруг оси x совместим П₁ (и П₄) с П₂ (на рис. 4.1 направления движения плоскостей П₄ и П₁ показаны штриховыми линиями со стрелками). Полученный чертеж приведен на рис. 4.2. Прямые углы на рис. 4.1, 4.2 помечены дугой с точкой, равные отрезки помечены двумя штрихами (противоположные стороны прямоугольников на рис. 4.1). От комплексного чертежа точки А в системе (П₁П₂) перешли к комплексному чертежу точки А в системе (П₁П₄), заменили плоскость П₂ на плоскость П₄, заменили А₂ на А₄.

На основе этих построений сформулируем правило замены плоскостей проекций (правило получения новой проекции). Через незаменяемую проекцию проводим новую линию проекционной связи перпендикулярно новой оси, затем от новой оси по линии проекционной связи откладываем отрезок, длина которого равна расстоянию от заменяемой проекции до старой оси, полученная при этом точка и есть новая проекция. Направление новой оси будем брать произвольно. Новое начало координат указывать не будем.

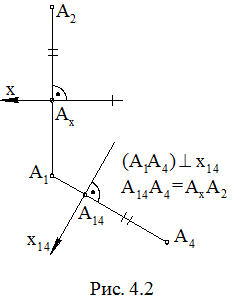
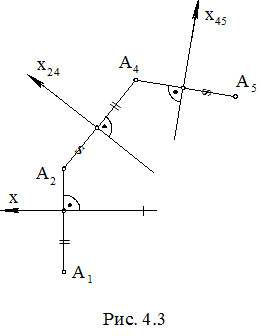
На рис. 4.3 показан переход от комплексного чертежа в системе (П₁П₂) к комплексному чертежу в системе (П₂П₄), а затем еще один переход к комплексному чертежу в системе (П₄П₅). Вместо плоскости П₁ введена плоскость П₄, перпендикулярная П₂, затем вместо П₂ введена плоскость П₅, перпендикулярная П₄. Используя правило замены плоскостей проекций, можно выполнить любое количество замен плоскостей проекций.

Источник