Как обозначается то что точка с является пересечением прямых а и б

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Обозначения и символика

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Источник

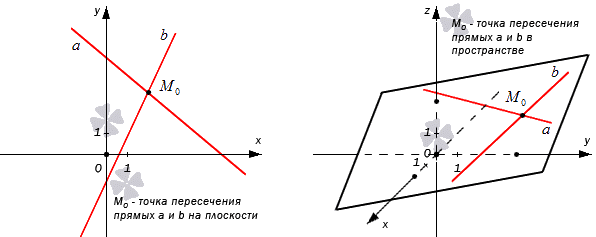
Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

Точка пересечения двух прямых – определение

Необходимо дать определение точкам пересечения двух прямых.

Определение точки пересечения прямых звучит так:

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

Рассмотрим на рисунке, приведенном ниже.

Нахождение координат точки пересечения двух прямых на плоскости

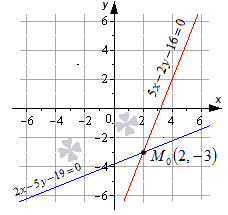
Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что

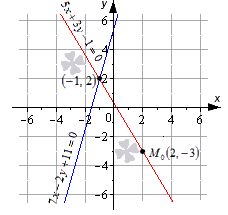
Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.

Получившиеся числа являются координатами, которые необходимо было найти.

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

Отсюда имеем, что координаты – это точка пересечения

Применим метод Крамера для нахождения координат:

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Следует собрать уравнения в систему для последующего решения:

Ответ: заданные уравнения определяют одну и ту же прямую.

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

Ответ: точек пересечения нет, прямые параллельны.

Для решения составляем систему уравнений. Получаем

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0

Рассмотрим подобные задания на примерах.

Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

Источник

Точка и прямая

Точка и прямая являются основными геометрическими фигурами на плоскости.

Определение точки и прямой в геометрии не вводят, эти понятия рассматриваются на интуитивно-понятийном уровне.

Точки обозначают прописными (заглавными, большими) латинскими буквами: A, B, C, D, …

Прямые обозначают одной строчной (маленькой) латинской буквой, например,

Прямая состоит из бесконечного множества точек и не имеет ни начала, ни конца. На рисунке изображают только часть прямой, но понимают, что она простирается в пространстве бесконечно далеко, неограниченно продолжаясь в обе стороны.

О точках, которые лежат на прямой, говорят, что они принадлежат этой прямой. Принадлежность отмечают знаком ∈. О точках вне прямой говорят, что они не принадлежат этой прямой. Знак «не принадлежит» — ∉.

Например, точка B принадлежит прямой a (пишут: B∈a),

точка F не принадлежит прямой a, (пишут: F∉a).

Основные свойства принадлежности точек и прямых на плоскости:

Каковы бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и притом только одну.

Прямые также обозначают двумя большими латинскими буквами, по названию точек, которые лежат на прямой.

— эту прямую можно назвать MK или MN или NK.

Две прямые могут пересекаться и не пересекаться. Если прямые не пересекаются, они не имеют общих точек. Если прямые пересекаются, они имеют одну общую точку. Знак пересечения — ∩.

Например, прямые a и b пересекаются в точке O

(пишут: a ∩ b=O).

Прямые c и d также пересекающиеся, хотя на рисунке нет их точки пересечения.

Прямые m и n не имеют общих точек.

Источник

Пересекающиеся прямые

Если две прямые имеют общую точку, то говорят, что эти прямые пересекаются. Такие прямые называют пересекающимися прямыми:

Точка пересечения — это точка, общая для двух или более геометрических фигур.

Перпендикуляр и наклонная

При пересечении вертикальной и горизонтальной прямой линии образуется четыре прямых угла. Такие линии, относительно друг к другу, называются перпендикулярными линиями или просто перпендикулярами:

Даже если прямые не являются вертикальной и горизонтальной линиями, но при пересечении образуют четыре прямых угла, то они всё равно являются перпендикулярными:

Если прямая линия пересекает другую не под прямым углом, то такая линия называется наклонной к прямой, которую она пересекает. При этом образуется четыре угла: два из них будут острыми и два тупыми:

Образованные острые углы равны и относительно друг друга будут называться вертикальными углами. То же самое можно сказать и об образованных тупых углах — они равные и вертикальные.

Источник