Как определить что перед тобой данные случайные погрешности
Определение случайной погрешности
Случайные погрешности приводят к тому, что наблюдаемые значения измеряемой величины при многократных измерениях случайным образом рассеяны относительно ее истинного значения. Тогда действительное значение находится как наиболее вероятное из серии опытов, а погрешность характеризуют шириной интервала, который с заданной вероятностью включает истинное значение. Математическое обоснование этих положений дается в теории вероятностей, применение которой для обработки результатов измерений приведено в литературе 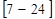
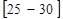
Очень часто студенты и школьники находят погрешность измерения по формуле
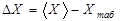
где 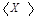
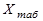
Кроме того, часто погрешность вычисляется как среднее значение отклонений отдельных результатов измерений от среднего значения по формуле
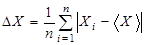
Согласно такому подходу, любое значение погрешности появляется одинаково часто, т.е. разные по величине погрешности считаются равновероятными. Этот метод можно использовать в лабораторных работах при малом числе измерений.
Однако случайные погрешности не являются равновероятными. Они требуют для своего определения статистической обработки результатов измерения. Поэтому представляется необходимым рассмотреть содержание статистической обработки результатов измерений. В основе статистической теории погрешностей лежат следующие положения:
1) при большом числе измерений наблюдаются случайные погрешности одинаковой величины, но разного знака, т. е. погрешности, как в сторону уменьшения, так и в сторону увеличения, встречаются одинаково часто;
2) большие (по абсолютной величине) погрешности встречаются реже, чем малые, т.е. вероятность появления погрешности уменьшается с ростом величины погрешности;
3) погрешности измерений могут принимать непрерывный ряд значений.
Распределение случайной величины, которое подчиняется перечисленным свойствам, называется нормальным распределением. Для оценки разбросов отдельных значений случайной величины с нормальным распределением или отдельных отсчетов в теории нормального распределения выбирается выборочное среднее квадратичное отклонение отсчетов,которое вычисляется по формуле:
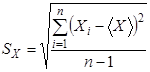
Оценка величины погрешности одного измерения, определяемая формулой (6.4) очень важна. Однако для измерения важной задачей является определение, с какой точностью среднее значение измеряемой величины соответствует искомой величине. Эта задача возникает в связи с тем, что среднее значение может быть получено из разных измерений. Например, среднее значение может быть получено при различном числе измерений. Поэтому эмпирическое среднее значение также является случайной величиной, которая также может описываться функцией распределения. Соответствующая этой функции величина среднего квадратичного отклонения 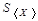
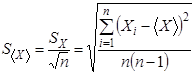
Эта величина называется выборочным средним квадратичным отклонением среднего значенияилистандартной ошибкой.
Как видно из формулы стандартной ошибки (6.5), она уменьшается с ростом числа измерений и точность результата возрастает, что и соответствует предыдущим рассуждениям.
Рассмотренные выше формулы для определения ошибки измерения используют характеристики нормального распределения случайной величины. Однако неизвестно, по какому закону распределены результаты измерений. Поэтому эти оценки являются приближенными. В связи с этим возникает необходимость анализа этого подхода к определению погрешности измерения. Для такого анализа можно использовать известное в теории вероятностей 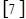
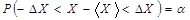
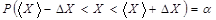
Величина 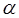
Доверительным интервалом называется интервал значений 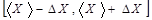
Таким образом, для определения случайной погрешности необходимо найти или задать два числа: а именно величину самой случайной погрешности или доверительного интервала и величину доверительной вероятности.
Для любой величины доверительного интервала можно рассчитать доверительную вероятность. Для этого используется функция Лапласа, которая также называется интегралом вероятностей. Функция Лапласа имеет вид:
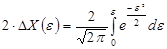
где 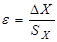
Результаты этой таблицы показывают, что средней квадратичной ошибке 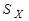
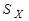
Доверительные вероятности 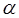
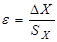
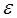 | 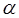 | 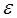 | 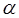 | 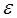 | 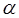 |
| 1,2 | 0,77 | 2,6 | 0,990 | ||
| 0,05 | 0,04 | 1,3 | 0,80 | 2,7 | 0,993 |
| 0,1 | 0,08 | 1,4 | 0,84 | 2,8 | 0,995 |
| 0.15 | 0,12 | 1,5 | 0,87 | 2,9 | 0,996 |
| 0,2 | 0,16 | 1,6 | 0,89 | 3,0 | 0,997 |
| 0,3 | 0,24 | 1,7 | 0,91 | 3,1 | 0,9981 |
| 0,4 | 0,31 | 1,8 | 0,93 | 3,2 | 0,9986 |
| 0,5 | 0,38 | 1,9 | 0,94 | 3,3 | 0,9990 |
| 0,6 | 0,45 | 2,0 | 0,95 | 3,4 | 0,9993 |
| 0,7 | 0,51 | 2,1 | 0,964 | 3,5 | 0,9995 |
| 0,8 | 0,57 | 2,2 | 0,972 | 3,6 | 0,9997 |
| 0,9 | 0,63 | 2,3 | 0,978 | 3,7 | 0,9998 |
| 1,0 | 0,68 | 2,4 | 0,984 | 3,8 | 0,99986 |
| 1.1 | 0,73 | 2,5 | 0,988 | 3,9 | 0,99990 |
| 4,0 | 0,99993 |
Случайную погрешность принято определять как полуширину доверительного интервала. Размер доверительного интервала задается в виде значения кратного выборочному среднему квадратичному отклонению среднего значения 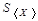
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В чем главное различие между случайными и систематическими погрешностями измерений?
Систематические погрешности входят в каждый результат измерений по строго определённому закону; их делят на постоянные, то есть неизменные по знаку и величине, и переменные – изменяющие свою величину от одного измерения к другому по определённому закону. Источником систематических погрешностей могут быть, например, неправильная длина мерного прибора, личная погрешность наблюдателя и так далее. Такие погрешности должны быть обнаружены, изучены и исключены из результатов наблюдений путём введения соответствующих поправок.
Случайные погрешности носят случайный характер, их возникновение не подчиняется определённым математическим законам, они связаны между собой статистической закономерностью, то есть проявляются в массовых явлениях.
41. Какими свойствами обладают случайные погрешности?
Свойства случайных погрешностей. Случайные погрешности можно определить как разность между измеренными и истинными значениями одной и той же величины. На основании теоретического и практического изучения многих рядов случайных погрешностей выведены их общие свойства:
1 При данных условиях случайные погрешности не могут превышать определенного предела.
2 Одинаковые по абсолютной величине положительные и отрицательные погрешности равновозможны.
3 Меньшие по абсолютной величине погрешности встречаются чаще, чем большие.
4 Среднее арифметическое из случайных погрешностей равноточных измерений одной и той же величины имеет тенденцию стремится к нулю при неограниченном увеличении числа измерений.
42. Почему среднее арифметическое из результатов равноточных измерений является вероятнейшим значением измеряемой величины?
Складывая левые и правые части этих равенств, получим
В теории погрешности принято обозначать сумму величин через квадратные скобки, например:Δ1 + Δ2 + … + Δn = [Δ]; l1 + l2 + … + ln = [l] и т. д.
При этих обозначениях равенство примет вид
Согласно четвертому свойству случайных погрешностей величина [Δ] / n в равенстве при неограниченном возрастании числа измерений стремится к нулю. Следовательно, величина [l] / n при этих условиях будет приближаться к истинному значению Х. На основании этого арифметическую середину (среднее арифметическое из результатов измерений) принято считать наиболее надежным или вероятнейшим результатом из равноточных измерений одной и той же величины при любом числе измерений.
43. Как вычисляют истинные и вероятнейшие погрешности?
Рассмотрим одно из важнейших свойств вероятнейших погрешностей. Для этого напишем и просуммируем почленно уравнения, по которым вычисляют каждую из погрешностей ряда
Согласно ( nL =∑ l Следовательно, ∑ v = О. Это свойство используют для контроля правильности вычисления арифметического среднего. Если сумма вероятнейших погрешностей равна нулю, вероятнейшее значение измеренной величины вычислено верно.
44. Точность измерения каких величин оценивают абсолютной и относительной погрешностью? Как представляют относительную погрешность в геодезии?
Разность между результатом измерения некоторой величины (l) и ее истинным значением (X) называют абсолютной (истинной) погрешностью.
Истинное (абсолютно точное) значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершенную методику измерений. Лишь в отдельных случаях может быть известно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.
Разность суммы практически измеренных (или вычисленных) величин и теоретического ее значения называется невязкой. Например, теоретическая сумма углов в плоском треугольнике равна 180º, а сумма измеренных углов оказалась равной 180º02′; тогда погрешность суммы измеренных углов составит +0º02′. Эта погрешность будет угловой невязкой треугольника.
Абсолютная погрешность не является, полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,5 м, а отрезок длиною 200 м – с ошибкой 0,2 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому вводят понятие относительной погрешности:
Отношение абсолютной погрешности измеряемой величины Δ к измеренной величине l называют относительной погрешностью.
Относительные погрешности всегда выражаются дробью с числителем, равным единице (аликвотная дробь). Так, в приведенном выше примере относительная погрешность первого измерения составляет 
а второго 
Относительную погрешность вводят в основном для оценки точности измененных линейных величин, длин линий в полигонометрическом ходе, например, точнее линейной невязки.
45. Вычислить объем грунта, необходимого для подсыпки высотой 1.05 м. если площадка имеет форму прямоугольника с размерами 100.45 и 151.55 м. учитывая, что приведенные цифры приближенные
V = a * b * c=100,45*151,55*1,05=15984.4 м 3
46. Объяснить сущность понятий «горизонталь», «высота сечения рельефа», «заложение», «мера крутизны скатов».
Горизонталь— линия на карте, соединяющая точки рельефа с одинаковой высотой над уровнем моря.
Высота сечения рельефа— расстояние между двумя смежными основными горизонталями по высоте. Высоту сечения рельефа подписывают на каждом листе карты под ее масштабом.
заложения горизонталей, т. е. расстояния в плане между смежными горизонталями, зависят от крутизны ската: чем скат круче, тем меньше заложение. Следовательно, по величине заложения можно судить о крутизне ската.
Мерою крутизны склона служит уклон, или тангенс угла наклона линии местности к плоскости горизонта.
Случайные и систематические погрешности
Говоря о погрешностях измерений, следует, прежде всего, упомянуть о грубых погрешностях (промахах), возникающих вследствие недосмотра экспериментатора или неисправности аппаратуры. Такие ошибки происходят, если, например, экспериментатор неправильно прочтет номер деления на шкале, если в электрической цепи произойдет замыкание и вследствие других подобных причин. Грубых ошибок следует избегать. Если установлено, что они произошли, соответствующие измерения нужно отбрасывать.
Не связанные с грубыми ошибками погрешности опыта делятся на случайные и систематические. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего. Погрешности, меняющие величину и знак от опыта к опыту, называют случайными.
Случайные погрешности могут быть связаны с сухим трением (из-за которого стрелка прибора вместо того, чтобы останавливаться в правильном положении, «застревает» вблизи него), с люфтами в механических приспособлениях, с тряской, которую в городских условиях трудно исключить, с несовершенством объекта измерений (например, при измерении диаметра проволоки, которая из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение) или с особенностями самой измеряемой величины. Рассмотрим последний случай.
Пусть мы измеряем число космических частиц, проходящих в минуту через счетчик. При достаточно больших размерах счетчика это число может составлять несколько сот или даже тысяч. Пусть в первую минуту через счетчик прошло 345 частиц. Повторяя измерение, найдем, что в разных опытах получаются разные числа (вообще говоря, не слишком отличающиеся от 345). Это происходит потому, что в нашем случае число частиц, проходящих в минуту через счетчик, является случайной величиной. Космическое излучение правильно характеризовать не числом частиц, которые прошли через счетчик за выбранную минуту, а средним числом частиц, проходящих в минуту через счетчик, и средним отклонением чисел в различных опытах.
Не следует думать, что, говоря о прохождении космических частиц через счетчик, мы выбрали исключительное явление. Подобный разброс результатов измерения наблюдается при изучении (с помощью счетчиков) числа распадов в радиоактивных источниках, при изучении очень слабых токов, когда через измерительный прибор за время измерения проходит не очень большое число электронов или ионов (например, в чувствительных масс-спектрометрах), и во многих других случаях.
Случайные погрешности эксперимента исследуются путем сравнения результатов, полученных при нескольких опытах, поставленных в одинаковых условиях. Два-три измерения следует производить всегда. Если результаты совпали, то на этом следует остановиться. Если же они расходятся, нужно попытаться понять причину расхождения. Часто она связана с тем, что прибор неисправен, ненадежно закреплен или плохо смазан, что электрические контакты не пропаяны или недостаточно зажаты. В этом случае, прежде всего, нужно попытаться исправить аппаратуру. Если устранить причину не удается, нужно произвести несколько измерений и записать все полученные результаты. Ниже мы расскажем о том, как следует поступать с полученными числами.
Систематические погрешности сохраняют свою величину. (и знак!) во время эксперимента. Они могут быть связаны с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического, винта, не равные плечи весов) и с самой постановкой опыта (определение скорости поезда по проходимому им расстоянию на участке, где движение происходит с небольшим ускорением, которое ускользнуло от внимания экспериментатора, влияние трения и т. д.). В результате систематических погрешностей разбросанные из-за случайных ошибок результаты опыта колеблются не вокруг истинного, а вокруг некоторого смещенного значения.

пренебрежимо мала. Измеренные значения отличаются от истинного вследствие случайных ошибок: опыта. На рис. 1, б изображены результаты опыта при наличии как случайных, так и систематических погрешностей.
При желании систематические погрешности опыта могут быть изучены и скомпенсированы путем внесения поправок в результаты измерений. Неравноплечность весов можно исследовать, меняя местами грузы на чашках весов. Неточность шкал электроизмерительных приборов можно установить, сравнивая их показания с показаниями более точных приборов, и т. д. Как правило, этого не делают. Если систематическая погрешность опыта для выбранной цели слишком велика, то обычно оказывается проще поставить новые, более точные приборы, чем исследовать погрешности старых.
Не следует думать, что различие между случайными и систематическими погрешностями является абсолютным. Оно связано с постановкой опыта. Производя измерения тока не одним, а несколькими разными амперметрами, мы превращаем систематическую ошибку, связанную с неточностью шкалы, в случайную ошибку, величина (и знак!) которой зависит от того, какой поставлен амперметр в данном опыте и т. д. Однако во всяком данном опыте – при заданной его постановке – различие между систематическими и случайными погрешностями всегда можно и нужно устанавливать с полной определенностью.
Случайные погрешности
Случайные величины, к которым относятся случайные погрешности, изучаются в теории вероятностей и в математической статистике. Мы здесь опишем – с пояснениями, но без доказательств – основные свойства и основные правила обращения с такими величинами в том объеме, который необходим для обработки результатов измерений, полученных в лаборатории. В этом параграфе мы будем предполагать, что систематические погрешности пренебрежимо малы и все ошибки сводятся к случайным. Позднее, в § 5, мы обсудим, как следует поступать в тех случаях, когда нужно принимать во внимание как случайные, так и систематические погрешности опыта.
Рассмотрим для примера данные, полученные при измерении массы тела на весах, у которых имеется область застоя из-за трения призмы на подушке (разброс результатов для наглядности преувеличен). Пусть масса тела близка к 48 мг, результат измерений удается отсчитать по шкале с точностью до 0,1 мг. Имеем:
| № опыта | |||||||||||
| Масса, мг | 48,0 | 47,9 | 47,5 | 48,2 | 48,4 | 47,8 | 48,6 | 48,3 | 47,8 | 48,1 | 48,2 |
Вместо одного нужного нам результата мы получили одиннадцать. Что делать с полученными цифрами? Как найти из них достаточно близкое к истинному значение массы тела и как оценить погрешность полученного результата? Этот вопрос подробно изучается в математической статистике. Мы здесь изложим соответствующие правила без вывода.
В качестве наилучшего значения для измеренной величины обычно принимают среднее арифметическое из всех полученных результатов:

В нашем случае получим
Этому результату следует приписать погрешность, определяемую формулой

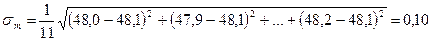
Результат опыта записывается в виде
В нашем случае m = (48,10± 0,10)мг.
Рассмотрим формулы (3) и (4). Прежде всего, попытаемся понять, как зависит результат расчета от числа измерений. Формула (3) показывает, что xср от числа измерений зависит слабо. Все слагаемые, входящие в числитель, приблизительно равны друг другу. Их сумма пропорциональна числу слагаемых. После деления на знаменатель получается величина, мало зависящая от числа измерений. Так, конечно, и должно быть. Среднее измеренное значение – при правильной методике опыта – всегда лежит вблизи истинного значения и в разных независимых сериях измерений испытывает вокруг него небольшие случайные колебания.
Погрешность опыта, определяемая формулой (4), с увеличением числа измерений п уменьшается как 

(Число членов суммы в (4) растет как п, числитель (4) поэтому увеличивается как 

Формула (4) может быть записана в несколько ином виде

При такой записи множитель 1/ 

При обсуждении смысла величины σ следует помнить, что истинную величину погрешности невозможно узнать до тех пор, пока из каких-либо других опытов (или соображений) не удастся определить искомую величину с существенно лучшей точностью. Но тогда рассматриваемые опыты потеряют значение, и их погрешность никого не будет интересовать. Как уже отмечалось, погрешность результата не столько определяют, сколько оценивают. Оценка (4) подобрана так, что при проведении многочисленных серий измерений погрешность в 2/3 случаев оказывается меньше σx, а в 1/3 случаев больше, чем σx.
Иначе говоря, если бы мы – в нашем случае – провели не одну серию из 11 взвешиваний, а десять таких серий, то мы могли бы ожидать, что в шести или семи из них усредненный результат будет отличаться от истинной массы тела меньше чем. на 0,1 мг. а в остальных случаях больше, чем, на 0,1 мг.
Погрешность, определенную с достоверностью 2/3, обычно называют стандартной (или среднеквадратичной) погрешностью опытов, а ее квадрат – дисперсией. Можно показать, что, как правило, погрешность опыта только в 5% случаев превосходит ±2σ и почти всегда оказывается меньше ±3σ.
На первый взгляд из сказанного можно сделать вывод, что, беспредельно увеличивая число измерений, можно даже с самой примитивной аппаратурой получить очень хорошие результаты. Это, конечно, не так. С увеличением числа измерений уменьшается только случайная погрешность опытов. Методические погрешности и погрешности, связанные с несовершенством приборов (например, с неправильностью их шкалы), при увеличении числа опытов не меняются. В приведенном выше примере результат взвешивания округлялся до десятых долей миллиграмма. Это-делалось потому, что сотых долей отсчитать было нельзя. Одна только ошибка отсчета составляет при этом около 0,1 мг. Поэтому погрешность результата ни при каком числе опытов не может быть сделана меньше. Число опытов в нашем случае было-выбрано разумно. Из приведенных в таблице цифр ясно, что при однократном измерении мы могли ошибиться на несколько десятых. Среди цифр встречаются результаты, отличающиеся на 0,3 и даже на 0,5 от среднего. После усреднения по 11 измерениям погрешность существенно уменьшилась. Но если окажется нужным узнать массу тела с лучшей, чем это мы сделали, точностью, то недостаточно просто увеличить число измерений. Придется взять более точные весы, позволяющие производить измерения не до десятых, а, скажем, до сотых долей миллиграмма.
Скажем несколько слов о формуле (4). Эта формула позволяет хорошо оценивать величину стандартной погрешности в тех случаях, когда число опытов оказывается не меньше 4–5. При меньшем числе опытов лучше применять другие, более сложные оценки. Их мы, однако, рассматривать не будем, во-первых, чтобы не удлинять и не усложнять текста, а, во-вторых, по той причине, что надежность всех этих оценок при малом числе измерений оказывается невысокой.
Систематические погрешности
Оценку систематических погрешностей экспериментатор производит, анализируя особенности методики, паспортную точность приборов и производя контрольные опыты.
Систематические погрешности электроизмерительных приборов, выпускаемых промышленностью (амперметров, вольтметров, мостов, потенциометров и т. д.), определяются их классом точности, который обычно выражают в процентах. Амперметр класса 0,2 (если он, конечно, исправен и проходит систематическую проверку) позволяет производить измерения с абсолютной погрешностью, не превосходящей 0,2% от тока, соответствующего полной шкале прибора. На всех участках шкалы – в ее начале, середине и конце – эта погрешность одна и та же.
Как уже отмечалось, класс электроизмерительных приборов определяет максимальную погрешность, величина которой не меняется при переходе от начала к концу шкалы. Относительная ошибка при этом резко меняется, поэтому приборы обеспечивают хорошую точность при отклонении стрелки почти на всю шкалу и не дают ее при измерениях в начале шкалы. Отсюда следует рекомендация: выбирать прибор (или шкалу многошкального прибора) так, чтобы стрелка прибора при измерениях заходила за середину шкалы.
Говоря о систематических погрешностях опыта, следует сказать несколько слов об ошибке отсчета «на глаз». Большинство приборов не имеет нониуспых шкал. При этом доли деления отсчитываются на глаз. Эта ошибка составляет 1–2 десятых доли деления. При отсчетах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для облегчения установки глаза на многих приборах устанавливается зеркало («зеркальные приборы»). Глаз экспериментатора установлен правильно, если стрелка прибора закрывает свое изображение в зеркале. При работе с электроизмерительными приборами отсчет должен включать число целых делений и число десятых долей деления, если отсчет может быть произведен с этой точностью (если стрелка или зайчик не ходят и не дрожат, что может сделать аккуратный отсчет невозможным).
Поясним указанное правило. Шкалы электроизмерительных приборов обычно изготовляют так, что одно деление шкалы приблизительно равно максимальной погрешности прибора. Зачем же в этом случае отсчитывать десятые доли деления? Ответ на этот вопрос читатель найдет в § 7. Забегая вперед, отметим, что при измерениях, при расчетах и при записи результатов, кроме надежно известных значащих цифр, всегда указывается одна, лишняя. Такая процедура, среди прочих, имеет и то преимущество, что позволяет вовремя замечать мелкие нерегулярности исследуемых зависимостей. Если, например, стрелка прибора при измерениях отклонилась на полделения назад, этот результат является надежным и в том случае, когда погрешность прибора равна целому делению.
Несколько слов о точности линеек. Металлические линейки очень точны: миллиметровые деления наносятся с погрешностью не более ±0,05 мм, а сантиметровые – не хуже, чем с точностью 0,1 мм. Погрешность измерений, производимых с помощью таких линеек, практически равна погрешности отсчета на глаз. Деревянными или пластиковыми линейками лучше не пользоваться: их погрешности неизвестны и могут оказаться неожиданно большими. Исправный микрометр обеспечивает точность 0,01 мм, а погрешность измерений штангенциркулем определяется точностью, с которой может быть сделан отсчет, т. е. точностью нониуса (у штангенциркулей цена делений нониуса составляет обычно 0,1 или 0,05 мм).

