Как определить что угол прямой 3 класс
Что такое угол? Виды углов
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
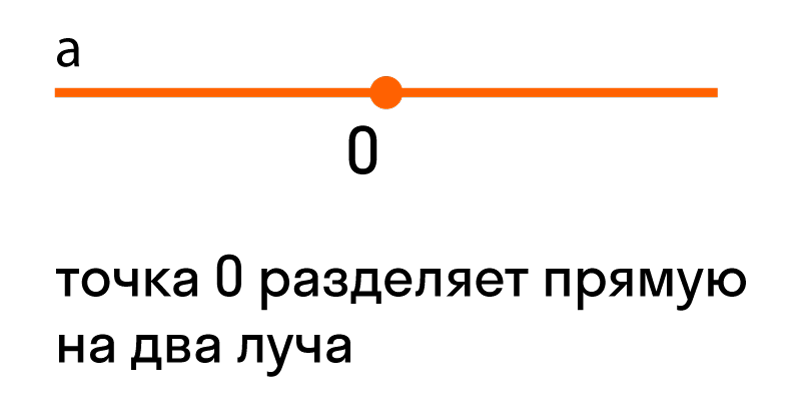
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
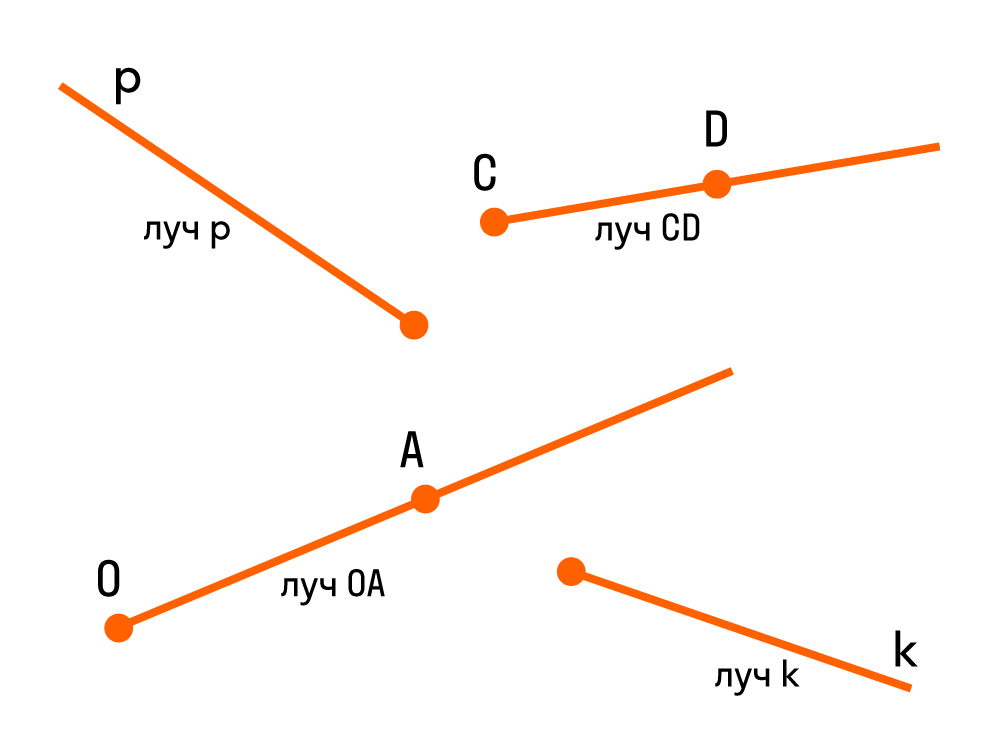
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
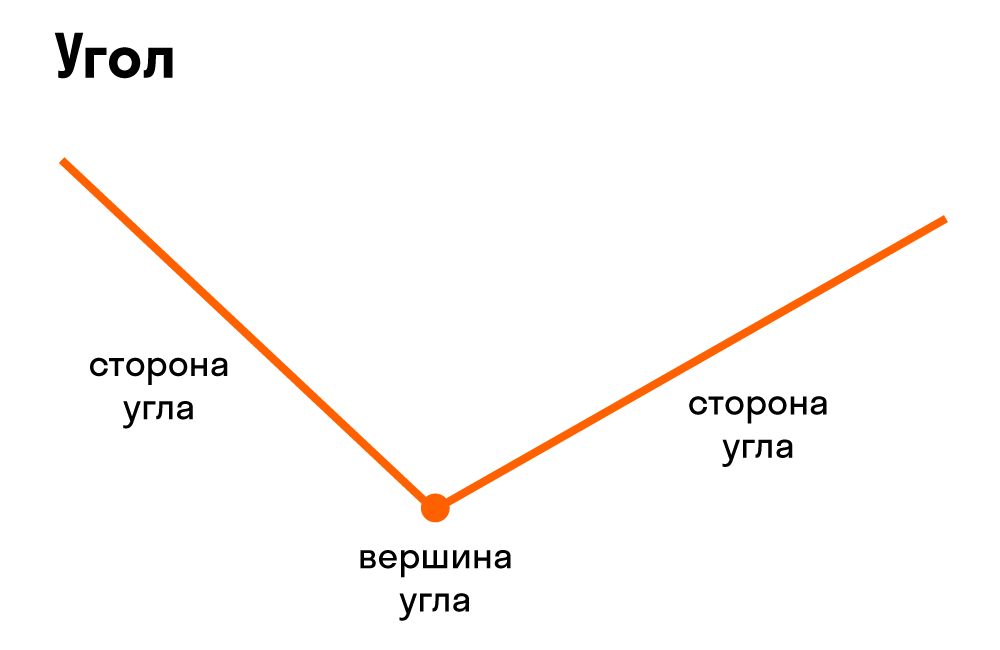
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
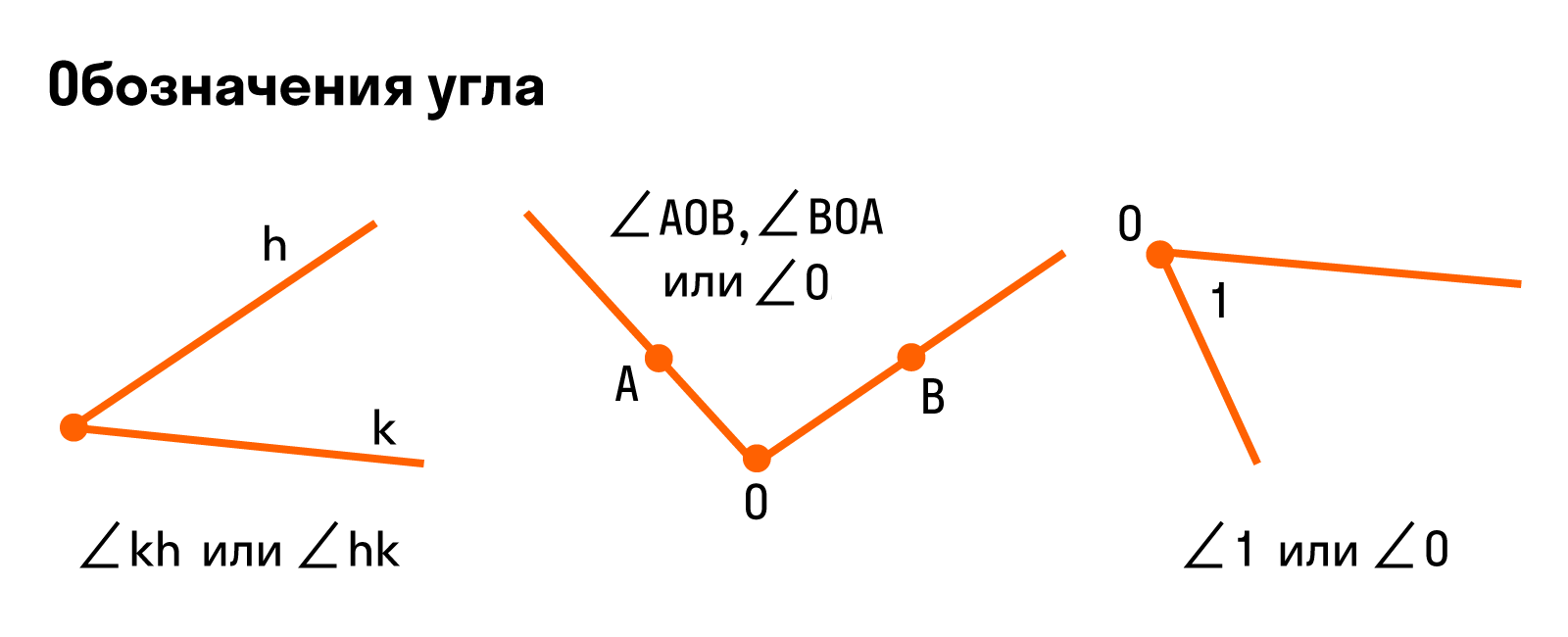
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
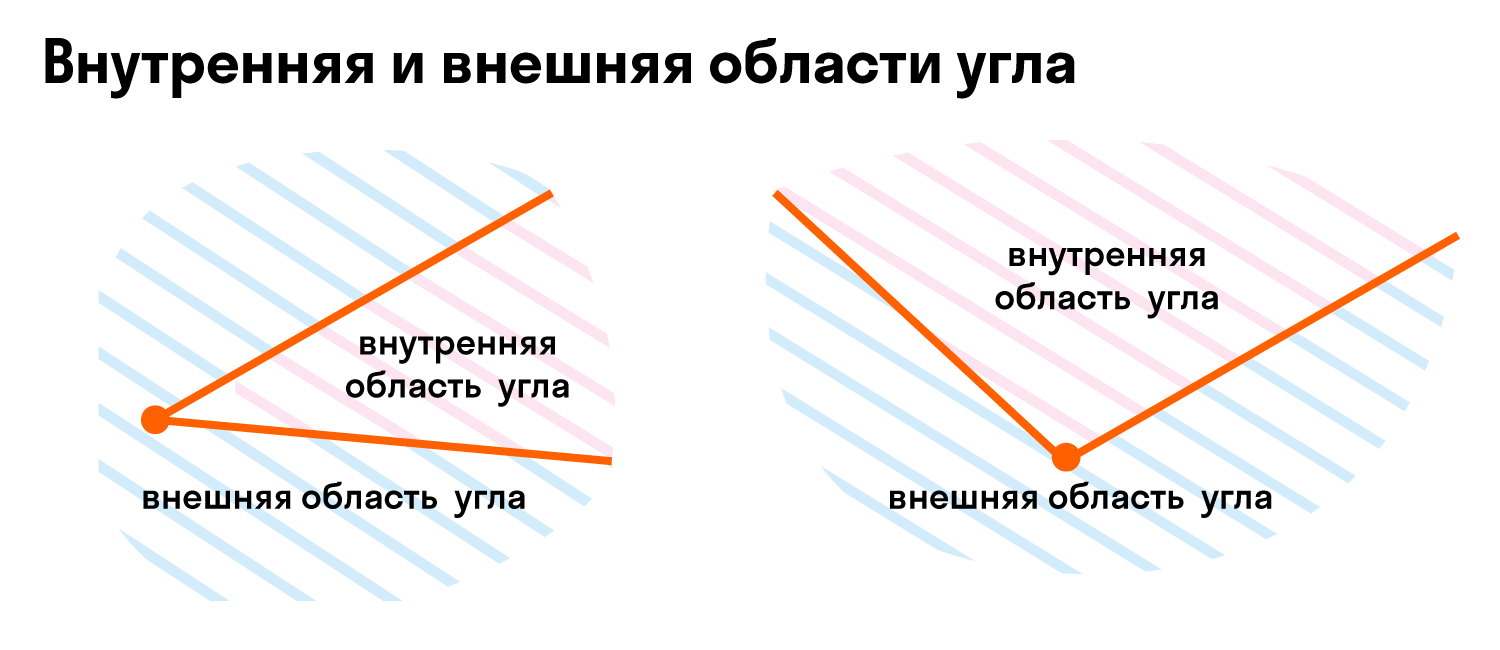
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
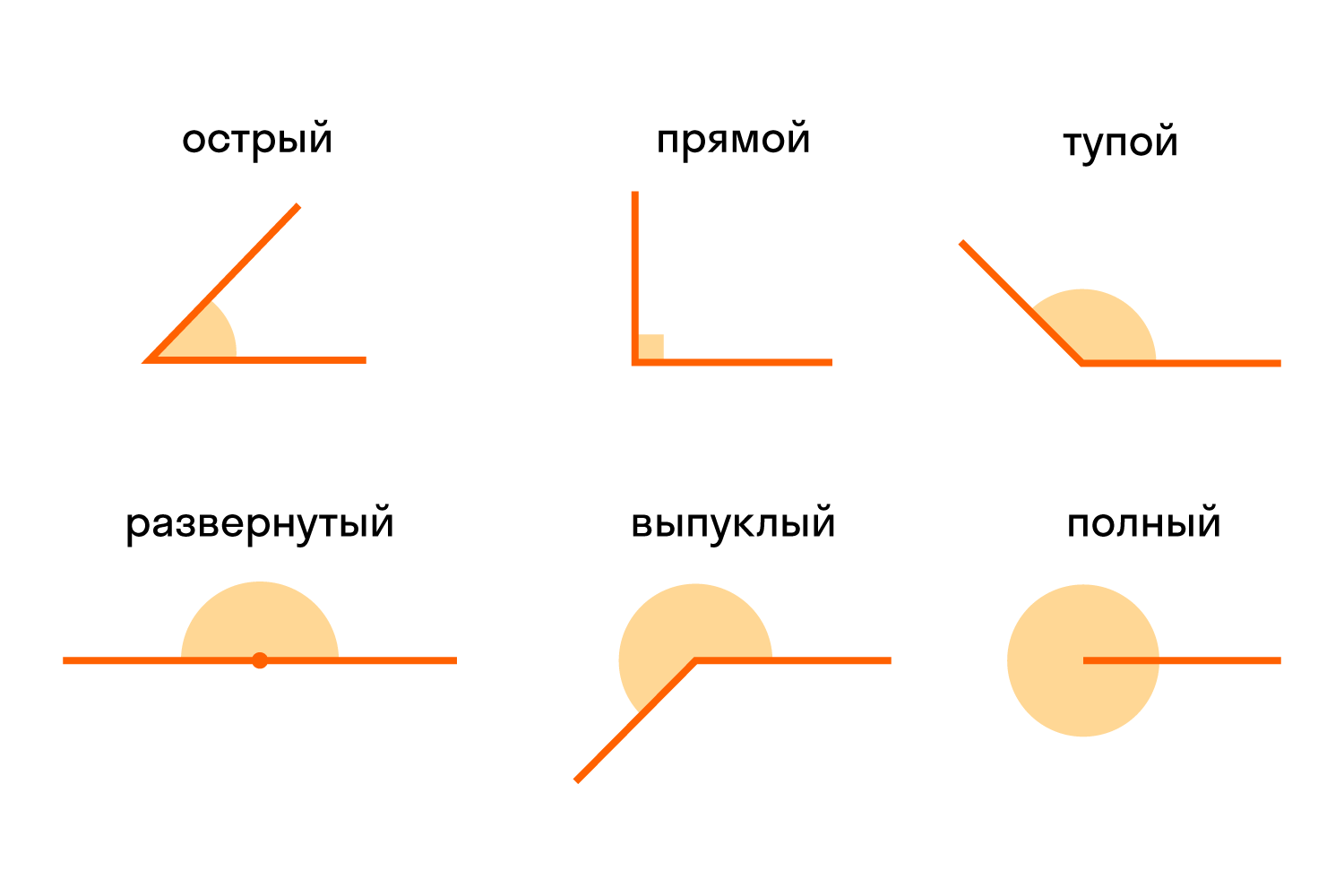
Виды углов
Есть разные типы углов и у каждого своё название:
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.
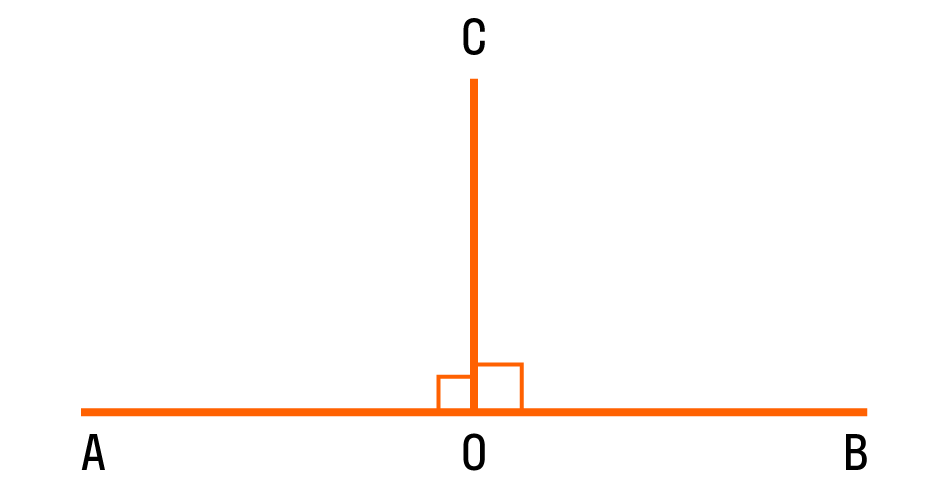
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
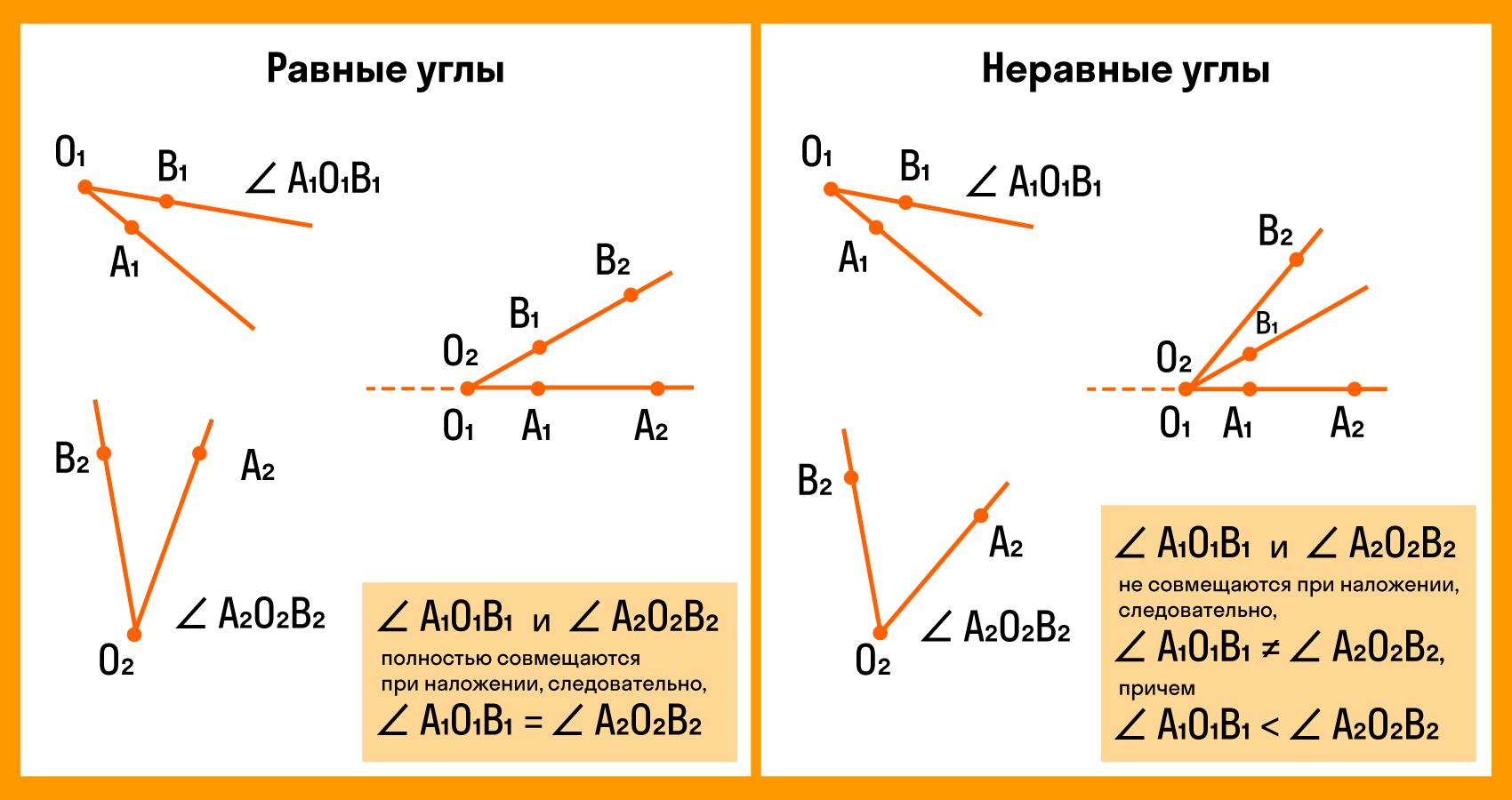
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
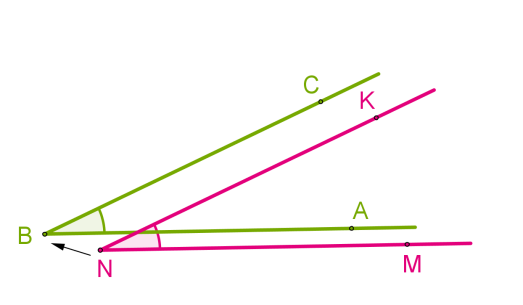
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
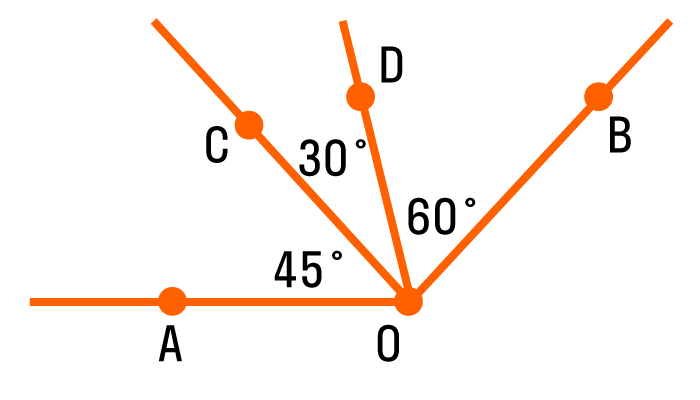
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.
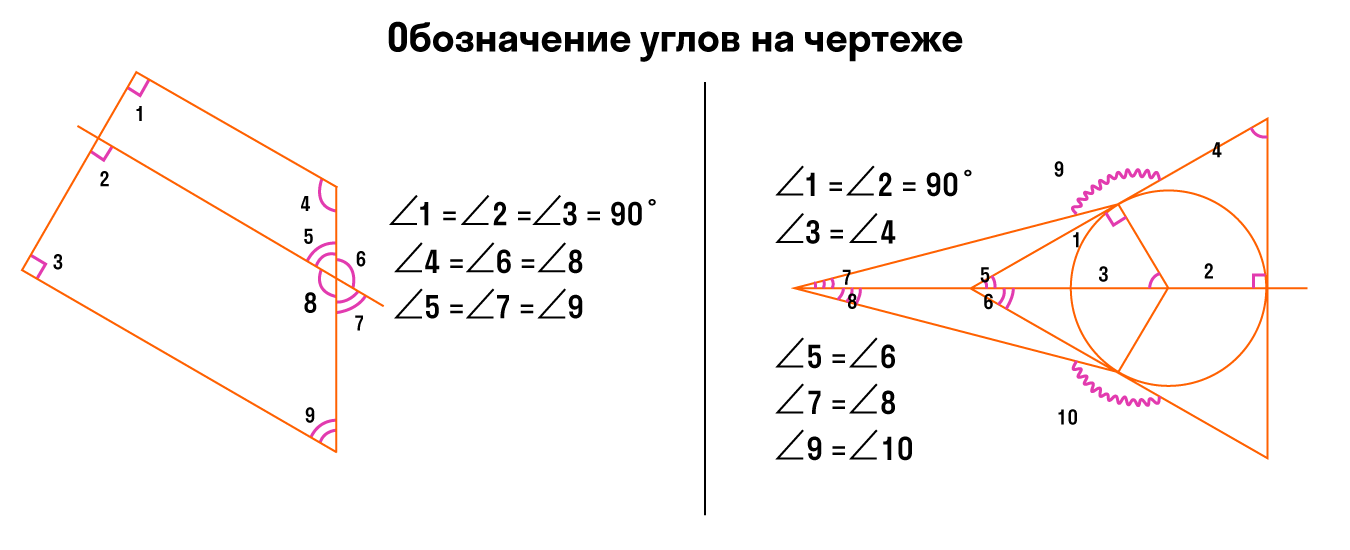
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
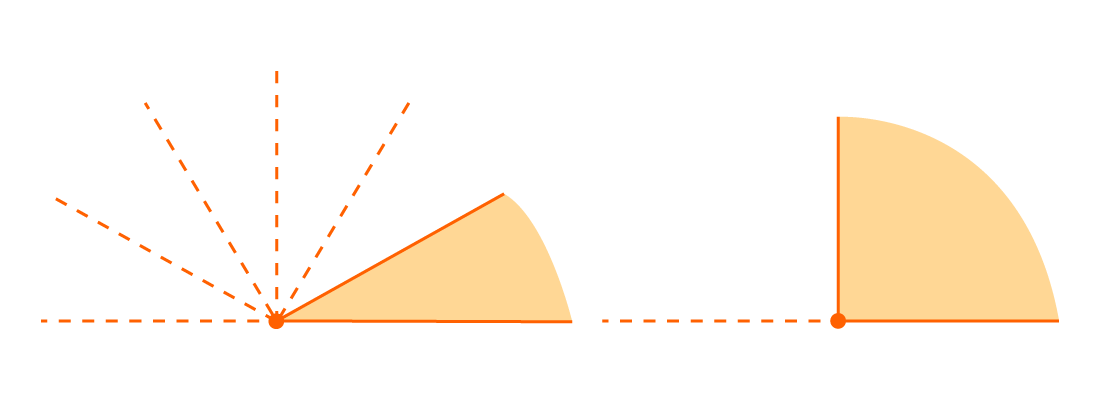
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Конспект урока по математике «Прямой угол» (3 класс) УМК «Школа России»
Учитель: войтенко Юлия николаевна
тип: урок изучения нового и первичного закрепления .
Цели: дать учащимся представление о прямом угле;
учить отличать прямой угол от острого и тупого углов при помощи модели прямого угла;
развивать вычислительные навыки, умение складывать и вычитать двузначные числа в столбик (без перехода через десяток).
— обучающие: ознакомление учащихся с понятием «прямой угол»;
формирование практических навыков определения прямого угла при помощи модели и без нее;
продолжение работы по совершенствованию навыка устного счёта в пределах 100;
—развивающие: развитие логического мышления, внимания, памяти, пространственного воображения;
развитие культуры речи и эмоций учащихся;
—воспитательные: развитие познавательной активности;
воспитание наблюдательности и любознательности;
воспитание взаимовыручки, стремления оказывать помощь в трудную минуту.
I. Организационный момент.
40…………(Дайте характеристику данных чисел)
2.Устный счет. «Какой пример лишний?»
(Лишними являются примеры 9 + 7, так как его значение равно шестнадцати, значения остальных выражений равны четырнадцати, и пример 10 + 4, так как во всех суммах складываются однозначные числа, а в этой сумме первым слагаемым является двузначное число.)
II. Постановка целей и задач урока.
– Какая из данных фигур «лишняя»? (Фигура 2.)
– Как называется эта фигура?
— Разделите фигуры на группы.
— По каким признакам можно разделить?
– Сегодня на уроке мы познакомимся с разными видами углов, их свойствами, научимся их обозначать буквами.
III. Первичное усвоение новых знаний.
На доске изображена фигура:
– Знаете ли вы, как называется эта фигура?
– Правильно, она называется углом.
Затем учитель изображает (или открывает ту часть доски, на которой изображён прямой угол).
Далее учащиеся рассматривают чертежи других углов, изображённых на доске.
– Все ли из этих углов прямые?
– Кроме прямых, бывают острые и тупые углы.
– Для того чтобы было легче определить, какой угол перед нами, сделаем модель прямого угла. Возьмите лист бумаги и перегните его 2 раза так, как показано на рис. 1 и 2 ваших учебников (с. 8, часть 2).
– Вы получили модель прямого угла.
– При помощи модели прямого угла определите в задании 1 (с. 8 учебника, часть 2), какие углы являются прямыми.
Все ребята повернулись,
Все ребята потянулись,
А потом они присели
И за парту тихо сели.
IV. Усвоение новых знаний.
– Начертите отрезок, длина которого равна 5 см.
– Ниже начертите отрезок на 2 см короче предыдущего.
– Используя данные отрезки, постройте ломаную линию.
– Какая фигура получилась?
— Какие углы в данной фигуре? Докажите свои высказывания.
– Найдите периметр полученного треугольника.
1. Сложение двузначных чисел в столбик.
Учащиеся выполняют задание 2 (с. 8 учебника, часть 2), в котором складывают и вычитают двузначные числа в столбик (без перехода через десяток) с последующей проверкой, также в столбик. Один ученик выполняет работу на доске.
2. Выполняется задание 3 (с. 8 учебника, часть 2).
Данное задание можно выполнить следующим образом: третий столбик устно (с объяснением), первый и второй столбики – с комментированием
VI. Домашнее задание. Инструктаж по его выполнению.
2. Начертить 2 фигуры, в которых были бы прямые углы.
VII. Рефлексия. Подведение итогов.
– Что нового узнали сегодня на уроке?
– Какие открытия сделали?
– Всё ли было понятно?
– Как вы сегодня работали?
– Чью бы работу вам хотелось отметить особенно?
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Краткое описание документа:
Конспект урока по ФГОС, УМК Школа России». Авторы учебника по математике 2 класс. Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Общая информация
Похожие материалы
«Почему вертолёт летает, если он не птица?»
Презентация районной учебно-исследовательской конференции «Юные исследователи»
Конспект по литературному чтению на тему «Обобщение по разделу «Зарубежная литература»» (3 класс)
Пример детского проекта «Наши друзья витамины»
Проектные задачи в начальной школе
Инженерная культура на уроках математики в начальной школе
Презентация к уроку русского языка на тему «Правописание частей слова.»
Урок математики в 1 классе «Перестановка слагаемых»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5400505 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Рособрнадзор объявил сроки и формат ЕГЭ
Время чтения: 1 минута
Дума приняла закон о бесплатном проживании одаренных детей в интернатах при вузах
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Что такое прямой угол
В данной публикации мы рассмотрим, что такое прямой угол, перечислим основные геометрические фигуры, в которых он встречается, а также разберем пример задачи по этой теме.
Определение прямого угла
Угол является прямым, если его градусная мера равняется 90 градусам.
На чертежах для обозначения такого угла используется не круглая дуга, а квадратная.
Фигуры с прямыми углами
1. Квадрат – ромб, все углы которого равны 90°.
2. Прямоугольник – параллелограмм, все углы которого, также, являются прямыми.
3. Прямоугольный треугольник – один из его углов прямой.
4. Прямоугольная трапеция – хотя бы один из углов равняется 90°.
Пример задачи
Известно, что в треугольнике один из углов является прямым, а два остальных равны между собой. Найдем неизвестные значения.
Решение
Как мы знаем из теоремы о сумме углов треугольника, она равняется 180°.
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 33. Угол. Виды углов: прямой, острый, тупой
Перечень вопросов, рассматриваемых в теме:
— Как распознавать углы?
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
Теоретический материал для самостоятельного изучения
Рассмотрите фигуры и выберите лишнюю.
Лишняя фигура под номером 2. Она образована незамкнутой линией.
Она называется угол.
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Посмотрите на рисунки: по-разному открытый веер, образует разные углы.
У каждого угла есть две стороны и вершина. Углы бывают прямые, острые и тупые. Углы определить можно помощью чертежного угольника.
Прямой угол определяем с помощью чертежного угольника.
Угол, который меньше прямого угла называется острым углом.
Угол, который больше прямого угла называется тупым углом.
Посмотрите, как из обычного листа бумаги можно сделать модель прямого угла. Моделью можно воспользоваться, если у вас нет чертежного угольника. Возьмите лист бумаги и перегните его 2 раза, как показано на рисунках 1 и 2. И получите модель прямого угла.
Разверните лист. Линии сгиба образовали 4 прямых угла.
Чтобы определить, какой угол начерчен, на него накладывают угольник или модель прямого угла.
Вывод: Углы могут быть прямыми и непрямыми. Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник. Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол – прямой. Не совпадут – непрямой. Непрямые углы делятся на: тупые и острые. Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.
1.Посмотрите на крыши домов и домиков. Какие углы ты видишь на рисунке? Соотнесите вид угла с изображением домика.
2. Выберите цифры, в записи которых присутствуют только прямые углы.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте, дорогие ребята!
Приглашаем вас в сказочную страну Геометрию.
Жил-был король Луч. Была у короля маленькая, смешная и забавная дочка Точка. Отец очень любил и баловал принцессу и никогда не наказывал: не ставил в угол за ее шалости.
Угол. Виды углов: прямой, тупой, острый
Ребята, а вы знаете, что такое угол? Какие бывают углы?
Давайте вместе начертим угол. Сначала поставим точку. Затем проведем из этой точки 2 луча. Например, так:
Лучи – это стороны угла. А точка, из которой мы проводили лучи – вершина угла.
Углы бывают прямые, острые и тупые. Острым углом назовем тот, который меньше прямого, а тупым углом – тот, который больше прямого угла.
Изготовим модель прямого угла из кусочка бумаги.
Можно в качестве модели прямого угла использовать угольник. У него обязательно есть один прямой угол.
Ребята, помогите принцессе Точке определить, какие углы являются прямыми, а какие тупыми и острыми! Сосчитайте, сколько на этом чертеже прямых, острых, тупых углов.
Прямых – 6 углов, острых – 4 угла, тупых – 2 угла.
Король Луч решил построить для принцессы Точки игровую площадку. Он долго размышлял, чертил на песке разные фигуры. Посмотрите, после дождя остались лишь очертания. Назовите одним словом, что это?
Верно, это углы. Запишите номера углов в 3 столбика: острые, тупые, прямые.
Прямоугольник. Свойства противоположных сторон прямоугольника
Ребята, посмотрите на дворец короля и принцессы. Из каких геометрических фигур он состоит?
Давайте сосчитаем все прямоугольники, квадраты, треугольники и круги.
Найдите среди этих фигур четырехугольники, у которых все углы прямые. Воспользуйтесь моделью прямого угла, которую мы с вами изготовили.
Ребята, у принцессы Точки есть для вас вопросы о прямоугольнике. Попробуйте на них ответить.
Вопрос 1. Равны ли у прямоугольника противоположные стороны (они лежат напротив друг друга)?
На чертеже противоположные стороны обозначены одинаковым цветом.
Подумайте! Возьмите любой прямоугольник, измерьте линейкой стороны фигуры, с помощью модели прямого угла или угольника проверьте углы.
Сравните свои выводы с правильными ответами.
Молодцы! Не огорчайтесь, если не все выводы совпали с правильными ответами. Давайте еще раз повторим о прямоугольнике все, что узнали.
Квадрат
Ребята, отвечая на вопрос принцессы Точки, мы сделали вывод о том, что у прямоугольника все стороны могут быть одинаковой длины. Такой прямоугольник будет называться квадратом.
Задача на смекалку от короля. Помогите принцессе Точке ее решить.
Начерти прямоугольник со сторонами 5 см и 4 см. Сделай из него квадрат! Подсказка: «Можно сделать двумя способами: добавить, убрать».
Принцесса отлично справилась с задачей. А теперь попробуйте вы самостоятельно выполнить следующее задание.
Найдите среди этих прямоугольников квадраты. Запишите их номера.
Поиграем вместе с принцессой Точкой. Она выложила из счетных палочек такую фигуру:
Сколько квадратов вы видите? Уберите одну палочку так, чтобы осталось два квадрата. Сделать это можно разными способами. Какие еще фигуры, кроме двух квадратов, у вас получились?
Кроме двух квадратов, на каждом рисунке есть прямоугольник.
Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге
Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.
Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.
Посмотрите, как получилось у принцессы. Сравните со своими чертежами.
Ставим точку. Откладываем два луча при помощи угольника или линейки.
Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.
А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.
Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.
Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол. Можно воспользоваться моделью прямого угла, которую мы изготовили.
Посмотрите, как это получилось у короля и Точки.
После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!
Сказка
Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:
У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.
Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».
Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:
Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.
Понравилась вам сказка? Давайте повторим о фигурах все, что узнали.
В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.
До скорой встречи в королевстве Геометрия! А сейчас проверьте свои знания. Принцесса Точка справилась с заданиями хорошо, допустила одну небольшую ошибку. Будьте внимательны, не спешите!