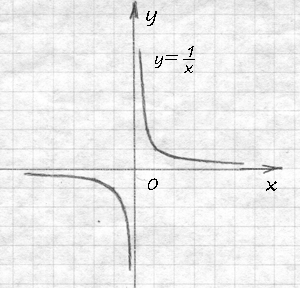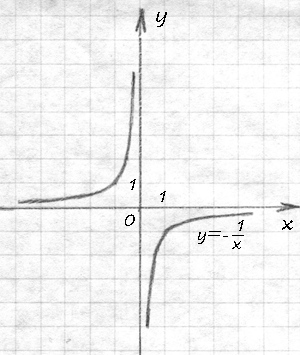Как понять что гипербола убывает
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Парабола
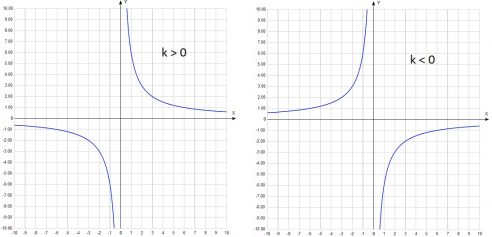
Гипербола
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>
Если k 0, ветви гиперболы проходят через II и IV четверти.
Квадратный корень
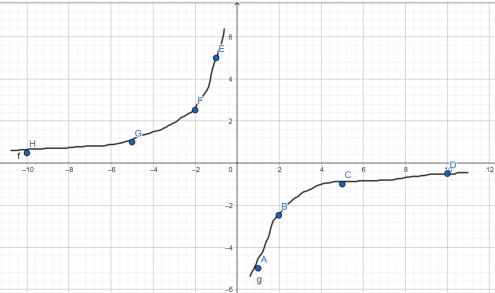
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Разбираемся с магией гиперболы
Здравствуйте, дорогие студенты вуза Аргемоны! Приветствую вас на очередной лекции по магии функций и интегралов.
Сегодня мы поговорим о гиперболе. Начнём от простого. Самый простой вид гиперболы:
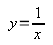
(1)
Эта функция, в отличии от прямой в её стандарных видах, имеет особенность. Как мы знаем, знаменатель дроби не может равняться нулю, потому что на ноль делить нельзя.
x ≠ 0
Отсюда делаем вывод, что областью определения является вся числовая прямая, кроме точки 0: (-∞; 0) ∪ (0; +∞).
Если х стремится к 0 справа (записывается вот так: х->0+), т.е. становится очень-очень маленьким, но при этом остаётся положительным, то у становится очень-очень большим положительным (y->+∞).
Если же х стремится к 0 слева (x->0-), т.е. становится по модулю тоже очень-очень маленьким, но остаётся при этом отрицательным, то у также будет отрицательным, но по модулю будет очень большим (y->-∞).
Если же х стремится в плюс бесконечность (x->+∞), т.е. становится очень большим положительным числом, то у будет становиться всё более и более меньшим положительным числом, т.е. будет стремиться к 0, оставаясь всё время положительным (y->0+).
Если же х стремится в минус бесконечность (x->-∞), т.е. становится большим по модулю, но отрицательным числом, то у будет тоже отрицательным всегда числом, но маленьким по модулю (y->0-).
у, как и х, не может принимать значения 0. Он только к нулю стремится. Поэтому множество значений такое же, как и область определения: (-∞; 0) ∪ (0; +∞).
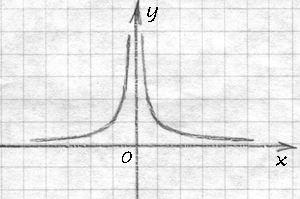
Исходя из этих рассуждений, можно схематически нарисовать график функции
Если совсем чуть-чуть изменить функцию: воспользоваться магией минуса,
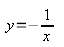
(1′)
то функция чудесным образом переместится из 1 и 3 координатных четвертей во 2-ю и 4-ю четверти и станет возрастающей.
Напомню, что функция является возрастающей, если для двух значений х1 и х2,таких, что х1 f(х2) для тех же значений х.
Ветви гиперболы приближаются к осям, но никогда их не пересекают. Такие линии, к которым приближается график функции, но никогда их не пересекает, называются ассимптотой данной функции.
Для нашей функции (1) ассимптотами являются прямые х=0 (ось OY, вертикальная ассимптота) и у=0 (ось OX, горизонтальная ассимптота).
А теперь давайте немного усложним простейшую гиперболу и посмотрим, что произойдёт с графиком функции.
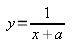
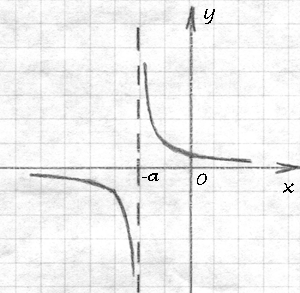
(2)
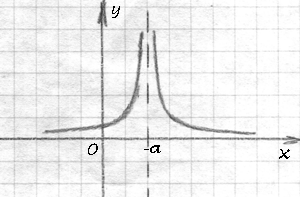
Всего-то добавили константу «а» в знаменатель. Добавление какого-то числа в знаменатель в качестве слагаемого к х означает перенос всей «гиперболической конструкции» (вместе с вертикальной ассимптотой) на (-a) позиций вправо, если а — отрицательное число, и на (-а) позиций влево, если а — положительное число.
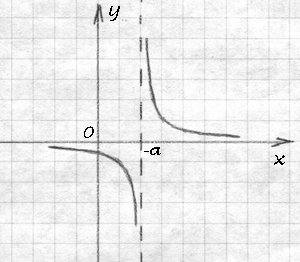
На левом графике к х добавляется отрицательная константа (а 0), что вызывает перенос графика вправо, а на правом графике — положительная константа (a>0), благодаря которой график переносится влево.
А какая магия может повлиять на перенос «гиперболической конструкции» вверх или вниз? Добавление константы-слагаемой к дроби.
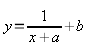
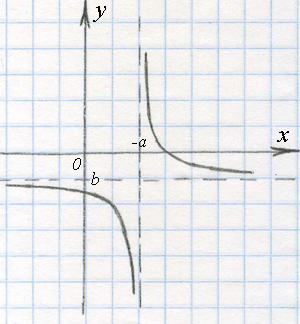
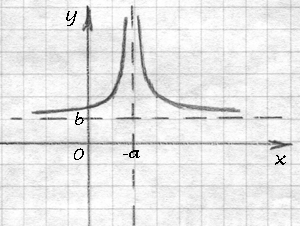
(3)
Вот теперь вся наша функция (обе веточки и горизонтальная ассимптота) поднимется на b позиций вверх, если b — положительное число, и опустится на b позиций вниз, если b — отрицательное число.
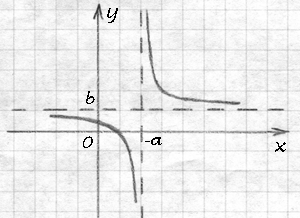
Обратите внимание, что ассимптоты передвигаются вместе с гиперболой, т.е. гиперболу (обе её ветки) и обе её ассимптоты надо обязательно рассматривать как неразрывную конструкцию, которая едино передвигается влево, вправо, вверх или вниз. Очень приятное ощущение, когда одним добавлением какого-то числа можно заставлять функцию целиком двигаться в любую сторону. Чем не магия, овладеть которой можно очень легко и направлять её по своему усмотрению в нужную сторону?
Кстати, так управлять можно движением любой функции. На следующих уроках мы это умение будем закреплять.
Перед тем как задать вам домашнее задание, я хочу обратить ваше внимание ещё вот на такую функцию
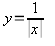
(4)
Нижняя веточка гиперболы перемещается из 3-го координатного угла вверх — во второй, в тот угол, где значение у положительное, т.е. эта веточка отражается симметрично относительно оси ОХ. И теперь мы получаем чётную функцию.
Что значит «чётная функция»? Функция называется чётной, если выполняется условие: f(-x)=f(x)
Функция называется нечётной, если выполняется условие: f(-x)=-f(x)
В нашем случае
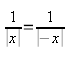
(5)
Всякая чётная функция симметрична относительно оси OY, т.е. пергамент с рисунком графика можно сложить по оси OY, и две части графика точно совпадут друг с другом.
Как видим, эта функция тоже имеет две ассимптоты — горизонтальную и вертикальную. В отличие от рассмотренных выше функций, эта функция является на одной своей части возрастающей, на другой — убывающей.
Попробуем поруководить теперь этим графиком, прибавляя константы.
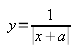
(6)
Вспомним, что прибавление константы в качестве слагаемого к «х» вызывает перемещение всего графика (вместе с вертикальной ассимптотой) по горизонтали, вдоль горизонтальной ассимптоты (влево или вправо в зависимости от знака этой константы).
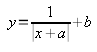
(7)
А добавление константы b в качестве слагаемого к дроби вызывает перемещение графика вверх или вниз. Всё очень просто!
А теперь попробуйте сами поэкспериментировать с такой магией.
Домашнее задание 1.
Каждый берёт для своих экспериментов две функции: (3) и (7).
а=первой цифре вашего ЛД
b=второй цифре вашего ЛД
Попробуйте добраться до магии этих функций, начиная с простейшей гиперболы, как я это делала на уроке, и постепенно добавляя свои константы. Функцию (7) уже можете моделировать, исходя из конечного вида функции (3). Укажите области определения, множество значений, ассимптоты. Как ведут себя функции: убывают, возрастают. Чётные — нечётные. В общем, попробуйте провести такое же исследование, как было на уроке. Возможно, вы найдете что-то ещё, о чём я забыла рассказать.
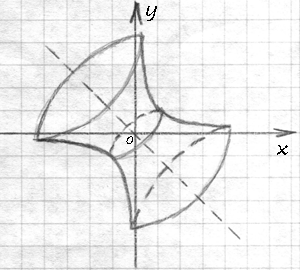
Кстати, обе ветки самой простейшей гиперболы (1) симметричны относительно биссектрисы 2 и 4 координатных углов. А теперь представьте, что гипербола стала вращаться вокруг этой оси. Получим вот такую симпатичную фигуру, которой можно найти применение.
Задание 2. Где можно использовать данную фигуру? Попробуйте нарисовать фигуру вращения для функции (4) относительно её оси симметрии и порассуждайте, где такая фигура может найти применение.
Помните, как мы в конце прошлого урока получили прямую с выколотой точкой? И вот последнее задание 3.
Построить график вот такой функции:
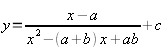
(8)
Коэффициенты a, b — такие же, как в задании 1.
с=третьей цифре вашего ЛД или a-b, если ваше ЛД двузначное.
Небольшая подсказка: сначала полученную после подстановки цифр дробь надо упростить, и затем вы получите обычную гиперболу, которую и надо построить, но в конце надо учесть область определения исходного выражения.
Отправляйте работы через ЛИЧНЫЙ КАБИНЕТ
Свои вопросы смело можете передать с Персефоной
Гипербола. График функции и свойства.
теория по математике 📈 функции
Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
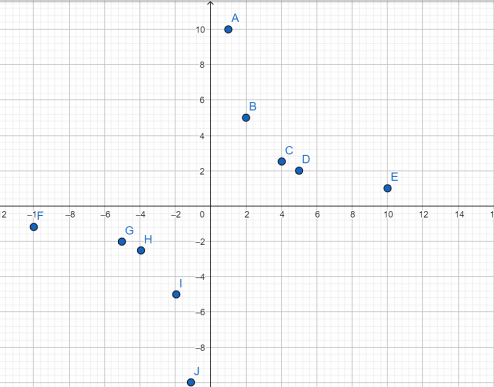
Установите соответствие между графиками функций и формулами, которые их задают.

Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Гипербола: определение, функция, формула, примеры построения
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Пример 1
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>