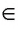Как записать что прямые пересекаются в точке

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

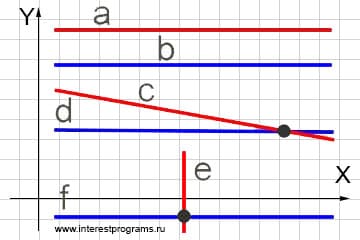
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

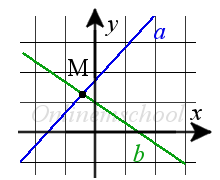
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

На уроках математики в предыдущих классах и в главе 1 вы уже познакомились со свойствами некоторых геометрических фигур. Теперь вы приступаете к систематическому изучению геометрии.

Как уже отмечалось ранее, основными геометрическими фигурами являются точка, прямая, плоскость. Представление об этих фигурах вы уже имеете.

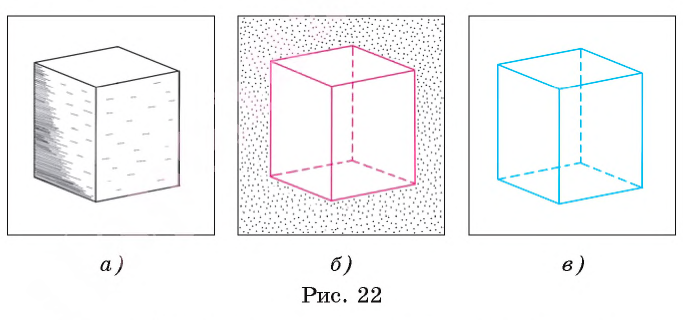
Например, туго натянутая нить дает представление о части прямой, страница книги или грань прямоугольного параллелепипеда — о части плоскости (рис. 22, а, б, в).

Если точка А принадлежит прямой b, то говорят, что прямая b проходит через точку А. Это записывают так: А

Если точка А не принадлежит прямой b, то говорят, что прямая b не проходит через точку А. В этом случае используется запись А 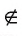b (читают: «Точка А не принадлежит прямой b», «Точка А не лежит на прямой b» или «Прямая b не проходит через точку А»).

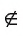
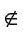
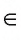
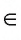
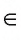
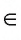
Например, на рисунке 23, а изображены точка С — вершина квадрата и точка Т, не лежащие на прямой l (С l, Т l), проходящей через вершины А и D квадрата (А l, D l). На рисунке 23, б, в изображена прямая l, проходящая через вершины О и F куба (O l, F l).

В курсе геометрии понятия « точка», « прямая» и «плоскость» относятся к основным понятиям и принимаются без определений, другие геометрические понятия определяются через основные. К основным понятиям относятся также понятия «принадлежать» и «лежать между». Свойства геометрических фигур устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств. Аксиомы выражают основные свойства геометрических фигур, которые соответствуют формам и отношениям, наблюдаемым в окружающем пространстве.

Утверждение, которое обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Доказать теорему — это значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем.

Взаимное расположение точек и прямых на плоскости характеризуют следующие основные свойства (аксиомы):

Прямая, которая проходит через точки А и В, обозначается АВ или ВА.

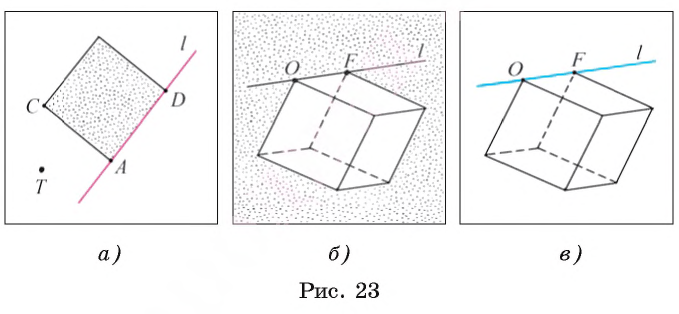
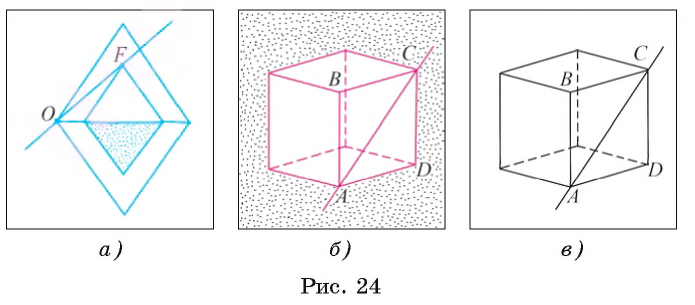
Например, на рисунке 24, а изображена прямая ОF, которая проходит через точки О и F, а на рисунке 24, б, в показана прямая АС, которая проходит через вершины А и С куба и лежит в той же плоскости, что и грань АВСD куба.

1 Здесь и в дальнейшем, говоря «две точки», «две прямые» и т. д., будем считать, что эти точки, прямые и т. д. различны.

Пересекающиеся и параллельные прямые

Рассмотрим понятия пересекающихся и параллельных прямых.

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Если прямые а и b пересекаются в точке О, то это обозначается так: О = а b (читают: «Прямые а и b пересекаются в точке О»).

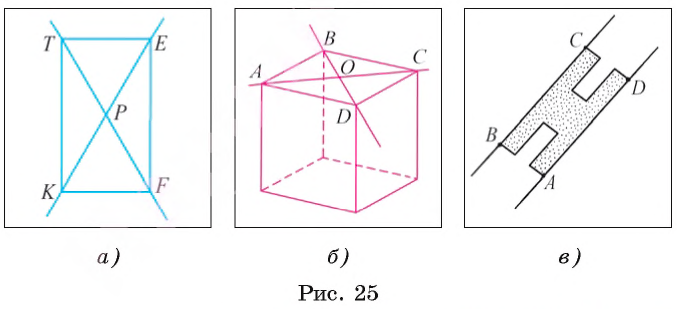
Например, на рисунке 25, а изображены прямые КЕ и TF, которые проходят через вершины прямоугольника и пересекаются в точке Р (Р =TF КЕ).

На рисунке 25, B изображены прямые АС и BD, которые проходят через вершины куба и пересекаются в точке О (О = АС 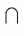ВD).

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельные прямые l₁ и l₂ обозначаются так: l₁ 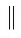l₂ (читают: «Прямая l₁ параллельна прямой l₂ »).

Например, на рисунке 25, в изображены параллельные прямые ВС и АD (ВС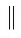АD).

Теорема. Если две прямые плоскости имеют общую точку, то она единственная.

Пусть две прямые а и b имеют общую точку О. Докажем, что других общих точек эти прямые не имеют. Допустим, что прямые а и b имеют еще одну общую точку O₁. Тогда получается, что через точки O и O₁ проходят две прямые а и b. Но этого быть не может, так как по аксиоме А3 через две точки проходит единственная прямая. Таким образом, наше предположение неверно, и прямые а и b имеют единственную общую точку.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

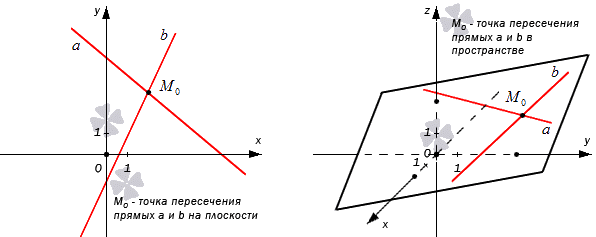
Точка пересечения двух прямых – определение

Необходимо дать определение точкам пересечения двух прямых.

Определение точки пересечения прямых звучит так:

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

Рассмотрим на рисунке, приведенном ниже.

Нахождение координат точки пересечения двух прямых на плоскости

Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что

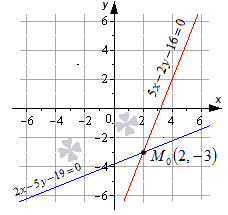
Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.

Получившиеся числа являются координатами, которые необходимо было найти.

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

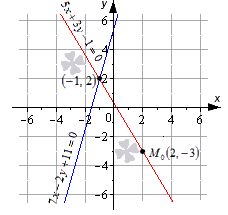
Отсюда имеем, что координаты – это точка пересечения

Применим метод Крамера для нахождения координат:

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Следует собрать уравнения в систему для последующего решения:

Ответ: заданные уравнения определяют одну и ту же прямую.

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

Ответ: точек пересечения нет, прямые параллельны.

Для решения составляем систему уравнений. Получаем

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0

Рассмотрим подобные задания на примерах.

Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

Источник

Пересечение прямых. Точка пересечения двух прямых

Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.

Точка пересечения двух прямых на плоскости

Если система уравнений:

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Вычтем из первого уравнения второе

Из первого уравнения найдем значение x

Подставим значение x во второе уравнение и найдем значение y

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

В первое уравнение подставим значения x и y из второго и третьего уравнений.

Подставим значение t во второе и третье уравнение

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Из второго уравнения выразим y через x

Подставим y в первое уравнение

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k ₁ = k ₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

Вычтем из первого уравнения второе

Ответ. Прямые не пересекаются (прямые параллельны).

Решение: Подставим координаты точки N в уравнения прямых.

Точка пересечения двух прямых в пространстве

Если система уравнений:

Решение: Составим систему уравнений

К шестому уравнению добавим пятое уравнение

Подставим значение b в четвертое и пятое уравнения

x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

Подставим значение t из шестого уравнения в остальные уравнения

Источник

Точка пересечения двух прямых на плоскости

Пересечение прямых

Для создания компьютерных игр, программ математических графиков, расчетов движения объектов и т.п. очень часто требуется найти точку пресечения прямых. Сначала необходимо на бумаге вывести и упростить формулы вычисления и далее эти формулы перевести в программный код.

Прямые это бесконечные линии, поэтому на плоскости они всегда пересекаются. Если прямые не пересекаются значит они параллельны. Частные случаи поведения прямых на плоскости: прямые неопределенны, прямые параллельны, прямые совпадают, одна из прямых параллельна оси X или Y. Общие случаи «нормального» пересечения прямых и частные случаи учитываются в программном коде класса Intersections прикрепленного исходника.

Прямые пересекаются

Даны две прямые AB и CD расположенные на одной плоскости. Они пересекаются и необходимо найти точку пересечения. За основу берем классическое уравнение прямой и подставляя данные получаем систему уравнений для двух прямых.

Классическое уравнение прямой: Запишем уравнение в одну строчку: Вычислим коэффициенты и свободные члены: В итоге получаем уравнение прямой с коэффициентами:

Уравнение с линейными коэффициентами отличается от уравнения с угловым коэффициентом отсутствием операции деления. Минимум операций деления упрощает создание устойчивого программного кода.

Точка пересечения прямых

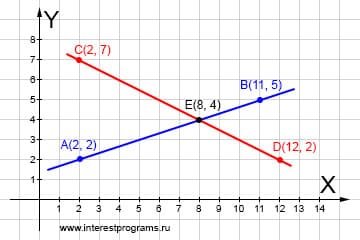
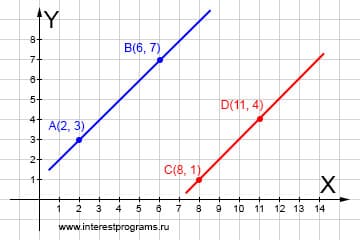
Координаты точки пересечения это числа которые являются решением для каждого из уравнений прямых. Решая систему из двух уравнений находим в какой точке пересекаются прямые AB и CD.

Подставляем известные данные: Получаем два уравнения: Решаем систему уравнений: Найдено, прямые пересекаются в точке с координатами:

Прямые параллельны

Если прямые параллельны и лежат друг от друга на расстоянии, то у них нет общих точек. Совместная система уравнений не имеет решений. Эти уравнения существуют как бы сами по себе. В точности как их параллельные прямые.

Две прямые могут полностью совпадать, в таком случае у них бесконечное количество общих точек. Совпадение прямых означает равность коэффициентов и свободных членов уравнений. Совпадающие прямые имеют идентичные уравнения.

Применяя формулу у.2 выведем уравнения прямых: Получаем систему уравнений:

Итог: система уравнений параллельных прямых не имеет решений.

Уравнение в программный код

На бумаге всё славненько, надо также сделать и в программном коде. Но программы не разбираются в уравнениях, им подавай переменные, постоянные и функции. Программный код не терпит неопределенности, он требует точные данные. Очень желательно строить выражения без операций деления. Преобразуем в программный код уравнение с коэффициентами (у.3) описанное выше. Для каждой прямой своё уравнение и переменные.

Точки определяющие прямые запишем в структуры Point. У каждой прямой две точки и они являются входными данными:
Определяем коэффициенты и свободные члены уравнений. Записываем их в соответствующие переменные:
Точка пересечения также будет храниться в структуре Point:

Вывод результата

Проверка параллельности и совпадения

Проверка на перпендикулярность

Класс Intersections

Исходник представляет собой два класса: класс вычисления точки пересечения прямых и информационный класс выдающий множество дополнительных сведений о свойствах исследуемых прямых.

Краткий листинг исходника дающий представление о структуре классов:

Применение класса Intersections

Класс class Intersections легко встраивается в любой исходный код. Точки определяющие прямые являются входными данными. На выходе получаем результат пересечения, координаты точки пересечения. Для дальнейшей обработки результатов можно использовать идентификатор свойства пересечения и дополнительную текстовую информацию.

Прикрепленный файл

Скачать исходник

Похожая тематика

Источник