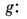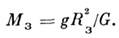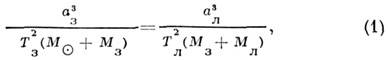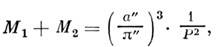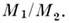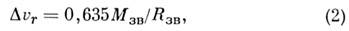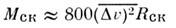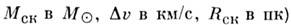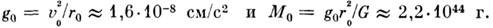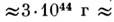Масса в астрономии в чем измеряется

МАССЫ НЕБЕСНЫХ ТЕЛ

(методы определения). В основе определения M. н. т. лежит всемирного тяготения закон. В астрономии часто (но не всегда) можно пренебречь размерами небесных тел по сравнению с разделяющими их расстояниями и отличием их формы от точной сферы, т. е. уподобить небесные тела точечным массам.

Масса Земли может быть определена по величине ускорения свободного падения

г. Более точно M 3 (вернее, произведение GMз )определяется по наблюдениям ИСЗ или космич. аппаратов. Помимо массы Земли, прямым гравиметрич. методом измерения силы тяжести на поверхности небесного тела можно определить массу Луны, а в дальнейшем всех планет и их спутников с твёрдой поверхностью.

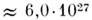
Массу Солнца 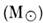можно определить, применив 3-й

закон Кеплера к движению Земли (вместе с Луной) вокруг Солнца и к движению Луны вокруг Земли:

где а— большие полуоси орбит, T— периоды (звёздные, или сидерические) обращения. Если пренебречь массой Земли по сравнению с массой Солнца, то отношение 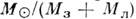оказывается равным 329390, отсюда

Ф-ла (1) даёт возможность сравнить массы Солнца и любой планеты, имеющей спутник, или массы двух планет, имеющих спутники. Массы планет, у к-рых нет спутников, определяют по возмущениям, оказываемым ими на движение соседних планет.

Массу звезды (помимо Солнца) можно определить со сравнительно большой надёжностью только в том случае, если она является физ. компонентом визуально-двойной звезды (см. Двойные звёзды), расстояние до к-рой известно. 3-й закон Кеплера в этом случае

даёт сумму масс компонентов (в единицах солнечной массы):

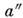
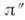
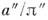
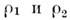
где — большая полуось (в секундах дуги) относительной орбиты спутника вокруг главной (обычно более яркой) звезды, к-рую в этом случае считают неподвижной; P— период обращения в годах;— параллакс системы (в секундах дуги). Величина даёт значение большой полуоси орбиты в а. е. Если можно измерить угл. расстояния компонентов

от общего центра масс [напр., по положению каждого компонента относительно несколько более слабых звёзд (звёзд фона) или в случае заметного собств. движения центра масс, как у Сириуса и его спутника], то находят отношение масс, 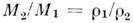, и, следо-

вательно, массу каждой звезды в отдельности.

Для определения малых значений 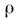у тесных двойных звёзд успешно применяются методы спекл-интер-ферометрии. Если компоненты двойной имеют примерно одинаковый блеск и сходные спектры, то полусумма масс даёт достаточно надёжную оценку массы каждого компонента и без дополнит, определения отношения

Для др. типов двойных звёзд (затменно-двойных и спектрально-двойных) имеется ряд возможностей приблизительно определить массы звёзд или оценить их ниж. предел.

Совокупность данных о массах компонентов более чем сотни двойных звезд разных типов позволила обнаружить важную статистич. масса— светимость зависимость. На основе этой зависимости оценивают массы одиночных звёзд по их светимостям.

Ещё один метод оценки массы звезды связан с измерением гравитац. красного смещения спектральных линий в поле тяготения. В сферически симметричном поле тяготения звезды оно эквивалентно доплеровскому красному смещению:

У т. н. астрометрич. двойных звёзд один компонент невидим. Массу невидимого (тёмного) спутника звезды можно оценить по колебаниям положения звезды, связанным с её движением около общего центра масс. Невидимые спутники звёзд имеют массы меньше 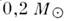и, вероятно, похожи на планеты. Возможно, что вместо одного тёмного спутника имеются два-три, а может быть, и большее число спутников (планет), т. е. планетные системы.

На релятивистском эффекте вращения линии апсид орбиты звезды-компаньона (подобного эффекту вращения линии апсид планетарных орбит, см. Тяготение )основан ещё один способ определения масс компонентов двойной звезды.

Массы звёзд заключены в пределах прибл. от 0,03 до 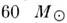(теоретич. предел стабильной массы нор-

мальной звезды 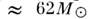). Наиб, число звёзд имеет

массы от 0,3 до 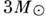, много более половины звёзд вхо-

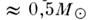
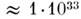
дят в двойные системы. Cp. масса звезды в ближайших окрестностях Солнца , т. е.г. Разли-

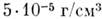
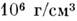
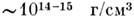
чие в массах звёзд оказывается много меньшим, чем их различие в светимостях (последнее может достигать десятков млн.). Сильно отличаются радиусы звёзд. В результате диапазон их ср. плотностей от (красные гиганты) до (белые карлики) и даже

(нейтронные звёзды). Cp. плотность Солнца равна

Массу шарового звёздного скопления М ск далеко не всегда можно оценить путём подсчёта звёзд, т. к. изображения звёзд центр, области большинства шаровых скоплений на фотографиях, полученных с оптим. экспозицией, сливаются в одно светящееся пятно. Есть методы оценки общей массы всего скопления, основанные на статистич. принципах. Так, напр., применение вириала теоремы позволяет оценить М ск по эфф. радиусу скопления R cк и ср. квадрату отклонения 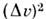лучевой скорости отд. звёзд от её ср. значения (т. е. от лучевой скорости скопления как целого):

(здесь

где сумма взята от самых ярких до самых слабых членов скопления.

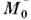
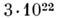
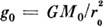
Метод определения массы Галактики М г . использует факт вращения Галактики. Устойчивость вращения позволяет предположить, в частности, что центро-стремит. ускорение Солнца определяется притяжением массы всего вещества Галактики внутри сферы с радиусом , где — расстояние Солнца от центра Галактики, равное прибл. см. Cp. гравитац. ускорение Солнца равно его центростре-мит. ускорению (без учёта влияния внеш. части Галактики и при условии эллипсоидальности поверхностей равной плотности в её внутр. части). Собств. галактич. скорость Солнца (т. н. круговая скорость на расстоянии r 0 от центра) v 0

Масса Галактики в сферич. объёме радиусом

15 кпк, как показывают подобные расчёты, равна

. При этом учитывается также масса всей диффузной (рассеянной) материи в Галактике.

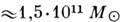
Масса спиральной галактики может быть определена по результатам изучения её кривой вращения (см. Вращение галактик). Кривые вращения указывают на наличие больших масс невидимого (несветящегося) вещества (т. н. скрытой массы). Масса невидимого вещества галактик может в 10 раз и более превосходить массу светящегося (излучающего) вещества.

Для медленно вращающихся галактик, какими являются, напр., эллиптич. галактики, трудно получить кривую вращения, но зато можно по расширению спектральных линий оценить дисперсию скоростей звёзд в системе и, сопоставив её с истинными размерами галактики, по теореме о вириале оценить массу эллиптич. галактики.

интегральной звёздной величине галактики и расстоянию до неё, оценённому по величине красного смещения спектральных линий.

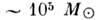
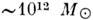
Известные ныне массы галактик заключены в пределах от — для т. н. карликовых галактик до — для сверхгигантских эллиптич. галактик (напр., для галактики М87).

Общая масса галактик, входящих в скопления галактик, определяется суммированием масс галактик данного скопления с учётом их типов. С др. стороны, полная масса скопления может быть определена по теореме о вириале (по дисперсии лучевых скоростей галактик в скоплении в предположении, что галактики скопления являются гравитационно связанными между собой). Подобные определения показывают, что полная масса скопления (её наз. вириальной массой) больше суммы масс отд. галактик скопления. Это свидетельствует о том, что в межгалактич. пространстве в скоплениях содержится много невидимой (скрытой) массы. Сверхскопление галактик с центром в созвездии Девы обладает суммарной массой

Точность определения M. н. т. зависит от точности определения всех величин, входящих в соответствующие Формулы. Масса Земли найдена с погрешностью

Лит.:Cагитов M. У., Постоянная тяготения и масса Земли, M., 1969; Физика космоса. Маленькая энциклопедия, 2 изд., M., 1986; Куликовский П. Г., Звёздная астрономия, 2 изд., M., 1985; Климишин И. А., Открытие Вселенной, M., 1987. Я. Г. Куликовский.

Источник

Как измеряют массу планет

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Планеты солнечной системы

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

Похожие статьи

Понравилась запись? Расскажи о ней друзьям!

Источник

uCrazy.ru

Навигация

ЛУЧШЕЕ ЗА НЕДЕЛЮ

ОПРОС

СЕЙЧАС НА САЙТЕ

КАЛЕНДАРЬ

Сегодня день рождения

Рекомендуем

Как ученые измерили массу Земли и других планет?

Планета – объект большой, его на весы не поставишь. Как же ученым удалось узнать массу Земли? Как измеряется масса далеких космических объектов?

Существует 2 способа определения массы Земли: с помощью барометра и математических вычислений, или анализа частиц нейтрино.

Барометр и законы Ньютона

Метод, применяемый с XVIII века. Для расчета используются второй закон Ньютона (F=mg) и закон всемирного тяготения (F=G*m*M/R^2).

F – это сила земного притяжения барометра, G – коэффициент гравитационной постоянной, R – радиус планеты, m – вес прибора, M – вес планеты.

Отдельно масса Земли вычисляется по формуле: M = g*R^2/G, где g – это ускорение свободного падения.

Ускорение свободного падения узнали, сбросив барометр с высокой башни и измерив время, которое он пролетел до столкновения с землей. Выяснилось, что за каждую последующую секунду барометр преодолевал почти 9.8 метров. Таким образом, g = 9.8 м/с².

Радиус Земли был известен еще с Античности. Столь сенсационное открытие сделал греческий математик Эратосфен в III веке до н.э.

Ученый подождал день летнего солнцестояния. В это время светило находится в самой высокой точке на небе и в 12 часов отбрасывает наименьшую тень в году.

Математик присмотрелся к обелиску, стоящему неподалеку, измерил отбрасываемую им тень, измерил сам обелиск, высчитал все углы, а потом сделал то же самое в соседнем городе. Расчеты дали ему окружность земли в 38.5 тысяч километров. Современные ученые пересчитали окружность подобным методом и высчитали 40 000 км.

Планета идеальным шаром не является, а потому ее радиус оказался 6371 км.

Труднее всего было найти коэффициент гравитационной постоянной. Для этого исследователи взяли однотонный свинцовый шар и посмотрели, с какой силой он притягивал барометр.

G = 6,67430(15)*10ˆ(-11) Н·м²·кг²

Подставив все эти цифры в уравнение, ученые высчитали, что Земля весит шесть септиллионов кг или 6^24 кг.

Это мельчайшие субатомные частицы, которые испускает Солнце. Они проходят планету насквозь.

Испанские физики поставили лабораторию на Южном полюсе, дождались момента, когда Солнце окажется на Северном полюсе и выловили нейтрино с обратной стороны.

Эксперимент кажется фантастичным, однако измерив скорость частиц, прошедших сквозь Землю, физики нашли плотность планеты и, соответственно, массу.

Как измеряются далекие планеты?

Масса далеких планет вычисляется примерно. Основами для вычислений становятся орбиты планет, орбиты их спутников и гравитационные возмущения между ними.

Масса звезд вычисляется по степени их яркости. Считается, чем ярче небесное тело, тем оно массивнее. По светимости звезды определяется её химический состав, а значит примерная плотность и вес.

Источник

Глава I. Астрофизика и методы анализа размерностей

§ 1.1 Размерности астрофизических величин

Напомним определение размерных и безразмерных величин. Величина называется размерной, или именованной, если ее численное значение зависит от выбора системы единиц измерения. Примеры: масса звезды, ее радиус, плотность и т. д. Величины называются безразмерными, если их значение сохраняется неизменным в различных системах единиц. Это угол, отношение двух длин и вообще отношение двух одноименных величин, показатель экспоненты в законе Планка (hν/kT) и т. д.

Следует сразу же отметить относительность понятия размерности. Так, в геометрии угол является величиной безразмерной (отношение двух дуг). Однако в астрономии углы измеряются в градусах, минутах и секундах дуги или в часах, минутах и секундах времени. Безразмерное отношение двух длин может выражаться в процентах и т. д. Таким образом, не только количественное значение, но и размерность физической величины может изменяться при другом выборе системы единиц измерения. Вообще размерность всегда связана с принятой системой единиц. В дальнейшем вместо полного наименования «размерность физической величины в данной системе единиц измерения» мы будем говорить просто «размерность».

Таким образом, выбор основных единиц измерения, как правило, диктуется удобствами определения величины, областью рассматриваемых проблем, историческими причинами. Например, хотя в астрофизике часто имеют дело с измерениями световых потоков, свеча в качестве основной единицы измерения почти никогда не используется, так как астрофизические потоки очень слабы. Очень редко в астрофизике в качестве основной единицы измерения используется и ампер.

для единицы энергии можно понимать и в более широком смысле, как изображающее любую систему единиц, основанную на единицах длины, массы и времени (например, системы СИ).

Обозначение [А] для характеристики размерности физической величины было предложено Максвеллом и с тех пор широко употребляется. Реже встречается обозначение [А], дающее численное значение величины A в данной системе единиц.

Размерность производной величины выражается через размерности основных величин в виде произведения степеней. Учитывая сделанный нами выбор основных первичных единиц, можно написать для размерности любой астрофизической величины:

Пн	Вт	Ср	Чт	Пт	Сб	Вс
1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

(1.1)

В астрофизике чаще всего светимость измеряют в единицах светимости Солнца L_&#9737. B наблюдательных работах пользуются безразмерной звездной величиной, пропорциональной логарифму отношений светимости:

Светимость может быть полной (болометрической) или отнесенной к определенным диапазонам спектра электромагнитного излучения.

(1.2)

т. е. из этих трех величин нельзя образовать одной безразмерной комбинации. Это означает, что эти величины можно было бы выбрать за три основные первичные единицы размерности. Подобное предположение было высказано, в частности, Д. А. Франк-Каменецким [1].

(1.3)

Вообще для астрофизических параметров характерен огромный, поистине астрономический разброс величин с одинаковой размерностью.

В современной астрофизике большую роль играют магнитные поля. В физике (в системе CGSE) различают размерности напряженности магнитного поля H и его индукции В, измеряемых в эрстедах и гауссах соответственно; в системе СИ используются единицы ампер/метр и тесла. Подобное усложнение единиц для характеристики магнитных свойств в астрофизике не необходимо, поскольку здесь магнитная проницаемость почти строго равна единице, так что единицы гаусс и эрстед совпадают. В физике для определения величин H и В обычно используют уравнения Максвелла и выражают эти величины через силу тока и ее размерность, но это неудобно для астрофизики.

Лучше всего для определения В воспользоваться тем, что плотность энергии магнитного поля равна В 2 /8π. Поэтому размерность

(1.4)

с точностью до безразмерного множителя и есть один эрстед или один гаусс в системе CGSE. В астрофизической литературе часто используют обозначение B и H для определения магнитных полей и пользуются обеими единицами. Строго говоря, правильнее использовать индукцию B и измерять поле в гауссах, что мы и будем делать в этой книге.

Источник