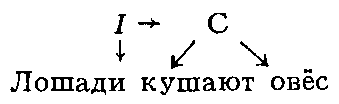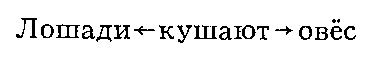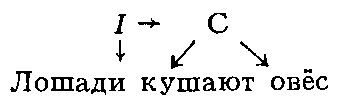Математическая лингвистика что это
Математическая лингвистика
Полезное
Смотреть что такое «Математическая лингвистика» в других словарях:
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков … Большой Энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА. Смежная для методики обучения языкам наука; раздел лингвистики, использующий математические методы исследования языка и речи. Данные М. л. применяются для проведения экспериментов в методике … Новый словарь методических терминов и понятий (теория и практика обучения языкам)
Математическая лингвистика — (также вычислительная лингвистика или компьютерная лингвистика) направление искусственного интеллекта, которое ставит своей целью использование математических моделей для описания естественных языков. Компьютерная лингвистика частично… … Википедия
математическая лингвистика — математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. * * * МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА, математическая дисциплина,… … Энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — математическая дисциплина, предметом к рой является разработка и изучение понятий, образующих основу формального аппарата для описания строения естественных языков (т. е. метаязыка лингвистики). Возникновение М. л. можно отнести приблизительно к… … Математическая энциклопедия
математическая лингвистика — 1. Изучает особенности семиотического и математического моделирования естественного языка (и речи) с целью перевода информации, содержащейся в неформализованном виде в тексте, на формализованный искусственный язык (например, на некоторый… … Толковый переводоведческий словарь
Математическая лингвистика — Математическая лингвистика математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Возникла в 50‑х гг. 20 в.; одним из главных стимулов появления… … Лингвистический энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — матем. дисциплина, предметом к рой является разработка формального аппарата для описания строения естественных и нек рых искусств, языков … Естествознание. Энциклопедический словарь
математическая лингвистика — Отрасль языкознания, занимающаяся изучением возможностей применения математических методов к изучений и описанию языка … Словарь лингвистических терминов
математическая лингвистика — Направление, возникшее в XX в. на стыке языкознания, математики и математической логики и занимающееся разработкой формального аппарата описания языка, применяемого в частности, в диалоге человек – ЭВМ … Словарь лингвистических терминов Т.В. Жеребило
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
Таким образом, можно выделить три аспекта формального описания языка: описание строения языковых объектов различных уровней, описание нек-рых специальных отношений и классификаций на множествах этих объектов и описание преобразований одних объектов в другие, а также строения множеств «правильных» объектов. Этим аспектам отвечают три основных раздела М. л.: 1) разработка и изучение способов описания строения отрезков речи; 2) изучение лингвистически значимых отношений и классификаций на множествах языковых объектов (построенные для этой цели формальные системы обычно называют аналитическими моделями языка);3) теория формальных грамматик.
Для описания строения отрезков речи используются синтаксич. структуры, представляющие собой графы или биграфы специального вида, обычно с помеченными вершинами и/или дугами. Лучше всего разработана теория описания «поверхностных» уровней (т. е. наиболее далеких от «смыслового»); на этих уровнях структуры обычно являются деревьями. Интенсивно разрабатываются способы описания более «глубинных» уровней. Для этого, в частности, предложен аппарат т. н. лексических функций, играющих при описании смысловой сочетаемости слов роль, сходную с той, к-рую традиционные категории рода, падежа, числа и т. п. играют при описании синтаксич. сочетаемости. Средств строгого описания «смыслового» уровня пока нет, но многим исследователям представляется вероятным, что на таком пути «последовательного приближения» можно надеяться выработать подход к формальному описанию смысла. Это не исключает и иных подходов; в частности, много исследований посвящено способам выражения в естественных языках предикатов, пропозициональных связок, кванторов, «переводу» с формально-логич. языков на естественные и обратно. Сюда же примыкают работы по конструированию так наз. семантических языков, в к-рых смыслы сопоставляются текстам простыми и строго формальными способами.
Аналитич. модели языка важны, в частности, ввиду того, что они позволяют уточнить логич. природу многих понятий и категорий традиционного языковедения. Эти модели не всегда носят характер эффективных процедур, поскольку в них могут входить такие понятия, как (бесконечное) множество грамматически правильных предложений нек-рого языка, считающееся заданным. Однако в ряде моделей все исходные данные представляют собой конечные множества и финитные отношения; в этих случаях входящие в модель процедуры эффективны. К теории аналитич. моделей языка примыкает теория лингвистической д е ш и ф р о в к и: ее предметом является построение процедур, применяемых, подобно аналитич. моделям, к «неупорядоченным» эмпирич. данным о языке, но всегда эффективных и позволяющих получать не только абстрактные определения, но и конкретные сведения о строении конкретных языков (напр., алгоритмы, осуществляющие автоматич. разбиение множества фонем языка на классы гласных и согласных без использования каких-либо сведений о языке, кроме нек-рого достаточно длинного текста).
Теория формальных грамматик наряду с «традиционными» для нее лингвистич. приложениями нашла применение в теории программирования для описания языков программирования и трансляторов. Особенно широко применяются для этих целей бесконтекстные грамматики, но используются и грамматики более общего вида.
Лит.:[1] Xомский Н., в кн.: Новое в лингвистике, в. 2, М., 1962, с. 412-527; [2] Гладкий А. В., Мельчук И. А., Элементы математической лингвистики, М., 1969.
Математическая лингвистика
Математическая дисциплина, разрабатывающая формальный аппарат для описания строения естественных и некоторых искусственных языков. Возникла в 50-х годах 20 века в связи с назревшей в языкознании потребностью уточнения его основных понятий. В М. л. используются по преимуществу идеи и методы алгебры, алгоритмов теории (См. Алгоритмов теория) и автоматов теории (См. Автоматов теория). Не являясь частью лингвистики, М. л. развивается в тесном взаимодействии с ней. М. л. называют иногда лингвистические исследования, в которых применяется какой-либо математический аппарат.
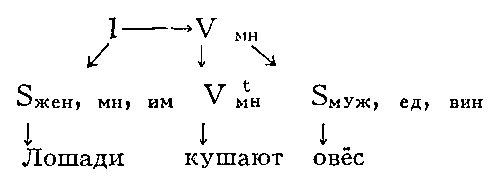
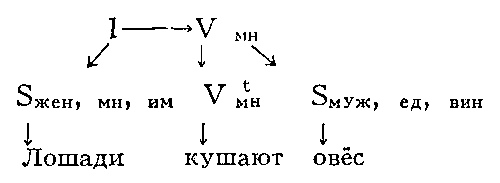
Математическое описание языка основано на восходящем к Ф. де Соссюру представлении о языке как механизме, функционирование которого проявляется в речевой деятельности его носителей; её результатом являются «правильные тексты» — последовательности речевых единиц, подчиняющиеся определённым закономерностям, многие из которых допускают математическое описание. Изучение способов математического описания правильных текстов (в первую очередь предложений) составляет содержание одного из разделов М. л. — теории способов описания синтаксической структуры. Для описания строения (синтаксической структуры) предложения можно либо выделить в нём «составляющие» — группы слов, функционирующие как цельные синтаксические единицы, либо указать для каждого сло́ва те слова́, которые от него непосредственно зависят (если такие есть). Так, в предложении «Лошади кушают овёс» при описании по 1-му способу составляющими будут: всё предложение I, каждое отдельное слово и словосочетание С = «кушают овёс» (рис. 1; стрелки означают «непосредственное вложение»); описание по 2-му способу даёт схему, показанную на рисунке 2. Математические объекты, возникающие при таком описании структуры предложения, называются деревом составляющих (1-й способ) и деревом синтаксического подчинения (2-й способ).
М. л. изучает также аналитические модели языка, в которых на основе тех или иных данных о речи, считающихся известными (например, множества правильных предложений), производятся формальные построения, дающие некоторые сведения о структуре языка. Приложение методов М. л. к конкретным языкам относится к области лингвистики (см. Языкознание).
Лит.: Хомский Н., Синтаксические структуры, в сборнике: Новое в лингвистике, в. 2, М., 1962; Гладкий А. В.. Мельчук И. А., Элементы математической лингвистики, М., 1969; Маркус С., Теоретико-множественные модели языков, перевод с английского, М., 1970; Гладкий А. В., Формальные грамматики и языки, М., 1973.
Рис. 1 к ст. Математическая лингвистика.
Рис. 2 к ст. Математическая лингвистика.
Рис. 3 к ст. Математическая лингвистика.
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
Смотреть что такое «МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА» в других словарях:
Математическая лингвистика — математическая дисциплина, разрабатывающая формальный аппарат для описания строения естественных и некоторых искусственных языков. Возникла в 50 х годах 20 века в связи с назревшей в языкознании потребностью уточнения его основных понятий … Большая советская энциклопедия
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков … Большой Энциклопедический словарь
Математическая лингвистика — (также вычислительная лингвистика или компьютерная лингвистика) направление искусственного интеллекта, которое ставит своей целью использование математических моделей для описания естественных языков. Компьютерная лингвистика частично… … Википедия
математическая лингвистика — математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. * * * МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА, математическая дисциплина,… … Энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — математическая дисциплина, предметом к рой является разработка и изучение понятий, образующих основу формального аппарата для описания строения естественных языков (т. е. метаязыка лингвистики). Возникновение М. л. можно отнести приблизительно к… … Математическая энциклопедия
математическая лингвистика — 1. Изучает особенности семиотического и математического моделирования естественного языка (и речи) с целью перевода информации, содержащейся в неформализованном виде в тексте, на формализованный искусственный язык (например, на некоторый… … Толковый переводоведческий словарь
Математическая лингвистика — Математическая лингвистика математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Возникла в 50‑х гг. 20 в.; одним из главных стимулов появления… … Лингвистический энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — матем. дисциплина, предметом к рой является разработка формального аппарата для описания строения естественных и нек рых искусств, языков … Естествознание. Энциклопедический словарь
математическая лингвистика — Отрасль языкознания, занимающаяся изучением возможностей применения математических методов к изучений и описанию языка … Словарь лингвистических терминов
математическая лингвистика — Направление, возникшее в XX в. на стыке языкознания, математики и математической логики и занимающееся разработкой формального аппарата описания языка, применяемого в частности, в диалоге человек – ЭВМ … Словарь лингвистических терминов Т.В. Жеребило
Математическая лингвистика
Математи́ческая лингви́стика (также вычисли́тельная лингви́стика или компью́терная лингви́стика) — направление искусственного интеллекта, которое ставит своей целью использование математических моделей для описания естественных языков.
Компьютерная лингвистика частично пересекается с обработкой естественных языков. Однако в последней акцент делается не на абстрактные модели, а на прикладные методы описания и обработки языка для компьютерных систем.
Содержание
Истоки
Математическая лингвистика является ветвью науки искусственного интеллекта. Всё началось в Соединённых Штатах Америки, в 1950-х годах. С изобретением транзистора и появлением нового поколения компьютеров, а также первых языков программирования, начались эксперименты с машинным переводом, особенно русских научных журналов. В 1960-х годах подобные исследования проводились и в СССР (например, статья о переводе с русского на армянский в сб. «Проблемы кибернетики» за 1964 год). Однако качество машинного перевода до сих пор сильно уступает качеству перевода, произведённого человеком. Были созданы первые системы искусственного интеллекта, такие как SHGSL. Они, правда, устарели, но пользуются популярностью у студентов и научных сотрудников Академий Наук, занимающихся компьютерной лингвистикой.
С 15 по 21 мая 1958 г. в I МГПИИЯ состоялась первая Всесоюзная конференция по машинному переводу. Оргкомитет возглавляли В. Ю. Розенцвейг и ответственный секретарь Оргкомитета Г. В. Чернов. Полностью программа конференции опубликована в сборнике «Машинный перевод и прикладная лингвистика», вып. 1, 1959 г. (он же «Бюллетень Объединения по машинному переводу № 8»). Как вспоминает В. Ю. Розенцвейг, опубликованный сборник тезисов конференции попал в США и произвел там большое впечатление.
В апреле 1959 года в Ленинграде состоялось I Всесоюзное совещание по математической лингвистике, созванное Ленинградским университетом и комитетом прикладной лингвистики. Главным организатором Совещания был Н. Д. Андреев. В Совещании приняли участие ряд видных математиков, в частности, С. Л. Соболев, Л. В. Канторович (впоследствии — Нобелевский лауреат) и А. А. Марков (последние двое выступали в прениях). В. Ю. Розенцвейг выступил в день открытия Совещания с программным докладом «Общая лингвистическая теория перевода и математическая лингвистика».